财经类“线性代数”课程改革的几点实践性措施

苏燕玲

(对外经济贸易大学统计学院，北京100029)

随着线性代数的发展，线性代数中的基本概念及许多数学分支中的问题有了更加丰富的几何意义，一些深奥又复杂的问题可以用简洁的形式来表述，使得线性代数在各个学科及经济管理领域的应用越来越广泛。但由于线性代数具有较强的抽象性与逻辑性，很多学生感到线性代数概念难以理解，从而丧失学习线性代数的兴趣。本文结合实践性教学，阐述了财经类线性代数课程改革的一些理念和做法。

1　“线性代数”课程现状及存在问题

从生源层面来讲，绝大多数财经类院校学生是文理兼收，学生数学基础参差不齐，文科生占较大比例，他们的特点是大部分数学基础不扎实，对数学缺少兴趣，信心不足，计算能力差，演绎推理、逻辑思维欠缺；优点是形象思维发达，善于记忆，喜欢直观有用的东西，不明白学习这门课的目的，很难激发学生学习的积极性与主动性。

从教学内容看，众多的线性代数教材重理论轻应用，重公式推导轻数值计算，教材大多忽略了概念、原理和模型的实际意义。因此，不能引起学生的兴趣，使学生产生学而无用的错觉，直接影响学习效果。

从教学方法看，以往线性代数教学主要是以老师放映PPT加板书，学生记笔记为主。由于线性代数课程的特点就是抽象性、严密性，符号多、概念定理多，相对于微积分和概率论的学习显得更为抽象。加之教学过程过于强调理论推导与计算，没有或者很少与实际问题联系，很难使学生学以致用，达到提高数学应用能力的目的。

从教学效果看，通过调研，我们发现经济管理类学科越来越重视建立数学模型并进行定量分析，而目前的课程不能满足大学生的这一需求，大多数学生对该课程的反应是抽象、冗繁、枯燥、无用，在实际应用中手足无措，他们普遍认为该课程缺乏一种在学习数学的基础上用数学的能力。

2　“线性代数”课程改革的几点实践性措施

2.1　启发式教学与问题解决相结合，激发学生学习兴趣

启发式教学是针对学生的疑问或兴趣点出发而进行有意识的启发和引导的教学过程，在这个过程中始终伴随着概念产生及问题解决.在教学中，教师应针对某个实际问题，启发学生探索、思考解决问题的思路、方法，再现数学规律的发现过程，培养学生思考问题的习惯和能力，加深对概念本质的理解.在问题的解决过程中同时根据需要引入概念和定义，提供方法和技巧.比如在给出矩阵乘法之前可以给出如下实例

例1　甲、乙两厂，生产A、B、C三种产品，各厂生产各种产品的产量为

三种产品单位产量的价格与单位耗电、耗油、耗水量为

试分析甲乙两厂的总收入、总耗电量、总耗油量、总耗水量。

通过对上述实际问题的分析，甲乙两厂的总收入总耗电量、总耗油量、总耗水量可以表示为矩阵

分析其规律，顺势给出矩阵乘法定义及对相关知识进行介绍和讲解。

矩阵的特征值特征向量是线性代数中的一个重要概念，直接引入学生很难理解，通过以下实例引入学生就不会感到突兀，难以接受。

例2由于矩阵乘法对应了一个变换，把一个向量变成同维数的另一个向量，那么变换的效果是什么呢?这当然与方阵的构造密切相关，比如可以取适当的二维方阵，使得这个变换的效果就是将平面上的二维向量逆时针旋转30度，这时我们可以问一个问题，有没有向量在这个变换下不改变方向呢?引领学生思考平面上的一个变换，把一个向量关于横轴做镜像对称变换(有条件的话可以直接借助多媒体手段直接对某个名人的照片进行这个变换)，即保持一个向量的横坐标不变，但纵坐标取相反数，把这个变换表示为矩阵就是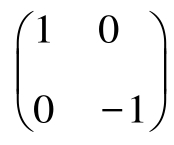，显然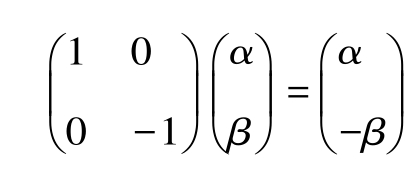，这正是我们想要的效果，那么现在可以猜一下了，这个矩阵的特征向量是什么?想想什么向量在这个变换下保持方向不变，显然，横轴上的向量在这个变换下保持方向不变，所以可以直接猜测其特征向量是(α≠ 0)。由此揭开特征值特征向量的神秘面纱，让学生认识到特征值特征向量就在我们身边，特征值只不过反映了特征向量在变换时的伸缩倍数，特征向量指明的是变换后的方向。

这种通过对各种实际现象的观察、分析和归纳而发现问题、研究问题、解决问题，透过现象抓本质，再现了科学探索和科学发现的过程，有利于激发学生的学习和研究兴趣。

2.2　以学生为主体，调动学生学习积极性

改变传统的以教师单一讲授为主的教学方法，采用以学生为主体、教师为主导的讨论法。其优点是通过教师引导学生自学，提出问题，启迪学生积极思维，经过质疑和答疑来解决问题，使学生的主体作用充分发挥，在此基础上还可以结合讲授法，将重点、难点讲清、讲透，从而调动学生学习的积极性。所以在平时的教学中要特别注重学生的主体性，合理设置教学典型实例，调动学生学习积极性。比如学习伴随矩阵时，大家得到二阶矩阵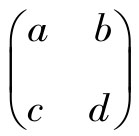的伴随矩阵是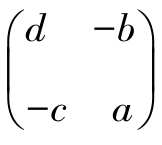，让学生观察有没有规律.学生思考后发现求二阶矩阵的伴随阵只需要把主对角线上的两个元素交换位置，副对角线上的元素位置不变添个负号即可。学习矩阵乘法时，令矩阵A与B是A=(123)_1×3，B=，让学生分别计算AB与BA(www.daowen.com)

AB=(123)_1×3=(14)_1×1= 14，BA=(123)_1×3= 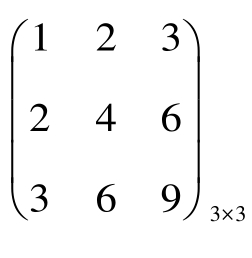通过结果学生发现显然AB≠BA，即矩阵乘法不满足交换律。经过这样的典型实例分析，学生自己也可以总结出书上没有的结论，感觉无比自豪，极大地提高了学生的学习热情，培养了他们的创新精神。

2.3　通过应用案例，灌输数学建模思想，培养学生解决实际问题能力

对于财经类院校的很多学生，特别是一些文科生，面对实际问题时常常手足无措，甚至对摆在眼前的线性代数问题视而不见，针对这种情况，教师在教学中适当增加和专业实际相结合的应用案例，培养学生整理问题、分析问题、解决问题的能力，对以后的学习或工作需要打下基础。比如某金融机构为保证现金充分支付，设立一笔总额5 400万的基金，分开放置在位于A城和B城的两家公司，基金在平时可以使用，但每周末结算时必须确保总额仍然为5 400万.经过相当长的一段时期的现金流动，发现每过一周，各公司的支付基金在流通过程中多数还留在自己的公司内，而A城公司有10%支付基金流动到B城公司，B城公司则有12%支付基金流动到A城公司.起初A城公司基金为2 600万，B城公司基金为2 800万.按此规律，两公司支付基金数额变化趋势如何?如果金融专家认为每个公司的支付基金不能少于2 200万，那么是否需要在必要时调动基金?

模型分析：设第k+1周末结算时，A城公司B城公司的支付基金数分别为a_k+1，b_k+1(单位：万元)，则有a₀= 2 600，b₀= 2 800，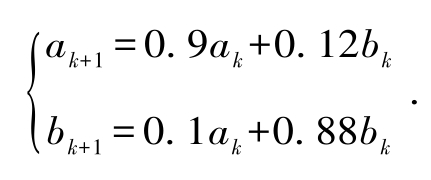

原问题转化为：

(1)把a_k+1，b_k+1表示成k的函数，并确定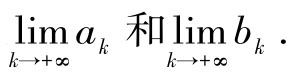

(2)看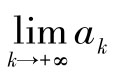和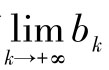是否小于2 200.

模型求解：由可得

令，则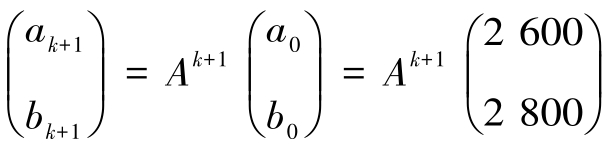.只须计算A^k+1即可。

通过该实例，一方面让学生掌握了线性代数的知识点，又让学生明白线性代数在专业中的应用。

2.4　结合MATLAB数学软件，优化教学内容

线性代数是一门应用性很强，但在理论上又高度抽象的数学学科。如何让学生特别是财经类院校的学生真正理解，掌握这门课程，并学会如何应用这门课程的理论方法解决实际问题，达到学以致用的目的，结合MATLAB数学软件，是一种很好的尝试，2009年我校参加了教育部“用MATLAB和建模实践改造线性代数课程”项目，该课题带动17所高校进行线性代数课程的改革，起到了很好的示范效应。结合MATLAB这种数学软件，既能图形并茂既能给出概念的直观意义，又能解决繁琐计算。

比如一些重要概念的引入，包括二、三阶行列式，矩阵的运算，线性变换，向量空间与子空间，基变换与坐标变换，特征值特征向量等.结合MATLAB数学软件，从几何图形入手，图形并茂阐述问题，提高了学生的感性认识。一些重要的计算也可以通过MATLAB快速实现，包括线性方程组求解、矩阵的运算、特征值和特征向量的计算、矩阵的对角化等。这些内容都可以适时加入到教学内容，通过上机教学实践，使学生学会用计算机代替笔算解题，上机做实验培养技能和乐趣，感受到数学不再枯燥及“用数学”的乐趣。同时对学生科学计算能力的培养起到很好的奠基作用。因此适当减少理论教学内容，以问题驱动，增加实例分析和计算机软件应用，将理论与实践相结合，将抽象思维训练与动手能力相结合将是我国深入线性代数教学改革的一个方向。

参考文献

[1]陈怀琛.论工科线性代数的现代化与大众化.高等数学研究，2012(2).

[2]陈怀琛.线性代数中矩阵的应用典型案例.兰州大学学报(自然科学版)，2009(45).

[3]黄玉梅.非数学专业线性代数实践性教学研究.西南师范大学学报(自然科学版)，2010(35).

[4]张鹏鸽，高淑萍，马建荣.对比国外优秀教材探索我国线性代数课程改革的新思路.大学数，2010(10).

[5]章树玲，翟丽丽，侯玉双.基于MATLAB的《线性代数》.教学方法改革研究，2013(1).

[6]龚德恩.经济数学基础第二分册线性基础.四川人民出版社，2005(7).