李　勇

高三数学复习课的实效性，是高中数学教学的一个重要话题。本文结合笔者三年来参加成都市区县名师工作室及高三教学经验谈一谈自己的看法。

一、对教材例题习题的回看和挖掘

立足教材是全国各地高考命题的一个基本原则，在高三一轮复习时，教师要全面挖掘教材例题、习题的教学功能，有选择性地对优秀试题从各个角度细细研究，将知识的外延和内涵搞清楚，不但能让学生知道并掌握各种考试的命题风格、命题热点、命题形式，而且有利于提高章节复习的针对性和实效性。

例如数学必修4第22页B组第3题：已知tana=2，计算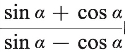的值。改编为：已知tanα=2，计算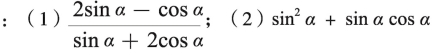

解：（1）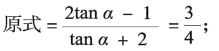

（2）

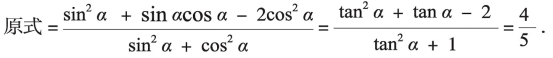
这样的改编将同角三角函数公式的应用从解决正余弦的一次齐次式推广到了二次齐次式，其中改编题的（2）问还巧妙地运用了平方关系。

二、让学生走在前面，收集问题

埃德加·富尔在《学会生存》一书中指出：“未来的文盲不再是不识字的人，而是没有学会怎样学习的人。”“教会学生学习”已成为当今世界流行的口号。就是说，学生不能只被动接受学习内容，还要敢于走在教师的前面，从教材出发，结合教辅资料，自我收集整理一些与上课板块相关联的习题，并进行分类总结，预检、分析自己的掌握情况，这样可以最大限度地调动学生学习的主动性和积极性，激发学生的思维，帮助学生掌握学习方法，培养学生的学习能力，为学生发挥自己的聪明才智提供和创造必要的条件。

如在复习数列通项公式一堂课前，学生收集了很多类似题目。

例1.等差数列｛an｝是递增数列，前n项和为Sn，且a1，a3，a9成等比数列，求数列{an｝的通项公式。

例2.已知Sn为数列｛an｝的前n项和，求下列数列｛an｝的通项公式：（1）Sn=2n2+3n-1；（2）Sn=2n1.

例3.正项数列{an｝的前n项和为Sn，且求数列｛an｝的通项公式。

例4.已知数列｛an｝满足求an.

教师要在课题上通过实物投影等方式展示学生收集的成果，并进行系统的指导。如前3个例题是关于前n项和与通项的关系，例题4是数列相邻项的递推关系，这是本节的两类最基本的类型。

三、提高复习效率，选择合适的教辅资料

高三复习资料多如牛毛，足以让教师和学生挑花眼。从实际使用效果看，每种资料都有优劣。选择的关键在于结构是否合理。首先，他会对这一节课有个概述；然后会罗列出重要的知识点；第三，对容易出错误的知识进行解析；第四，列举几个非常经典的题目进行解析，并配有合理的变式训练；第五，题目是否适合学生的学情。而教师手里应该有多种资料，作为复习课备课的重要补充。

四、注重“三化”，当堂过手

“三化”是指基础知识习题化、章节考点网络化、例题习题序列化。

基础知识习题化：数学的基础知识大多枯燥乏味，死记硬背费力不讨好，不如用简单的判断题、选择题、填空题来促使学生动手动口。基础知识用小题的形式呈现，可以让学生学得更加清晰甚至会更加轻松。如等差数列的复习中，可以设计几个判断题来复习基础知识：

（1）若一个数列从第二项起每一项与它的前一项的差都是常数，则这个数列是等差数列。（×）

（2）数列｛an｝为等差数列的充要条件是对任意n∈N*，都有2an+1=an+an+2.（√）

（3）等差数列{an}的单调性是由公差d决定的。（√）

（4）数列｛an｝为等差数列的充要条件是其通项公式为n的一次函数。（×）

（5）数列｛an｝满足an+1-an=n，则数列{an｝是等差数列。（×）

章节考点网络化：指知识考点要连成线，织成网，建立内在的逻辑联系。只有这样，才能更好地形成一个总的知识系统。

例题习题序列化：2～3个典型的、至少一个有教师规范板书的、必须体现得分点的例题；2～3个对应变式练习；6～8个课外练习题，根据版块的要求适当安排解答题的个数。仍以等差数列的复习举例：

题型一　等差数列基本量的运算

例1在数列｛an｝中，若a1=-2，且对任意的n∈N*有2an+1=1+2an，则数列｛an｝前10项的和为（　）(www.daowen.com)

A.2　B.10　C.　D.

变式1若等差数列｛an｝的前5项和S5=25，且a2=3，则a7等于（　）

A.12　B.13　C.14 D.15

题型二　等差数列的性质及应用

例2 （1）设等差数列｛an｝的前n项和为Sn，若S3=9，S6=36，则a7+a8+a9等于（　）

A.63　B.45　C.36　D.27

（2）若一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，则这个数列的项数为（　）

A.13　B.12　C.11　D.10

变式2设数列｛an｝是等差数列，若a3+a4+a5=12，则a1+a2+…+a7等于（　）

A.14　B.21　C.28　D.35

题型三　等差数列的判定与证明

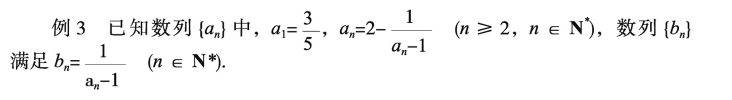
（1）求证：数列｛bn｝是等差数列；

（2）求数列｛an｝中的最大项和最小项，并说明理由。

另外，在例题和对应变式练习中，注意一题多解和多题一解。

五、适时插入“微专题”，以小见大

“微专题”教学是指针对某一具体知识点，从该知识的“三基”入手，整合并运用基本概念和基本原理解决问题的一种“小切口”教学方法。其最大特点集中于一个“微”字，内容适量，着力于某一个具体问题的解决。如在数列的递推关系问题中，选择an与Sn递推关系相关问题作为一个微专题，通过以下几个步骤完成一个专题的复习：

（1）展示高考题目。（2015·全国Ⅱ卷）设Sn是数列｛an}的前n项和，且a1=-1，an+1=SnSn+1，则Sn=________.

（2）明确高考定位。an与Sn递推关系是其中的热点，常在解答题中的第（1）问出现，也时常出现在小题中，难度中档以下。

（3）拿出关键公式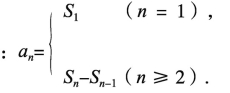

（4）分两类典型例题详细讲解并配以对应变式训练。

一类是消去Sn的：

例1.（2015·全国Ⅰ卷）Sn为数列{an｝的前n项和，已知an＞0，求｛an｝的通项公式；

练习.（2016·全国Ⅲ卷）已知数列｛an｝的前n项和Sn=1+λan，其中λ≠0.

第二类是消去an的：

例2.设数列{an}的前n项和为Sn，已知a1=1，a2=2，且an+2=3Sn-Sn+1+3，n∈N*，证明：an+2=3an；并求an.

在这个过程中，要让学生主动分析问题，解决问题，树立强烈的得分意识。

（5）总结归纳，课后强化。

在高三数学复习中，还要特别重视师生间的沟通和交流，这种交流包括情感的沟通和知识的沟通。有一些学生的数学基础薄弱，教师要抓住机会进行鼓励，多进行基础训练，并找到合适的机会让他们在全班同学面前展示，消除其恐惧心理。在高三的课堂上，要让学生走上讲台，展示自己，提高信心，培养兴趣，还要让学生从“题海战术”中解脱出来。