李　艳

一、一题多变，拓展习题容量（大条件不变，图形相似度高）

例题展示1（七年级下册）

1.如图，D、E分别为等边三角形ABC的边BC、AC上的点，且BD=CE，连接BE、AD，它们交于点F，求证：∠AFE=60°

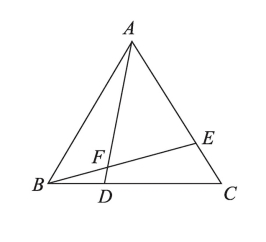
2.△ABC为等边三角形，D、E分别是AC、BC上的点，且AD=CE，AE与BD相交于点P，BF⊥AE于点F，求证：BP=2PF

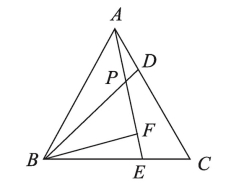
3.在等边三角形ABC中，D、E分别在边BC、AC上，DC=AE，AD、BE交于点F.

（1）请你量一量∠BFD的度数，并证明你的结论；

（2）若D、E分别在边BC、CA的延长线上，其他条件不变，（1）中的结论是否成立？请画图证明你的结论。

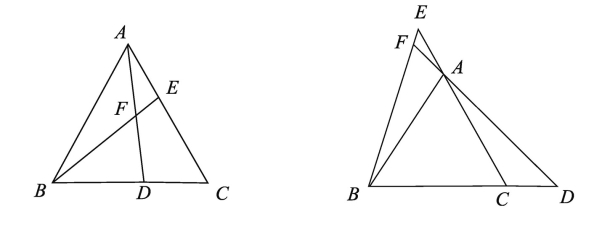
我们看这3个题，大条件都是相同的，1题与2题的大条件相同，2题比1题多了一个条件，问法发生变化，初看很难切入主题解决问题，但是在1题的基础上，我们可以拓展开来，如果对1题的解法很熟悉，2题的解决也就轻松了。再比较1题和3题发现条件相同，但是问问题的方式不同，一个直接提问，一个间接提问，3题在1题的基础上继续拓展了能力，但是思路是一致的（第一步都必须证全等）。这3个题既有联系，又有区别，但是我们会发现图形的相似度高达95%。通过对这3个题的分析和对比学习，我相信学生在后面遇见类似题型（选择、填空、解答都可能），思维就会比较活跃，解题能力能够大大提升。

二、一题多变，解法思路互逆（条件结论互换，图形不变，升华结论）

例题展示2（七年级下册）

1.如图，已知∠B=∠C=90°，M是BC的中点，DM平分∠ADC，求证：

（1）AM平分∠DAB；

（2）DM⊥AM.

（解题方法：延长DM，延长AB交于点N，

第一步证△DCM≌△NBM，第二步证△AMD≌△AMN）(www.daowen.com)

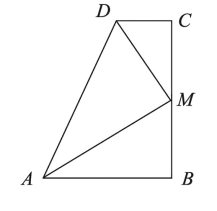
2.如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F，求证：（1）FC=AD；（2）AB=BC+AD.

（解题方法：第一步证△ADE≌△FCE，第二步证△ABE≌△FBE）

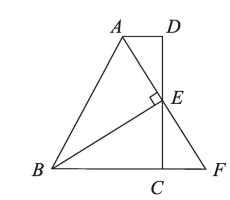
3.已知：如图，CB⊥AB，CE平分∠BCD，DE平分∠CDA，∠1+∠2=90°，求证：DA⊥AB

（解题方法：证∠ADC+∠BCD=180°）

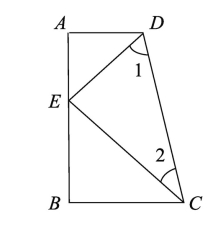
4.如图，AD∥BC，AB=AD+BC，EA、EB分别平分∠DAB、∠CBA，CD过点E，点F在AB上，且AF=AD，若AE=5、BE=4，求四边形ABCD的面积。

（解题方法：连接EF证△ADE≌△AFE，再证△BFE≌△BCE，最后说明∠AEB=90°）

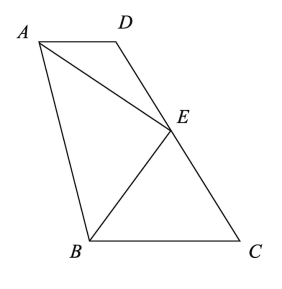
5.两个全等的含30°、60°角的三角板ADE和三角板ABC如图所示放置，E、A、C三点在一条直线上，连接BD，取BD的中点M，连接ME、MC，试判断△EMC的形状，并说明理由。

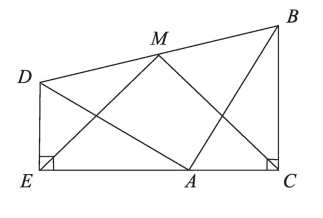
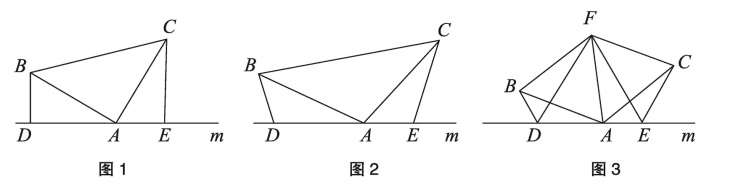
6.（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，证明：DE=BD+CE

（2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角。请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由。

（3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状。

我们来看这6个题，首先看前4个题主体图形基本一致（梯形中的变换），摆放的方位和角度稍有差别。1题和2题都有中点，都有上下平行（1题平行需要证明2题平行直接给出），1题辅助线的添加后即成为2题的图形，证两个三角形全等的条件和结论刚好互换（△ABE≌△FBE和△AMD≌△AMN）。3题条件变换倒过来证上下平行，条件和结论跟1题互换。4题在2题的基础上改变了部分条件，所提问题难度有增加，但是基于2题的基础思路打开了也容易解答。将不规则图形面积问题转化为规则图形和已知条件能解决。最后我们来看5题和6题保有梯形的大体结构特征，但是问题升华，5题保有了梯形中一对边平行，一边上中点的特征，增加了特殊的直角三角形，拓展了知识点的应用。6题继续在5题的基础上加大难度层层递进，从特殊直角三角形变换为一般情况，再次将题的知识范围拓展，应用能力提升。

综合发现：通过做这样的有针对性的对比练习，可让学生掌握类比的数学思想，培养学生寻找共性，克服困难的信心，将知识系统化。当然，数学的学习，除了学习方法的优选，还需要兴趣的培养。在方法与兴趣的双重作用下，才能更好地学好数学。