高兴茹　徐 侃　韩 烁　曾子虹

摘 要：本文主要就ZKY-SS型声速测定实验仪接收换能器声压随位置变化进行了理论模拟研究和实验探讨。 理论模拟结果与文献 ［4］ 给出的结论有较大的分歧。 具体实验测量也与其理论模拟结果并不一致。 另外， 本文研究了在不同媒质中 （清水和模拟海水） 接收换能器声压随位置变化情况， 实验发现接收换能器声压随位置变化是非线性变化的， 且随模拟海水的浓度变化而变化。

关键词： 接收换能器， 超声波， 媒质， 声压

1. 引言

大多数声速测量实验均基于压电陶瓷换能器将机械能转换成电能进行电测的［1-10］，该实验的实验原理非常简单， 即通过改变接收换能器与发射换能器的距离， 测出波长，根据关系式：υ＝f·λ计算出声速［11］。然而，在测量过程中却存在着诸多问题引起了广泛的争议［12-14］。究其原因主要是由于媒质对声波有吸收，同时声波在换能器表面反射时并非全反射导致多次反射波相干叠加致使接收换能器声压随位置变化甚为复杂［15-16］，并非像大多数实验教材所写的为简单的驻波。

为此， 我们对ZKY-SS型声速测定实验仪在不同媒质中接收换能器声压随位置变化进行了实验探讨， 并试图找到其变化规律。 由于接收换能器声压振幅随距离变化的特性比较复杂， 很少有人对声压振幅的规律进行较深入的研究。 文献 ［4］ 在这方面做了一定的尝试， 通过大量的数据计算， 给出了接收换能器的声压振幅A随距离x变化的数学方程。 本文对该方程进行了数值模拟， 模拟结果与文献 ［4］ 有较大出入。

2. 接收换能器声压随位置变化的数学方程及数值模拟

文献 ［4］ 对多种数学模式试探， 并进行了大量的数据计算。 给出了共振干涉法接收换能器的声压振幅A随距离x变化的数学方程为：

其数值模拟曲线如图1所示。 由此可见， 接收换能器声压峰值点间的距离是等间距的， 但峰值并非简单地按指数规律衰减， 这与其实验结果并不一致。 该方程与实际数据出现自相矛盾的情况。 图2为文献 ［4］ 的理论值、 实验值以及我们对该方程的模拟值曲线， 模拟值曲线峰值点按指数衰减， 而文献 ［4］ 的理论值曲线峰值点基本保持不变。

图1

图2

3. 接收换能器声压随位置变化的实验研究

由于模拟值曲线峰值点与文献 ［4］ 的理论值曲线峰值点的变化情况存在较大的差异， 所以我们希望通过了解峰值点的变化情况来进一步探索这种规律。 于是本文开始研究声速测定实验仪在空气中的声压随位置的变化。 在实验测量时发现发射与接收换能器距离较近与较远时情形并不相同。 当两者距离较近时， 主峰的峰值点等间距且幅值基本不变， 次峰峰值点幅值呈衰减趋势， 在发射与接收换能器间距在0～3.86mm内， 声压幅值递减且没有次峰及再次峰出现， 在3.86mm之后声压幅值呈现一定的规律变化。根据对波长的计算λ／2＝4.6092mm可知在发射与接收换能器间距小于半波长时一次及以上反射波并不会出现， 接受换能器接收的仅仅是发射换能器直接发射出的超声波， 随着两者间距离的增大， 由于空气的阻尼， 使得声压幅值减小。 当发射与接收换能器距离较远时， 次峰及再次峰均没有出现， 且声压峰值点随距离的增大缓慢减小， 但却并没有出现指数衰减的趋势。

3.1 发射换能器与接收换能器距离较近时

对实验数据做了上述的模拟（f＝37.565kHz），从图3中发现了5个次峰可能存在的位置， 对此我们在这5个位置周围做了更加精细的测量， 证明了这5个次峰的存在。根据公式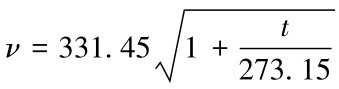（t＝25℃）计算可得ν＝346.29m／s。近而可以计算求得波长λ＝9.2184mm。从图3中可得出5个次峰的峰值点，其位置如表1所示。

图3

表1 次峰位置 （实验测量值） mm

文献［5］指出在间距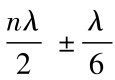处会产生次峰，其值如表2所示。

表2 次峰位置 （文献 ［5］ ） mm

根据实验数据图3可知在x1＝5.78mm，x2＝10.46mm，x3＝15.06mm，x4＝19.74 mm，x5＝24.36mm处出现主峰。相邻的主峰与次峰的间距为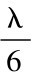［5］（1.5364 mm）。

根据表1测量数据求得两者间距分别为x1＝1.34mm，x2＝0.64mm，x3＝1.04 mm，x4＝1.26mm，x5＝1.58mm。这与文献［5］ 的结论存在较大的差异。

次峰及再次峰将会服从一定规律不间断出现［5］。但根据文献［5］ 的数据测量见图4， 以及实验测量数据见图3和图5， 次峰仅仅只是在发射与接收换能器距离较近时才出现。 并且当发射与接收换能器距离较近时， 接收器表面声压随距离的增大并没有按指数衰减的趋势， 这与文献 ［5］ 的实验数据曲线并不相符。 对于次峰及再次峰的出现情况，由于空气的阻尼不能忽略，并且在发射与接收换能器表面的发射并非全反射［3］导致每次反射声波均有损耗。 当发射与接收换能器距离较远时， 再次峰需要声波的反射次数更多， 以及声波走过的距离相比与次峰更长， 所以再次峰的出现相比与次峰更为困难， 所以只要次峰不出现在主峰的周围， 再次峰一定不会出现。

图4

3.2 发射换能器与接收换能器距离较远

当发射与接收换能器距离较远时， 实验过程中没有次峰出现， 与文献 ［4］ 给出的结论 （见图1） 完全不同。 实验发现声压峰点、 谷点的幅值随发射与接收换能器距离缓慢变化， 实验数据曲线如图5所示。 随着发射与接收换能器距离增大的过程中， 在75～165mm区间内， 波腹的声压幅值基本保持不变， 而谷点的声压幅值却随距离的增加而逐渐增加； 而在距离超过165mm后谷点的声压幅值却基本保持不变， 峰点的声压幅值却随距离的增加而逐渐减小。

图5

4. 不同介质中接收换能器声压随位置变化

由于峰值点变化情况的复杂， 为了更加清晰地看出峰值点变化的规律， 于是我们在测量时只记下峰值点所在的位置（见图6）。但在145mm左右处出现的峰值点急剧减小，所以我们增加了测量点数从而一定程度上了解声压峰值点在此处的衰减情况。 从图6中可以看出在0～130mm声压峰值点的变化幅度比较小， 在145mm处峰值点发生突变。

图6

4.1 清水中

4.2 浓度为9％的模拟海水

由于在清水中发现了这种峰值点突变的关系， 在改变其浓度后这种现象还会有吗？于是我们测量了在浓度为9％的模拟海水中声压峰值点所在的位置并绘制成如图7所示的曲线。 声压峰值点的突变情况依旧存在， 只是突变幅度相较与清水更加缓和。(www.daowen.com)

图7

4.3 不同浓度的海水

在不同媒质中 （清水和模拟海水） 接收换能器声压随位置变化情况是完全不同的，由此可见， 当模拟海水的浓度 （含盐百分比） 变化时， 文献 ［16］ 研究了声速随模拟海水浓度变化的情况， 其结果是二者间存在线性变化关系。

从图8中可以看出， 声压幅值并没有随模拟海水浓度的增加而呈现近似线性增加的趋势， 这与文献 ［16］ 的测量结果有较大的出入。

图8

于是我们想在改变了模拟海水的浓度后， 相同的位置上的声压幅值会有什么样的关系？ 实验数据 （见图8）， 在模拟海水浓度在0～1.8％范围内声压值呈线性关系分布（见图9）。 但其他区域上并没有这种关系。 根据这种线性关系， 通过声呐技术测量海水盐度变为可能。 希望后续的研究人员能继续研究， 为测量海水盐度提供了一种新方法。

图9

在发现这种线形关系后， 我们增加了测量组数发现在模拟海水浓度在0～1.0％浓度内， 发射与接收换能器间距距离20cm和24cm两条曲线变化幅度较大。 在模拟海水浓度在1.0％～4.0％内，7条曲线均十分稳定。 但在模拟海水浓度为4.0％～7.0％内， 16 cm的曲线波动幅度较大 （见图10）。

图10

5. 结论

本文用文献 ［4］ 的数学方程所得的模拟曲线峰值点与文献 ［4］ 的理论峰值点存在较大的出入， 经本文实验探究声压峰值点并不是按照指数递减的。 希望后续的研究人员能更加进一步推导出声压幅值随距离变化的函数关系。

文献 ［4］ 的模拟值、 理论值与测量值均没有出现次峰及再次峰， 但在发射与接收换能器距离较近时， 本文实验得出的图3有次峰的存在。 使得在发射与接收换能器距离较近时的次峰存在与否与文献 ［4］ 存在一定的出入。

从图8中可以看出， 声压幅值并没有随模拟海水浓度的增加而呈现近似线性增加的趋势， 这与文献 ［16］ 的测量结果有较大的出入。 但在一个小区间内， 声压幅值随模拟海水浓度的增加而线性减小， 这使得通过声呐技术测量海水盐浓度变为可能。

参考文献

［1］ 高兴茹， 倪苏敏， 张义民. 大学物理实验讲义 ［M］. 北京： 中国科学技术出版社，2004：118-124.

［2］ 江兴方.声速测量实验中的三点思考［J］.大学物理，2002，22（3）：28-30.

［3］ 刘香茹， 曹万民， 巩晓阳. 声速测量原理中的两个问题 ［J］. 洛阳工学院学报，2001，22 （3）：86-88.

［4］ 许定生， 周炎辉， 白志刚， 夏樟根， 娄彝忠. 声速测量实验中压电接收端的声压随位置变化的规律［J］. 物理与工程，2002，12 （2）：35-36，44.

［5］ 张宝峰， 刘裕光， 张涛华. 声速测量实验中界面反射问题的探讨 ［J］. 物理实验，2001 （8）：10-12.

［6］ 傅光华， 吕涛.SYY型声速测量仪及其使用 ［J］. 教学仪器与实验， 1991 （3）：10-14.

［7］ 黄贤群.SW-1型声速测定仪的改进及声速测量方法的研究 ［J］. 韩山师范学院学报，2008，29 （6）：49-52.

［8］ 魏国瑞， 潘沛， 张建国， 李隆. 超声波测量新方法 ［J］. 西安建筑科技大学学报（自然科学版），2004，36 （3）：375-378.

［9］ 王山林. 关于声速测量实验的研究与设计 ［J］. 廊坊师范学院学报 （自然科学版），2012，12 （1）：45-46.

［10］ 于连生. 毫米级高精度海水声速测量技术研究 ［J］. 海洋技术， 2003， 22 （3）：63-64，73.

［11］ 陈金坤. 声速测量实验仪器和方法的改进 ［J］. 福建师范大学福清分校学报，2002 （2）：64-66.

［12］ 程晶晶， 孔力， 黄臻. 一种改进的超声波液位测量声速的校正方法 ［J］. 武汉理工大学学报（信息与管理工程版），2007，29 （2）：40-43.

［13］ 刘镇清. 一种改进的脉冲回波声速测量方法 ［J］. 实验技术与管理， 1992， 9 （2）：29-32.

［14］ 孔正坤. 一种声速测量实验仪器的研究 ［J］. 云南师范大学学报， 1996， 16 （3）：52-55.

［15］ 谢宜臣. 自制声速测量装置 ［J］. 教学仪器与实验， 1985， 1 （4）： 27-28，30.

［16］ 邢键，孙晶华. 水中声速的测量［J］. 物理实验，2011，31 （1）：34-35.