第三节　动态评价方法

考虑资金时间价值的评价方法叫动态评价方法。它以等值计算公式为基础，把投资方案中发生在不同时间点的现金流转换成同一时点的值或者等值序列，计算出方案的特征值（指标值），然后依据所选定的指标基准值并在满足时间可比的条件下，进行评价比较，以确定较优方案。

动态评价方法主要包括净现值法、净现值比率法、净年值法、费用现值法、费用年值法、内部收益率法、动态投资回收期法等。

一、净现值法

1．定义

净现值指标要求考虑项目寿命期内每年发生的现金流量，净现值是指按一定的折现率（或基准折现率），将投资方案在寿命期内各年净现金流量折现到同一时点（通常是期初）的现值代数和就是净现值。

2．计算公式

净现值的计算公式为：

式中：NPV为净现值；（1＋i₀）^－t为第t年的折现系数（或贴现系数）；i₀为基准折现率；n为投资方案的寿命期。

若工程项目只有初始投资，以后各年末的净收益相等，则NPV计算可表示为：

NPV＝－I＋A（P／A，i，n）　　　　　　　（4－8）

3．判别标准

若NPV≥0，可以考虑采纳该投资项目；若NPV＜0，应该舍弃该投资项目。

多方案比选时，应选择净现值最大的方案，净现值越大的方案相对越优（净现值最大准则）。

【例4－3】　在例4－2中，试计算折现率为10%时的净现值，并判断项目是否可行。

【解】　根据题意画出现金流量图如图4－1所示。

图4－1　斯库尔油田天然气开采项目净现金流量图

解法一：NPV＝－500－200（1＋10%）^－1－600（1＋10%）^－2－600（1＋10%）^－3－200（1＋10%）^－4＋700（1＋10%）^－5＋1200（1＋10%）^－6＋1200（1＋10%）^－7＋1200（1＋10%）^－8＋600（1＋10%）^－9＋600（1＋10%）^－10＋600（1＋10%）^－11＋600（1＋10%）^－12＋600（1＋10%）^－13

　　　　　＝1583．68（万元）

解法二：NPV＝－500－200（P／F，10%，1）－600（P／A，10%，2）（P／F，10%，1）－200（P／F，10%，4）＋700（P／F，10%，5）＋1200（P／A，10%，3）（P／F，10%，5）＋600（P／A，10%，5）（P／F，10%，8）

　　　　　＝1583．54（万元）

解法三：净现值也可采用现金流量表来计算，如表4－2所示。

表4－2　斯库尔油田天然气开采项目净现金流量过程贴现值表　　　　　　　　　单位：万元

4．净现值函数

从净现值计算公式（4－7）可以看出，若不改变净现金流量而变动折现率i，NPV将随i的增大而减小。当i连续变化时，可以得到NPV与i变化的函数，即净现值函数。现举例分析。

【例4－5】　某石油工程项目初始投资500万元，寿命期10年。在10年内每年净收益均为140万元，试画出净现值函数曲线。

【解】　NPV随折现率i变化的数值如表4－3所示。

表4－3　不同的i所对应的NPV值

由表4－3可知，NPV将随i的增大而减小，现画出净现值函数曲线，如图4－2所示。

图4－2　净现值函数曲线

从图4－3中，可以发现净现值函数的特点。

（1）同一净现金流量其净现值随折现率（i）的增大而逐渐减小。故当基准折现率（i₀）越大，则净现值就会越小，甚至为零或负值，因而可能被接受的方案就越少。

（2）净现值随折现率的增大可从正值变为负值，因此，必然有当i为某一数值i＊时，使得净现值NPV＝0，如图4－2所示，i（%）＜i^＊时，NPV_（i）＞0；i＞i^＊时，NPV_（i）＜0；只有当净现值函数曲线与横坐标相交时（即i^＊＝25%，NPV_（i）＝0），i^＊是一个具有重要经济意义的折现率临界值，后面还要对它作详细分析。

5．净现值对i的敏感性问题

净现值对折现率（i）的敏感性问题是指，当i从某一值变为另一值时，若按净现值最大的原则优选项目方案，可能出现前后相悖的情况。表4－4中列出了两个互相排斥的方案A和方案B的净现金流量及其所在折现率分别为10%和20%时的净现值。

表4－4　方案A、B在基准折现率变动时的净现值　　　　　单位：万元

由表4－4可知，在i为10%和20%时，两方案的净现值均大于零。根据净现值越大越好的原则，当i＝10%时，NPV_A＞NPV_B，故方案A优于方案B；当i＝20%时，NPV_A＜NPV_B，则方案B优于方案A，这一现象对投资决策具有重要意义。例如，假设在一定的基准折现率（i₀）和投资总限额I₀下净现值大于零的项目有5个，其投资总额恰为I₀，故上述项目均被接受；按净现值的大小，设其排序为A、B、C、D、E。但当投资总额压缩至I₁时，新选项目是否仍然会遵循A、B、C、D、E的原来顺序直至达到投资总额为止呢？一般来说不会的。随着投资额的减少，为了减少被选取的方案数（准确地说，是减少被选取项目的总投资额），应当提高基准折现率，但基准折现率提高到一定数值时，由于各项目方案净现值对基准折现率的敏感性不同，原先净现值小的项目，其净现值现在可能大于原先净现值大的项目，因此，在基准折现率随着投资总额变动的情况下，按净现值准则选项目不一定会遵循原有的项目排列顺序。所以，基准折现率是投资项目经济效果评价中一个十分重要的参数。

6．对NPV指标的评价

NPV指标的优点：考虑了资金的时间价值，可以清楚地表明方案在整个寿命期内的绝对收益，简单、直观。

NPV指标的局限性：折现率或基准折现率的确定比较困难，但折现率或基准折现率的大小又直接影响方案的经济性。若折现率或基准折现率选取得过高，则会使经济效果较好的方案变为不可行；选取得太低，又会使经济效果不好的方案变为可行。此外，净现值所反映的是方案绝对经济效益，不能说明资金的利用效果大小。当各方案投资不同时，易选择投资大、盈利也大的方案，而忽视投资较少、盈利较多的方案。特别是当各方案投资额相差很大时，仅根据净现值的大小选取方案可能会导致错误的选择。为了解决这一问题，常需要借助于净现值比率这一指标。

二、净现值比率法

净现值比率法（又称净现值指数法）是在净现值法的基础上发展起来的。当净现值用于多方案比较时，虽然能反映每个方案的盈利水平，但是由于没有考虑各方案投资额的多少，因而不能直接反映资金的利用效率。为了考察资金的利用效率，可采用净现值比率作为净现值的一个补充指标。

1．定义

净现值比率是方案的净现值与投资现值之比，它反映了单位投资现值所获得的净现值。也就是单位投资现值所取得的超额净收益，净现值比率的最大化将有利于实现有限投资取得净贡献的最大化。

2．计算公式

净现值比率计算公式为：

式中：NPVR为净现值比率；I_t为第t年的投资；I_p为投资现值，即如果工程项目的投资是分次投入，应将各次投资均换算为现值后相加。

3．判别标准

净现值比率反映了方案的相对经济效益，净现值比率越大，投资方案的经济效益越好。

当NPVR≥0时，方案可行，可以考虑接受；当NPVR＜0时，方案不可行，应予以拒绝。

用净现值比率进行方案比较时，应选择净现值比率最大的方案为优，净现值比率一般作为净现值的辅助指标来使用。净现值比率主要适用于多方案的优劣排序。

净现值指标与净现值比率指标两者关系密切。一般情况下，净现值大的方案，其净现值比率也大，但有时净现值最大的方案，其净现值比率并不大。当用净现值与净现值比率两个指标在选择方案发生矛盾时，应区别不同情况，作出恰当的选择。在资金供应充足即无资金限额时，我们可以追求最大收益，而不太注重资金的利用效果是否最大。此时应以净现值作为评价标准，选择净现值最大方案为最优方案。在资金供应紧张或各方案投资额相差很大时，我们强调资金的利用效果，即单位投资应获得较高的收益。此时应以净现值比率为评价标准，选择净现值比率最大的方案为最优方案。

【例4－4】　油田采油有A、B两个方案均可行，现金流量如表4－5所示。基准收益率为10%，试用净现值法和净现值比率法比较评价选优。

表4－5　A、B方案现金流量表　　　　　　　　单位：万元

【解】　按净现值评价优选

由于NPV_B＞NPV_A，所以方案B为优选方案。

按净现值比率评价优选：

由于NPVR_A＞NPVR_B，所以方案A为优选方案，这与用净现值法计算的结论相反。

由此可见，当方案的投资额不相等时，除用净现值法外，往往需要用净现值比率作为辅助评价指标，才能作出合理的评价。

本例中，方案A的净现值率为0．7135，其经济含义是方案A除了有10%的基准收益率外，每万元现值投资尚可获得0．7135万元的现值收益。

4．对NPVR指标的评价

NPVR指标的优点：净现值比率指标能明确反映单位投资可获得的净现值。这对于提高资金利用效果，加强资金运用的管理工作有着重大的意义。该指标与净现值指标紧密结合，既考虑了投资方案的绝对值收益，又考虑了其相对经济效益。

NPVR指标的局限性：在多方案选择时，易选择投资较少、收益较大的方案，而放弃投资大、收益也大的方案。

三、净年值法

净年值法是年等值法的一种。其基本思路是不论方案在寿命期最小公倍数的时间内重复多少次，其年值是等值的。所以，只要计算各方案在各自寿命期的净年值就可以进行方案的比较。

1．定义

净年值就是以基准收益率或给定的折现率将投资方案寿命期内的各年净现金流量均换算为等额年值。

2．计算公式

净年值计算公式为：

式中：NAV为净年值；（A／P，i，n）为等额支付系列资金回收系数，其余符号意义同式（4－7）。

若投资方案只有一次初始投资I，以后各年有相同的净收益A，且寿命期末残值为S。则净年值可表示为：

NAV＝A－I（A／P，i，n）＋S（A／F，i，n）　　　　　　　　（4－11）

4．判别标准

当NAV≥0时，方案可行，则项目在经济效果上可以考虑接受；当NAV＜0时，方案不可行，则项目在经济效果上应予以拒绝。

多方案比较时，应选择NAV＞0，且NAV最大的方案为最优方案。

将净现值的计算公式及判别标准与净年值的作比较可知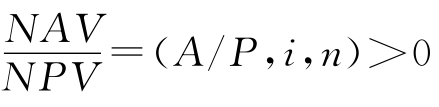，，故净年值与净现值在项目评价的结论上总是一致的。因此，就项目的评价结论而言，净年值与净现值是等效评价指标。净现值给出的信息是项目在整个寿命期内获取的超出最低期望盈利的超额收益的现值，与净现值所不同的是，净年值给出的信息是寿命期内每年的等额超额收益。由于信息的含义不同，而且由于在某些决策结构形势下，采用净年值比采用净现值更为简便和易于计算（后面再详述）。

四、费用现值与费用年值

在对多个方案比较选优时，如果诸方案产出价值相同时，或者诸方案能够满足同样需要但其产出效益难以用价值形态（货币）计量（如环保、教育、保健、国防等）时，可以通过对各方案费用现值或费用年值的比较进行选择。

（一）费用现值

1．定义

费用现值法就是将工程服务年限内的年经营费用以基准贴现率或给定的折现率折现为现值与项目的投资现值相加（若有残值应扣除残值的现值），以求得工程项目总费用现值。

2．计算公式(www.daowen.com)

费用现值计算公式为：

式中：PC为费用现值；C为年的经营成本；S为计算期末回收的固定资产余值；W为计算期末回收的流动资金。

（二）费用年值法

1．定义

费用年值法是指以基准折现率或给定的折现率，把各个方案的费用转化为经济寿命期内的等额年值，或者直接将费用现值换算为等额年值。

2．计算公式

费用年值计算公式为：

费用现值与费用年值指标只能用于多个方案的比选，其判别标准是：费用现值或费用年值最小的方案为最优方案。

五、内部收益率法

内部收益率法和净现值法一样，是石油技术经济评价指标中最重要的评价指标之一。

1．定义

所谓内部收益率，就是使净现值为零时的折现率。内部收益率是效率型指标，它能够反映项目所占用资金的盈利率，即考察项目资金使用效率的重要指标。

在图4－2中，随着折现率的不断增大，净现值则不断减小。当折现率增至25%时，此时项目净现值为零。对该项目而言，其内部收益率即为25%。一般而言，NPV与横坐标交点处对应的折现率就是内部收益率。

2．计算公式

内部收益率可从式（4－14）的计算得出：

式中：IRR为内部收益率。

若投资方案只有一次初始投资I，以后各年有相同的净收益A，则内部收益可表示为：

－I＋A（P／A，IRR，n）＝0　　　　　　　　　（4－15）

3．计算方法

由式（4－14）知，当t＝0，1，2，…，n时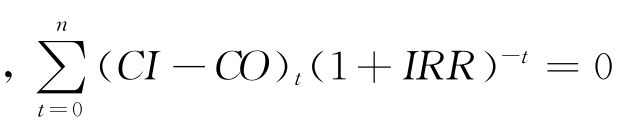是一个高次方程，不能采用一般的代数方法求解，通常采用“试算内插法”求IRR的近似解，求解过程如下：

先任意取一个折现率i₁，计算相应的NPV（i1），若NPV（i1）＞0，说明欲求的IRR＞i₁，则增加折现率i₁的值，若NPV_（i1）＜0，说明欲求的IRR＜i₁，则减小折现率i₁的值，根据此信息，将折现率修正为i₂，求NPV_（i2）的值。如此反复试算，直到净现值等于零或接近于零为止，然后用线性插值的方法求出内部收效率IRR的近似值。计算公式为：

图4－3　用内插法求IRR图解

式中：i₁、i₂分别是使净现值由正转为负的两个相近折现率，且i₂＞i₁；NPV_（i1）、NPV_（i2）分别为i₁、i₂时计算的净现值，NPV_（i1）＞0，NPV_（i2）＜0。

式（4－16）的推导可参照图4－3，该图根据净现值与折现率的函数关系画出。当i₁与i₂很接近时，可将曲线段︵AB近似看成直线段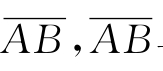

与横坐标交点处的折现率i＊即为IRR的近似值，三角形△Ai₁i^＊相似于△Bi₂i^＊，根据相似三角形原理可得：

由于上式计算误差与i₂－i₁的大小有关，且i₂与i₁相差越大，误差也越大，为控制误差，i₂与i₁之差一般不应超过5%。

5．判别标准

计算出内部收益率IRR后，应与基准收益率i₀相比较。

若IRR≥i₀，则认为方案在经济效果上是可行的，可以考虑采纳该投资项目；若IRR＜i₀，则认为方案在经济效果上是不可行的，应放弃该投资项目。

在多方案比选中，若各方案内部收益率IRR₁，IRR₂，…，IRR_n，均大于i₀，均可取，则此时应该与净现值指标结合起来考虑。一般是选择IRR较大且NPV也较大的方案，而非IRR越大的方案就越好。

【例4－5】　在例4－2中，设其行业基准折现率为15%。试用内部收益率法分析判断方案是否可行。

【解】　根据式（4－14）得：

－500－200（P／F，IRR，1）－600（P／A，IRR，2）（P／F，IRR，1）－

200（P／F，IRR，4）＋700（P／F，IRR，5）＋1200（P／A，IRR，3）（P／F，IRR，5）＋600（P／A，IRR，5）（P／F，IRR，8）＝0

设i₁＝22%，i₂＝23%，分别计算其净现值。

NPV₁＝－500－200（P／F，22%，1）－600（P／A，22%，2）（P／F，22%，1）－200（P／F，22%，4）＋700（P／F，22%，5）＋1200（P／A，22%，3）（P／F，22%，5）＋600（P／A，22%，5）（P／F，22%，8）

　　　　　　　　＝28．16（万元）

NPV2＝－500－200（P／F，23%，1）－600（P／A，23%，2）（P／F，23%，1）＋200（P／F，23%，4）＋700（P／F，23%，5）＋1200（P／A，23%，3）（P／F，23%，5）＋600（P／A，23%，5）（P／F，23%，8）

　　　　　　　　＝－43．81（万元）

再用内插法计算出内部收益率IRR：

由于IRR（22．39%）大于基准折现率（15%），故斯库尔油田天然气开采项目在经济效果上是可以接受的。

6．内部收益率的经济涵义

从内部收益率（IRR）的定义可知，内部收益率是现金流入量的现值与现金流出量的现值相等时的利率，内部收益率完全由方案本身的参数确定，不同方案由于寿命期不等，现金流量模式不同就具有不同的内部收益率。但从内部收益率的经济含义来理解，内部收益率可以有以下几种意义：

（1）如果方案的投资全部靠借款，而还本付息的资金又都来自方案寿命期内现金流入，则内部收益率（IRR）表示方案可以承担的最大贷款利率。表现利率的一个临界值，我们要求贷款利率只能小于它，绝不能大于它。

（2）在方案整个寿命期内，在i₀的条件下，始终存在着未被回收的投资及其利息，仅在方案寿命期末，它们才恰恰被完全回收。所以内部收益率是使现金流入量到方案寿命终了时将投资及其利息抵消为“0”的投资收益率。

【例4－6】　按例4－5的净现金流量及计算求得的内部收益率IRR＝23．31%，计算和分析收回全部投资的过程，如表4－6所示。

表4－6　以IRR为利率的斯库尔油田天然气开采项目投资回收过程计算表　　　　　　单位：万元

由表4－6可以明显看出，从第0年年末直到第13年年末的整个寿命期内，每年均有尚未收回的投资，只有到了第13年年末即寿命期结束时，才完全收回了投资。

为了更清楚、直观地考察和了解内部收益率的经济涵义，将表4－6收回全部投资过程的现金流量变化状况表示为如图4－4所示。

图4－4　以利率i＝IRR收回全部投资过程的现金流量图

由表4－6及图4－4可见，不能将内部收益率错误地理解为一个期初投资的收益率，因为它不仅仅回收期初投资，而是随着时间变化使未回收投资余额得到不断回收的一个利率，只有用这个利率回收投资，在项目寿命期末时投资余额恰好为零。

（3）作为方案的收益率，当方案的收益率小于IRR时，NPV为正值；当方案的收益率大于IRR时，NPV为负值，此时方案不可取（没有经济价值）。而在收益率等于IRR时，NPV正好等于零。所以，内部收益率可以理解为一个临界值，即在方案具有经济价值的前提下，内部收益率可显示方案可以达到的最大可能的收益率。

7．对IRR指标的评价

IRR指标的优点：该指标考虑了资金的时间价值及方案在整个寿命期内的经营情况。此外，还有一个独特的优点是不需要事先设定折现率而可以直接求出。该指标以百分数表示，比净现值更能反映方案的相对经济效益。

IRR指标的局限性：对于非常规投资项目内部收益率可能多解或无解，在这种情况下内部收益率难以确定。

六、动态投资回收期法

投资回收期是分析工程项目投资回收快慢的一种重要方法。作为投资者，非常关心投资回收期。通常，投资回收期越短投资风险就越小。投资回收快，收回投资后还可以进行新的投资。因此，投资回收期是投资决策的重要依据之一。为了弥补静态投资回收期没有考虑资金时间价值的缺陷，现引入动态投资回收期的概念。

1．定义

动态投资回收期就是在基准收益率或一定折现率下，投资项目用其投资后的净收益现值回收全部投资现值所需的时间，一般以“年”为单位。

2．计算公式

动态投资回收期一般从投资开始年算起，由式（4－17）求得：

式中：P′_t为动态投资回收期。

动态投资回收期（P′_t）也可以用项目财务现金流量表中的累计净现金流量计算求得，其计算公式为：

3．判别标准

采用动态投资回收期法进行方案评价时，应将计算所得投资回收期（P′_t）与国家有关部门规定的基准投资回收期（P_t0）相比较，以确定方案的取舍。故其判别标准是：若P′_t≤P_t0项目可以被接受，否则应予以拒绝。

【例4－7】　斯库尔油田天然气开采项目有关数据如表4－6所示。收益率i＝10%，基准动态投资回收期P_t0＝8年，试计算动态投资回收期，并判别该项目是否可行。

表4－6　斯库尔油田天然气开采项目现金流量表　　　　单位：万元

【解】　据式（4－18），求得动态投资回收期，将表4－6中最末一列的有关数据代入式（4－18），得：

因为P′_t＜P_t0，故该项目可行可以接收。

4．对P′_t指标的评价

动态投资回收期指标的优点是概念明确，计算简单，突出了资金回收速度。需要注意的是动态投资回收期与静态投资回收期相比，尽管考虑了资金的时间价值，但仍未考虑投资回收以后的现金流量，没有考虑投资项目的使用年限及项目的期末残值。此外，由于人们对投资与净收益的理解不同往往会影响该指标的可比性。因此，它常常被广泛地用作辅助指标。只有在资金特别紧缺、投资风险很大的情况下，才把动态投资回收期作为评价方案最主要的依据之一。

七、评价指标小结

从经济效果角度评价项目的常用指标，包括净现值、净年值、费用现值、费用年值、净现值比率、内部收益率、投资收益率、静态投资回收期和动态投资回收期。在这些指标中，净现值、内部收益率和投资回收期是最常用的项目评价指标。

就指标类型而言，净现值、净年值、费用现值和费用年值是以货币表述的价值型指标；内部收益率、投资收益率和净现值比率则是反映投资效果的效率型指标。

在价值型指标中，就考察的内容而言，费用现值和费用年值分别是净现值和净年值的特例，即在方案比选时，前两者只是考察项目方案的费用支出。就评价结论而言，净现值与净年值是等效评价指标；费用现值与费用年值是等效指标。图4－5给出了各评价指标的类型及关系。

图4－5　评价指标的类型和关系图

一些主要指标在投资项目评价中的意义也可以由图4－6形象地表示出来。

图4－6　累计净现金流量和累计折现值曲线图

图4－6是根据斯库尔油田天然气开采项目表4－1、表4－2和表4－6的有关数据绘出的示意图。图中项目寿命期为13年，第5年末投资结束并开始投资回收过程，投资总额为BD。在不考虑资金时间价值的情况下，累计净现金流量曲线ADCG在C点与横坐标轴相交，AB表示项目建设期阶段，BH表示生产经营期阶段。静态投资回收期为AC，到项目寿命期末累计净现金流量为GH。

当项目各年净现金流量以基准折现率i₀折现时，累计折现值曲线AD′EF与横坐标轴交于E点，这条曲线反映了项目逐年累计折现值随时间的变化。BD′表示总投资现值，动态投资回收期为AE，项目寿命期末的累计折现值FH即为项目的净现值。

当项目各年净现金流以内部收益率（IRR）折现时，在项目寿命期内累计折现值始终为负值，意味着始终存在未被收回的投资，到项目寿命期结束时，投资恰被全部收回，这意味着若以内部收益率为折现率，项目净现值等于零。