许多年以前，环保主义者注意到每隔4年，旅鼠的种群数量似乎急剧减少。一种通行的推测认为这些极地啮齿动物每隔几季便会前往一处陡峭的悬崖，一头扎下，粉身碎骨。1958年，迪斯尼公司的自然史部门将这一集体自杀场景收录在其获奖影片《白色旷野》中。这些镜头看上去如此令人信服，以至于“旅鼠”一词逐渐被人们用来形容那些盲目跟随大众脚步而走向潜在灾祸的人。这些动物的行为甚至还催生出了一款电子游戏，在游戏中，玩家要阻止这些旅鼠走上迈向死亡的愚蠢征程。

20世纪80年代有人透露，《白色旷野》的摄影组伪造了整个场景。加拿大的一部电视纪录片称，这些旅鼠是专为拍片而购买来的，在拍摄过程中，它们拒不从悬崖上跳下，摄影组便“鼓励”它们越过峭壁边缘。那么，如果集体自杀的猜测并非事实，那么，造成这一种群数量每4年发生一次急剧下降的原因又何在呢？

图　5-8

答案依然隐藏在数学之中。一个简单公式就可以告诉我们这一季度的种群数量和下一季度的种群数量有何不同。首先，假定由于食物供给和天敌等生态因素的作用，旅鼠的数量存在一个上限。设此上限为N 。再设L 为经过上一季并存活下来的旅鼠数量，再加上新一季出生的旅鼠，种群数量上升至K 。而在所有K 只旅鼠中，一部分将不会存活下去。其死亡率为L/N，即前一季的旅鼠数量除以旅鼠数量的上限。于是，共有KL/N 只旅鼠会死亡，而在本季末尾剩下的旅鼠数量则为：

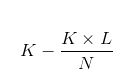
为计算方便，在此设旅鼠种群上限N =100。

该公式尽管简单，却带来一些令人吃惊的结果。首先，如果在每个春天旅鼠的种群数量都加倍，会发生什么情况呢？也就是说K =2 L。其中的2 L× L /100只旅鼠会死掉。假设第1季共有30只旅鼠，根据公式，在第2季的末尾，将会有60-(60×30/100)=42只旅鼠。这一数量会持续增加，一直到第4季，此时将会有50只旅鼠。

而此后，每一季存活下来的旅鼠数量则会一直维持为50只。让人吃惊的是，不管第一季开始时的原始种群数量为多少，最终，在每一季结束后剩下的旅鼠数量总是种群上限的一半。因此，当数量达到50，下一季便会加倍至100只，但到了该季末，其中的100×50/100=50只又会死掉，剩下的旅鼠数量便再次变为50只（见图5-9）。

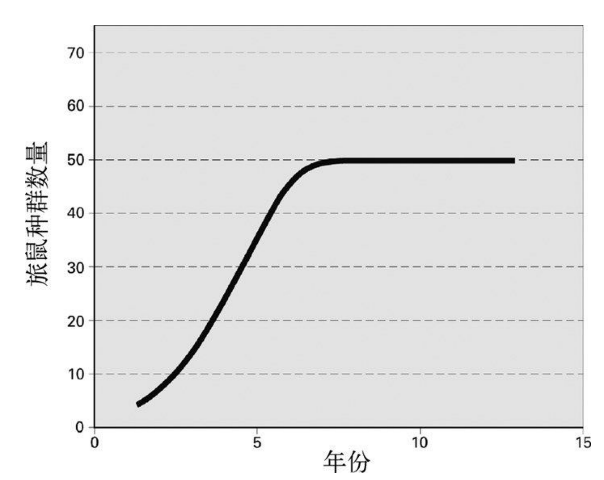
图 5-9　如果旅鼠的种群数量在每个春季倍增，那么不管最初有多少只旅鼠，最终的种群数量都会达到一个稳定值

那么，如果旅鼠的繁殖能力更强又会如何呢？假设，旅鼠种群数量从一季到下一季的时候变为之前的3倍多一点，此时的种群数量并不会抵达一个稳定态，而会在两个数值之间震荡往复。如果某一季存活下来的数量较多，那么下一季存活下来的数量就会变少。

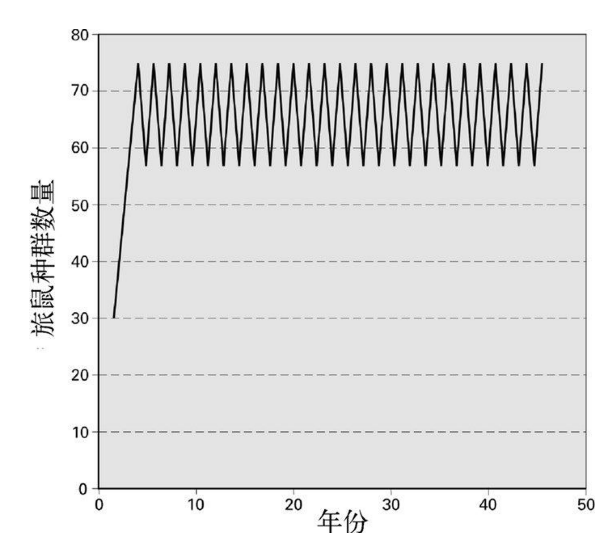
图 5-10　如果旅鼠的种群数量会在春天翻为3倍，以上数值便会发生震荡

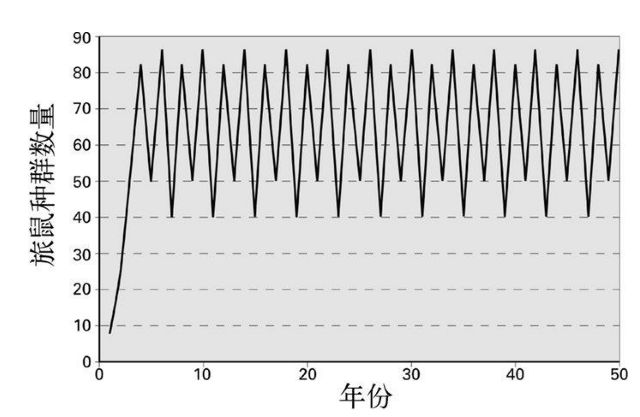
图 5-11　当旅鼠的种群增长因子为3.5时，其种群数量便会在四个不同数字之间震荡往复

当旅鼠的繁殖能力进一步增强后，其种群数量便会以一种更加怪异的方式波动。假如种群数量的增长因子为3.5，那么旅鼠的总数量将在4个数值之间来回振动，每4季重复一次。（而4个数值震荡的情况最早出现在增长因子为1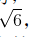+，即大约为3.449的时候。）这种情况便对应了人们发现的每4年一次的旅鼠种群数量急剧下降这一现象。现在我们已经知道了，上述现象的产生并非因为大规模的自杀行为，而是因为数学。

旅鼠种群动态更加有趣的变化则发生在将增长因子提升至3.5699时。此时，种群数量从一季到下一季的震荡似乎变得毫无节奏，毫无缘由。尽管计算这些数量的数学公式依然十分简单，但它已经开始产生混沌的结果。如果改变旅鼠的最初数量，其种群动态则会变得截然不同。只要越过3.5699的门槛，混沌就悄然而至。此时，要预测种群的变化状态就成为几乎不可能完成的任务。掌控种群数量的公式一开始或许可以预期，但只要对旅鼠的繁殖能力做一丁点儿的改动，混沌便即刻凸显出来。

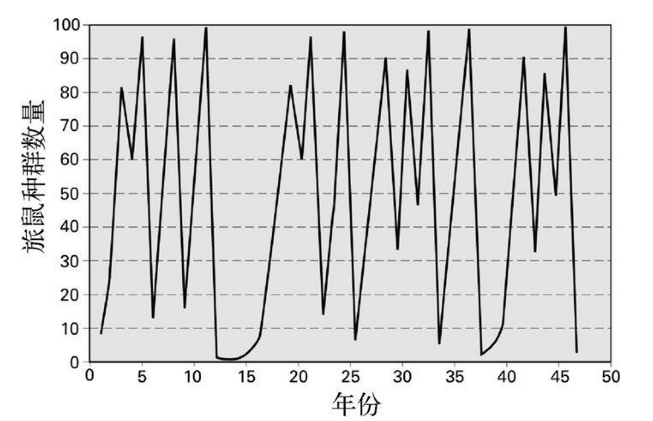
图 5-12　当旅鼠数量在春季的增长倍数达到3.5699或者更高时，其变化曲线将呈现出混沌状态

鱼公式游戏的玩法

这是一个双人游戏，请从本书网站下载相关PDF文件，然后裁切出10只鱼和1个鱼缸。该游戏探索的是鱼群数量在10个季度内的变

化情况。每1条鱼对应1季，在鱼的一侧有1个方格，你可以在此记录下当季鱼缸中鱼的数量。鱼缸中最多可容纳12条鱼。鱼的寿命为1年，在这一年中，它们会产下一定数量的后代，然后死掉。

首先，掷两颗骰子，将骰子上的数字相加后再减去1（得出一个介于1和11之间的数字），将其作为浴缸中鱼的初始数量。我们将该数字称为N₀。玩家一从1到50之间选一个数字K，K 的数值决定每只鱼可产下多少只。如果最初浴缸中有N₀条鱼，那么，在第1年中，它们会产下（K/10）×N₀条鱼。因此，鱼群的数量将乘以K /10，即介于0.1与5之间的一个数字。

但并非所有新出生的鱼都能存活下来。假如前一年的年末共剩下N 条鱼，那么到了下一年的年末，鱼群数量将变为：

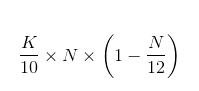
计算出的数值必须经过四舍五入，以整数表示鱼群数量（4.5只鱼即5条鱼）。

如此“运转”10年。奇数年份鱼缸中的鱼群数量即为玩家一的得分，偶数年份鱼缸中的鱼群数量则为玩家二的得分。(www.daowen.com)

设年份i 的鱼群数量为N_i, 那么，

玩家一的得分为：N₁+N₃+N₅+N₇+N₉

玩家二的得分为：N₂+N₄+N₆+N₈+N₁₀

在裁切出的鱼形上面，你可以写下每一年的鱼群数量。如果所有鱼只在某个年份全部死掉，那么，选择繁殖数量K 的玩家一便自动成为输家。

举例说明。玩家掷出两颗骰子，数字相加得四。因此，游戏开始时鱼缸中只有3条鱼：N₀=3。玩家一将数字K 设为20。因此，1年后鱼缸中的鱼群数量变为：

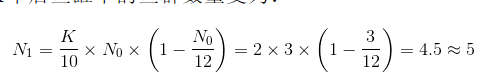
第2年后数量为：

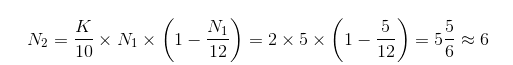
第3年后数量为：

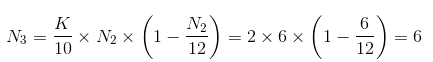
此时，鱼群数量将达到稳定状态，因为将数字6套进该公式后，所得出的结果仍然为6。因此：

玩家一得分：5+6+6+6+6=29条鱼

玩家二得分：6+6+6+6+6=30条鱼

所以玩家二获胜。接下来，改变一下乘数K 的值，看看会有什么变化。

因为在游戏里面，我们进行了四舍五入，因此结果并不十分精确，旅鼠种群中的那种混沌模型便不能在此起作用。

在这个线上模拟版本中，鱼群数量也同样进行了四舍五入，但分数部分则融入到下个年度的计算公式中。例如，如果将K 设为27，将N₀设为3。那么：

N₁=6.075，四舍五入得6条鱼。

N₂=8.09873，四舍五入得8条鱼。

N₃=7.10895，四舍五入得7条鱼。

N₄=7.8233，四舍五入得8条鱼。

N₅=7.352，四舍五入得7条鱼。

N₆=7.68872，四舍五入得8条鱼。

N₇=7.45835，四舍五入得7条鱼。

N₈=7.62147，四舍五入得8条鱼。

N₉=7.50844，四舍五入得8条鱼。

N₁₀=7.58804，四舍五入得8条鱼。

玩家一得分：6+7+7+7+8=35条鱼

玩家二得分：8+8+8+8+8=40条鱼