龙与地下城是20世纪70年代开始兴起的一款奇幻式角色扮演游戏，该游戏的一个奇妙之处是它提供了骰子组合。不过，游戏的发明者是否穷尽了所有可能的骰子呢？要了解什么形状才能制作出好的骰子，这就涉及我们在第2章中提出的问题。如果要求骰子的每个表面都一模一样，并均呈对称形状，同时，这些表面在衔接时，各个边角的构造都一模一样，这样的骰子共有5种，即5种柏拉图立体：正四面体、正立方体、正八面体、正十二面体及正二十面体。龙与地下城游戏中（以及本书网站上的相关PDF文件中）囊括了所有这五种骰子，但其中多数有着更加久远的历史。

例如，克里斯蒂拍卖行曾在2003年拍出过1枚古罗马时代玻璃制的二十面体骰子。这枚骰子的表面雕刻着一些奇怪的符号，暗示出它原本可能是用来算命的，而不是用在游戏中的。在当今最流行的算命游戏“魔法8号球”中，二十面体便位于中心位置。球内液体中浮着1个二十面体，其表面印有各种答案。游戏的玩法是：玩家提出1个问题，然后晃动魔法8号球。里面的二十面体便会漂浮至顶端，露出一个表面以给出相应的答案，其中包括“毫无疑问”、“不要期待”等各式答案。

如果你只想要1个公平的骰子，便无需对骰子表面的安排如此苛刻。例如，龙与地下城游戏中有一个用2个五边形底的金字塔拼贴出的骰子。这枚骰子每个三角形表面着地的概率均为10%。但它并非柏拉图立体（正多面体），因为每个金字塔的顶点不同于其他表面的顶点：前者由5个三角形组合而成，后者则由4个三角形相连而成。但这一点并不影响这枚骰子的公平性，因为其中每个表面着地的几率都是相同的。

数学家也对其他公平的骰子形状进行了研究。但直到最近，他们才证实出，在5种柏拉图立体——即5种终极性公平骰子的基础之上，还可以加入其他20种公平骰子（这些骰子仍然具有一定的对称性）。

而在这些新增的20种形状中，有13种是与足球形状相关的，即与第2章所提到的阿基米德立体（半正多面体）相关。阿基米德立体的表面都是对称的，但是，形状都不尽相同。尽管这些形状作为足球的形状很合适，但并不是很适合用来制作骰子。举例来说，经典足球有32个面，包括12个正五边形和20个正六边形。如果在这32个面上依次写下从1到32这些数字的话，我们就可以得到一枚公平的骰子吗？其中，每个五边形表面脱颖而出的几率为1.98%，而六边形表面的几率则为3.81%，因此这显然并不是公平的骰子。直到过去几年，数学家才研究出一个可以确定出足球骰子中五边形表面准确出现几率的公式。他们通过一些精彩的几何运算，最终得出以下这个令人望而却步的结果：

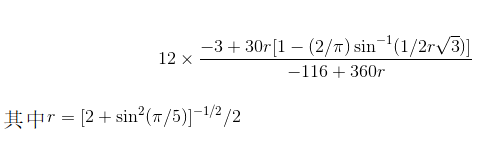
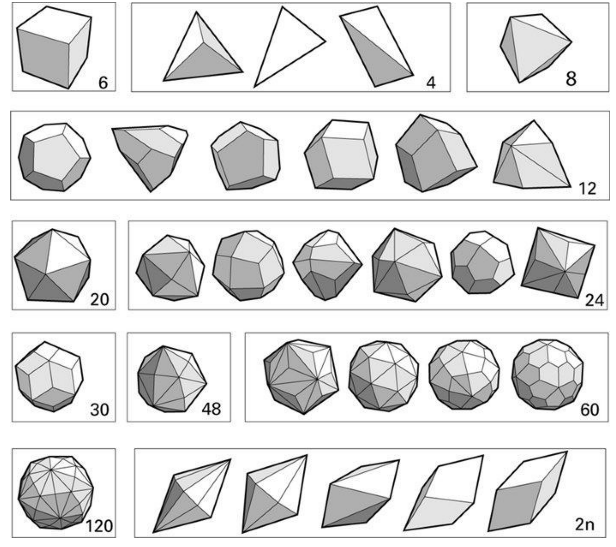
图 3-5　能够制造出公平骰子的对称形状

阿基米德立体本身并不是公平骰子的形状，但它们可用来构建出不同的形状，从而演变出一系列新的骰子，供玩家使用。关键的一点便是要意识到，尽管阿基米德立体中的每个表面都不相同，但每个顶点都如出一辙。因此，借助于一种名叫二象性的思路，我们可以把这些立体中的顶点变成表面，也可把表面变成顶点。经过这样的转换，我们会得到什么样的表面呢？请想象在每个顶点平放一张纸板，然后想象这些纸板彼此交叉或切入的情形。每张纸板都要调整到跟立体中心与顶点连线呈垂直的角度。例如，如果你用十二面体的表面替换其顶点，那么你就会得到一个二十面体（见图3-6）。(www.daowen.com)

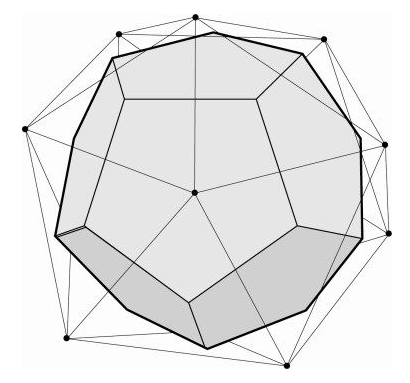
图　3-6

通过把这一思路运用在阿基米德立体上，我们可以得出13种新骰子。经典足球中共有60个顶点，而由此转化得出的骰子将有60个三角形表面，这些三角形不是等边三角形，而是等腰三角形（3条边中，只有2条边的长度相等）。尽管这一经典足球变体并非柏拉图立体，但是，这枚骰子的每个表面出现的几率都是相同的，即1/60，所以，它就是一枚十分公平的骰子，可供游戏玩家使用。它的学名是五角化十二面体（见图3-7）。

图　3-7

每一个阿基米德立体都能按照上述思路变换为一枚公平的骰子。其中最让人惊叹的则是六角化二十面体。尽管该立体包含120个不对称的直角三角形表面，但它却不可思议地构成了一枚公平骰子的形状。

而通过将两个金字塔形状拼接起来的方式可构建出无数种可能的骰子形状，因为金字塔底边的边数存在无数种可能性。尽管数学家们理出了对称形状的公平骰子的范围，但是，由更多不规则形状构成的公平骰子依旧是一个未解之谜。举例来说，如果我把一个正八面体的两个相对应的顶角分别切掉一点，便能创造出两个新的表面。而当我抛出这个立体后，它不太可能落在这些新表面上。但是，如果我切下一大块，这两个新表面比其他八个表面落地的机会就更大。在这两个极端之间，势必存在某个交汇点，可使两个新表面与剩余八个表面落地的概率达到一致，如果这样的话，一枚由10个表面构成的骰子便诞生了。

它的形状并不像阿基米德足球变形得出的新骰子那样有美妙的对称感，但它同样可构造出公平的骰子。对于以类似方式构造出公平骰子，数学家尚未掌握全部答案，我们仍在努力寻找一种方式，以便有效地囊括所有类似的骰子形状，并最终构造出公平骰子。