古代人认为地球是平的。但是，随着人类开始去远方旅行，了解地球的总体形状就显得更加重要。假如地球是平的，那么，大家都认为，如果你离开得够远，就会从地球的边界上掉下去，除非这个世界无穷无尽，你永远都不能到达边界。

许多文明都逐渐认识到，地球最可能的形状应该是弯曲的，而且是有尽头的。在所有的推测中，最明显的一个当然是球形，而且一些古代数学家仅通过对一天光影变化的分析就精确地计算出了地球的尺寸。但是，为何科学家能如此确定，地球的表面不是被包裹在其他有趣的形状内呢？他们怎么知道我们不是居住在一个圆环体的表面之上，就像雅达利游戏中的太空人被禁锢在一个百吉饼式的宇宙之中呢？

其中一种探寻方式就是在其他可选择的世界中展开一场想象的旅程。那么，设想让一位探险家置身某个星球中，而且告诉他这座星球要么是一个完美球形，要么是一个完美圆环体。他如何辨别这二者之间的区别呢？我们先让他沿着一条直线穿越这个星球的表面，同时交给他一把刷子和一桶白漆，用来标记他走过的路线。最后，他会回到起始点，而他的足迹便构成了围绕该星球的一个巨大的白色圆圈。

现在，我们再交给他一桶黑漆，并告诉他要沿着另外一个方向走。在球形的地球上，不管他选择什么方向，在他回到原点之前，黑线总会和白线相交。要记得探险家总是沿着表面上的直线行走，因此，这一交汇点必将是星球另一端和出发点相对的那个点。

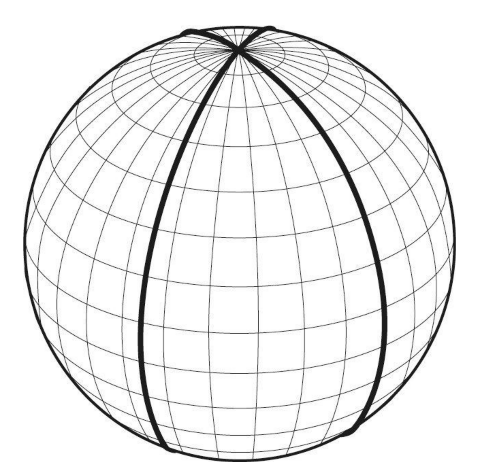
图 2-41　球形上的两条路线交汇在两个点上

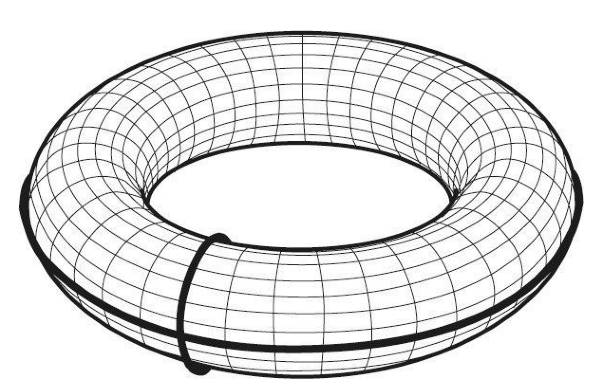
图 2-42　圆环体上的两条路线只交汇在一个点上

若探险家在一个圆环体的星球表面上行走，情况就会完全不同。白色线路会带领探险家绕着圆环体的内圈行走，穿过圆环上的洞口，并从另一侧走出。但是，若把黑色路线设为与白色路线垂直，他便会在圆环体的外围绕上一圈，而不会绕着圆环体内圈行走。因此，两条路线有可能只在出发点交汇一次。

问题是星球表面通常并非完美球形，亦非完美圆环体，其形状常常是畸形的。曾被陨石击中的陨石坑令地面发生了变形，因此，当探险家沿直线行走遇到一个深坑或凸丘时，他就不得不偏离原来的轨迹。事实上，如果探险家沿着直线一直走，他很有可能半途遇险，永远回不到出发点。既然凹形只是某些扭曲的球形或圆环体，是否还存在其他什么方法能够把它们区分出来？此时，便可突显出拓扑学的强大了，因为在拓扑学的眼中，重要的不是两点间什么路线最短，而是一条路线能否变为另外一条路线。

现在，让我们的探险家重新再走一遍，但这次不用油漆，改用白色松紧绳。先让他拉着白色绳子走一圈，返回原点后用绳子的两端打上结，因此，这就像是给这个星球上了套索。然后再让他拉着黑色松紧绳沿另一条路线走一圈，完成后同样把绳子的两端打上结。如果这个星球基本是个球形，只有少数凸起或凹陷，那么无需切断绳子便可将黑色绳子完全重合到白色绳子上。但是，如果行星为圆环体形状，上述操作就不一定总是可行。如果黑色绳子绕向圆环体的内环，而白色绳子沿着外环绕了一圈，那么便无法在不切断绳子的前提下把黑色绳子合并到白色绳子上。这样一来，探险家仅通过在行星表面旅行而无需离开地表便可判断出该行星上到底存不存在洞口了。(www.daowen.com)

另外，还有两种有趣的方法，可用来区分这个星球是圆环体还是球形。设想这两种星球上均布满皮毛。若探险家行走在圆环体星球上，他就会发现，他能够把这个星球表面上的所有皮毛都均匀地梳向一边，比如，他可以把所有皮毛先向着洞口的方向梳倒，然后一直顺着洞口就能从背面梳回来，这样就能一路把皮毛全都梳倒。但是，若行走在球形的星球上，他就会遇到麻烦。不管他如何梳理这些皮毛，最终总会有一小块区域的皮毛是竖着的。

由此可以得出一个怪异的有关这两种形状的星球天气的推论，因为皮毛的倒下象征着风吹过的结果。在球形星球中，总会有什么地方（皮毛竖着的地方）是风吹不到的，而在圆环体星球上，风可以吹到表面所有的地方。

这两种星球的另一个不同之处则体现在它们各自的地图上。在每个形状的星球上划分出许多国家，然后，用不同颜色把这些国家标出来，使任何相邻国家的颜色都不一样。在一个球形星球的表面上，只需4种不同颜色就可以做到这一点。以欧洲地图为例，卢森堡被德国、法国和比利时包围，因此我们至少需要4种颜色。但奇妙的是，四种颜色就足够了，再多一种也不需要。不管你如何划分这些欧洲国家的边界，制图师永远不需要第五种颜色。但是，要证明这一现象并不容易。为了证明绝不存在需要第五种颜色的疯狂地图这一现象，人类不得不诉诸于电脑，这也是人类最早借助电脑求解的数学问题之一。因为要证明这一点，需要检验数以千计的地图，仅仅依靠手工的话，作业量实在太大。

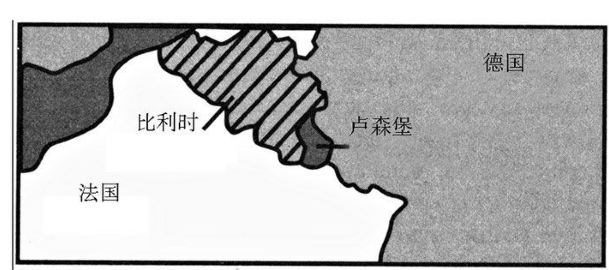
图 2-43　为欧洲地图上色只需4种颜色

那么，对于生活在一个圆环体星球上的制图师来说，他需要动用多少种颜色呢？答案是最多7种。我们来回顾一下雅达利游戏中的宇宙，它是由1个长方形荧屏卷曲而成的。首先，我们把屏幕上方和下方接起来，卷成1个圆筒，然后再将圆筒的左边和右边接起来，从而构成1个圆环体。图2-45所示便是一张尚未卷曲起来的圆环体表面地图，一旦将其完整连接后，则需要7种颜色。

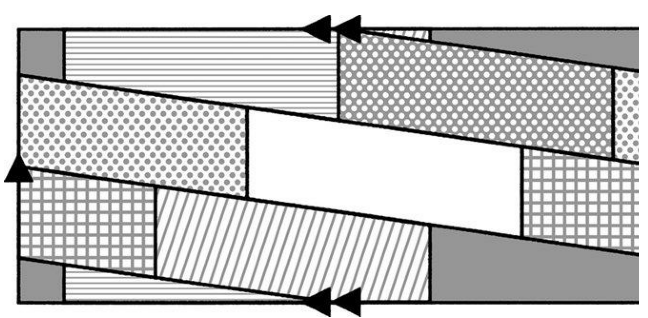
图 2-44　将上述地图的上下和左右两端连接起来构成一个圆环体后，你就会发现该图需要用7种颜色来上色

至此，我们一路了解了与气泡、圆环体、分形及泡沫相关的各种数学问题，现在，就让我们来面对数学中的形状这个终极问题吧。