1979年，游戏机公司雅达利（Atari）发布了最受玩家欢迎的一款游戏《爆破彗星》。游戏玩法是击毁空间中的小行星和飞碟，以免在飞行过程中遭到撞击，或遭到飞碟的火力攻击。该游戏的街机版本在美国大获成功，游戏公司不得不为街机安装更大容量的游戏币储存空间，以使每台机器可以接收到大量游戏币。

不过，当我们以一种数学观点来观察该游戏的几何形状时，便会发现其中十分有趣的地方：当飞船从屏幕上方消失后，它又神奇地出现在屏幕的下方。同样地，当你操作的飞船从屏幕左侧飞出时，它又会立刻出现在屏幕右侧。接下来发生的事情就是太空人完全被限制在这个二维世界中，屏幕中的图景便是整个宇宙。尽管这是一个有限的宇宙，但是，它并没有边界。因为太空人永远不会撞到边界线，他飞来飞去的地方并非一个长方形，而是一个更有意思的宇宙。那么，这个宇宙到底是什么形状的呢？我们能否将其描述出来呢？

如果太空人从屏幕上方飞出然后立刻出现在屏幕下方，那么，这说明宇宙中的这两个部分一定是连接在一起的。假设计算机屏幕是用弹性橡胶制成的，我们便可将其卷曲起来，使其顶部和底部连在一起。当太空人纵向飞行时，我们就能看到，他实际上是在围绕圆柱体飞行。

那么，另外一个方向上又是什么呢？因为当飞船从屏幕的左侧飞出后，会马上进入屏幕右侧，所以，这个圆柱体的两端也必须是相连的。如果把所有应当相连的点都标记出来，我们就会发现，必须要把圆柱体弯成圆形，而且要使其顶端和底端连接在一起才行。由此可见，我们的太空人所身居的宇宙实际上是个甜甜圈的样子，或者数学家认为的圆环体。

上述我用一块橡胶来论证宇宙形状的方法，实际上是数学家在100年前开始观察形状的一种方式。对古希腊人来说，几何（几何的英文词条Geometry便源于希腊语，原意为“测量地球”）是关于计算点和角度之间的距离的一门学问。然而，对于游戏中太空人的宇宙形状的分析，更重要的是与它的整体连接方式相关，而非与太空人的宇宙中的实际距离相关。这种全新的观察形状的方式便是拓扑学。借助于这种新方式，我可以将其假想为橡胶或橡皮泥制品，随意地对其弯曲和连接。

很多人每天都在使用拓扑地图。你能认出下面这张图是什么地图吗？这是一张伦敦地铁系统的地理路线图。尽管这张图在地理上是准确的，但使用起来很不方便。因此，伦敦人现在主要使用的是拓扑地铁地图。这类地图最早由哈里·贝克在1933年设计，他把地理路线图拉直铺开，从而使用起来更加方便。如今，这类地图已经遍布世界各地。

图 2-38　伦敦地铁的地理路线图(www.daowen.com)

要弄清楚能否解开一个绳结，这也是拓扑学上的一个问题，因为在解绳的过程中，我们可以把绳子绕来绕去，而无需将其剪断。这一点对于生物学家和化学家来说是极为重要的，因为人类的DNA往往会缠绕成奇怪的结。有些疾病，比如老年痴呆症，可能就与DNA的打结方式存在联系，而数学则具备解开这些谜团的潜能。

20世纪初期，法国数学家昂利·庞加莱开始思索，以拓扑学的观点来看，世界上到底存在多少种不同的表面结构。这就像是寻找雅达利游戏中的二维太空人所能栖居其间的所有形状。庞加莱的兴趣在于以拓扑视角来观察这些宇宙，如果两个宇宙无需裁剪就能转换为彼此的形状，那么这两个宇宙便可被视为相同的宇宙。比如，一个球体的二维表面在拓扑范畴上等同于一个橄榄球的二维表面，因为这二者可以互相变换。但是，这个球形宇宙和雅达利游戏中太空人飞来飞去的圆环体则分属不同的拓扑形状，因为在没有裁剪和粘贴的情况下，我们无法把一个球体变换为一个甜甜圈的样子。那么，其他形状都是什么样的呢？

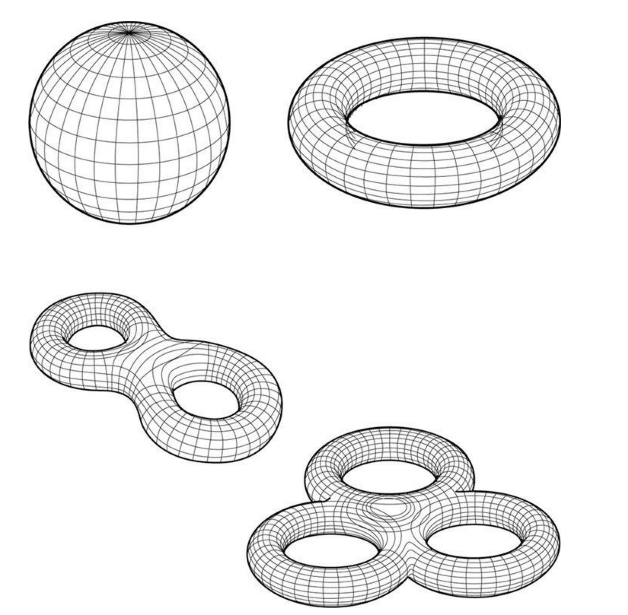
图 2-39　昂利·庞加莱发现拓扑分类中的前4个形状，在该分类中，庞加莱给出了各种将二维平面折叠起来的方式

庞加莱证明出，无论一个形状有多么复杂，它最终总是可以变换为下列形状中的一种：球体、单洞圆环体、双洞圆环体、三洞圆环体，以及包含任何有限数量洞口的圆环体。从拓扑学的观点来看，这就是雅达利太空人栖居其中的所有可能的宇宙形状。形状的特征由洞（数学家称之为属）的数量决定。比如，茶杯在拓扑学上等同于一个百吉饼，因为两者均只有一个洞口。茶壶上则有两个洞，一个在壶口，一个在壶盖，因此它能够变换为一个双圈饼干的模样。图2-40中的形状可能更难理解一些，这个形状中有两个洞，因此可以变换为一块双圈饼干的模样。但由于图中两个圆环套在一起，看上去似乎一定要动用剪刀才能使其成功变换，但其实并不需要。本章结尾处，我会揭示如何不用剪切就能把这对圆环解开。

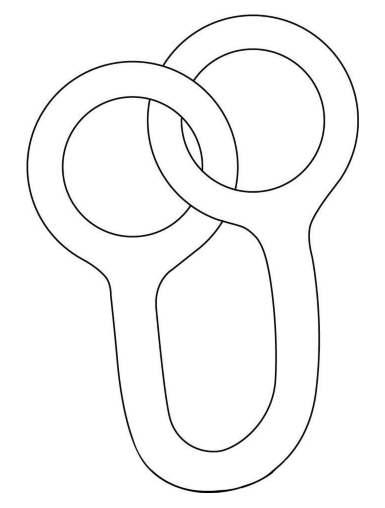
图 2-40　如何通过持续变形，在不动用剪刀的情况下，将两个彼此相扣的圆环解开