分形出现以前，数学家们所接触的形状都是单维、二维或三维的。单维的直线，二维的六边形，三维的立方体，诸如此类。但是，分形理论中的一个了不起的发现便是，这些形状的维度竟然大于1但小于2。此刻，你如果战力十足的话，就让我们一起来看一下，一个形状如何能够实现大于1但小于2的维度。

其中的把戏就是提出一种聪明的方式来区分为何直线是单维的，而正方形却是二维的。想象一张透明的方格纸，将其放置在某个形状上面，数出与该形状交汇的方格数量。接着，再拿来另一张方格纸，而这次纸上的格子尺寸为刚才那张纸上的一半。

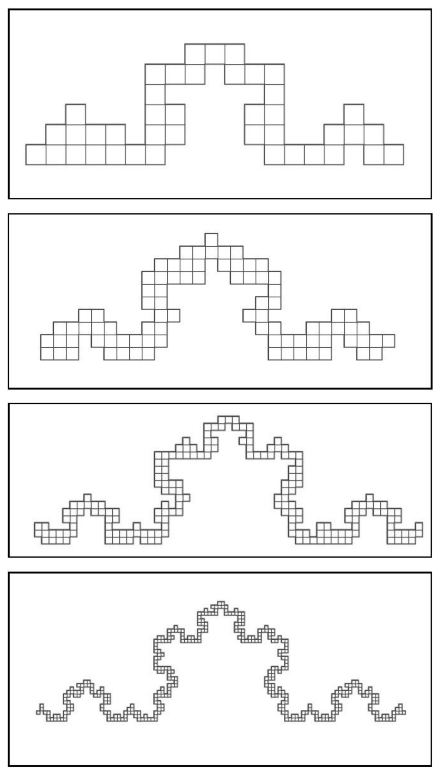
图 2-31　这几幅图描绘了使用方格纸计算分形维度的方法。随着像素尺寸的缩小，像素数量增加的比率便对应其分形维度

如果这个形状为一条直线，那么测量出的方格数量则直接变为之前的两倍。如果形状为正方形，那么，测出的方格数量则为之前的4倍，即2²倍。每次采用尺寸折半的方格纸来测量单维形状所得的结果都是之前结果的2——即2¹倍，而每次测量二维形状的结果则为之前结果的2²倍。可见，维度值所对应的便是2的幂数。

有趣的是，当我们把这一程序套在之前我们创建出的分形海岸线上时，方格尺寸折半以后，所得出的测量结果大约为之前结果的2^1.26倍。所以，从这个角度来看，可以将这条数学上的海岸线维度视为1.26。如此，我们便创造出了一种对于维度的新定义。

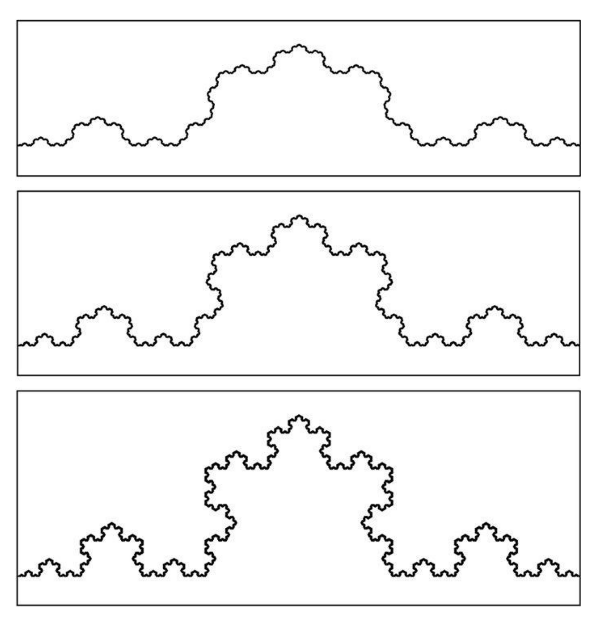
不用网格纸的话，通过像素化的电脑屏幕也可以捕捉到这些形状。将包含该形状的像素设成黑色，反之则为白色。当我们将屏幕分辨率调高，对应黑色像素增长的维度便凸显了出来。比如，将16×16的像素调为32×32以后，对一条直线来说，黑色像素的数量增加了一倍；而对一个正方形来说，黑色像素的数量增加为原来的4倍，即2²倍；当使用此方法测量科赫曲线时，所得出的结果则为之前的2^1.26倍。

(www.daowen.com)

从某个方面来讲，该维度向我们呈现了该曲线试图占据的空间大小。如果我们换一种方式来创建分形海岸线，通过改变取而代之的两条线之间的角度，使该角度越来越小，那么所对应的海岸线便会填满越来越多的空间。而当我们依序测量这些海岸线变体的维度时，则会发现它们的维度会越来越接近于2（如图2-32所示）。

图 2-32　随着三角形的角度变化，所得的分形会填满越来越多的空间，同时，其分形维度也随之增加

在分析自然形状中的分形维度时，一些有趣的事情会凸显出来。英国海岸线的分形维度据估计约为1.25——十分接近于我们所创建的数学海岸线的维度。使用越来越精密的测量仪器后，海岸线长度的增长速度会有多快，看其分形维度就清楚了。澳大利亚海岸线的分型维度据估计为1.13，说明它相对英国海岸线来说，复杂度较小。而惊人的则是南非的海岸线，其维度仅仅为1.04，这说明其海岸线相当圆滑平顺。最复杂的海岸线可能要属挪威了，算上该国的所有峡湾，挪威海岸线的分形维度高达1.52。

图 2-33　英国海岸线的维度是多少

而对于三维立体来说，我们也可以想象一个类似的流程，运用立方体网格来代替方格纸，然后逐次缩小网格的尺寸，观察所测量的形状与网格的交汇情况。借助于这样的流程，花菜形状的维度是2.33；纸团的维度是2.5；西兰花则更加复杂，维度达到2.66；更加惊人的则是人类的肺，分形维度高达2.97。