英国的海岸线是18 000公里吗？还是36 000公里？还是更长？令人惊讶的是，这个问题的答案并不明确，回答这一问题要与人类直到20世纪中叶才发现的一种数学形状有关。

当然，由于每天两次的潮起潮落，英国的海岸线长度也在不停地变化。但是，即使我们把海岸线完全固定下来，它到底有多长仍然不是那么明确。这里面的微妙之处就要看你的测量到底有多精确。如果你用一根根直尺首尾相连地测量海岸线，然后再数从头到尾用了多少根直尺，这样做必然会漏掉许多无法测量的细微之处。

如果你用一根很长的绳子来代替直尺的话，那么，你能测量出海岸线上众多错综复杂的形状的长度。当你拉直绳子再进行测量时，你就会发现这次的结果比之前按照直尺测量出的长度要长很多。

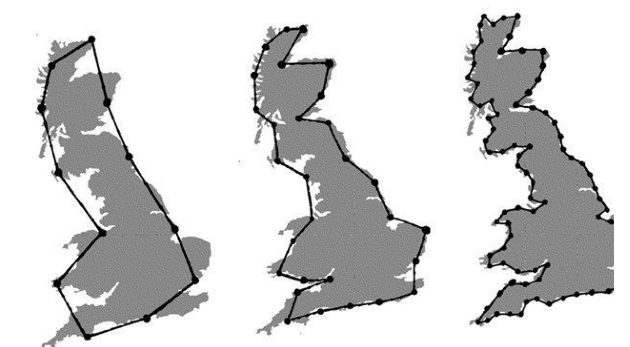
图 2-21　 测量英国海岸线

但是，由于绳子的灵活性存在局限，它无法很好地捕捉到海岸线上1厘米以内的弯度。如果改用一根细线，我们就能捕捉到更多类似的细微之处，从而使测量出的海岸线的长度进一步变长。

英国地形测量局公布的英国海岸线长度为17 819.88千米。但是，如果我们测量得再细致一些，把更细微的部分度量进去，就能得到两倍于此的数字。从以下事例中我们便能看出度量地理界线的长度有多么困难了：1961年，葡萄牙方面宣称它与西班牙交界的边界长度为1220公里，而西班牙方面提供的数据则为990公里。类似的差异也出现在荷兰和比利时之间的边界长度上。一般来说，较小的国家测出的边界线总是更长些……

因此，这样一味细致下去到底有没有极限呢？也许测量得越细致，海岸线的长度就会越长。为说明这一点，让我们来打造一条数学上的海岸线。为画出这条海岸线，你需要一个毛线球。你从中拉出1米长度的线，拉直了平铺在地板上。

图　2-22

真实的海岸线当然不可能这么笔直，于是，我们向内做一个大凹槽。继续从线球拉伸出一定长度的线，直到地上笔直的海岸线中段三分之一变成向内凹进的两个与之前中段相等长度的边为止，如图2-23所示。

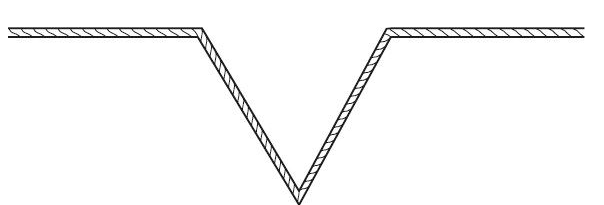
图　2-23

那么，这一次到底要从线圈中拉出多长的线呢？我们知道第1条线由三段⅓米长的线段组成，而第2条新海岸则包括4条⅓米长的线段。因此第2条的长度便是第一条的4/3倍，即4/3米。

但是，第2条线依旧不够复杂。于是，让我们继续重复以上操作，将每一段短线都一分为三，再把中间一段以两个相同长度的边取代。如图2-24所示。

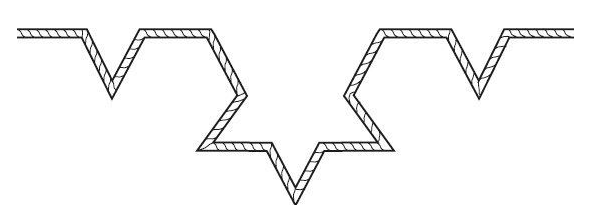
图　2-24(www.daowen.com)

现在，这条海岸线有多长呢？其中，四段线中每一段的长度都增加为原先的4/3倍，因此，此时海岸线的长度变为了（4/3 × 4/3）m = (4/3)² m。

可能你已经猜到我们接下来要做什么了。没错，持续重复这个步骤，不断地把线段一分为三，然后以两条同等长度的边线来代替中间的一段。每这么做一次，线条的长度便增加为原来的4/3倍。100次以后，海岸线的长度将变为原来的(4/3)¹⁰⁰倍，算下来是刚刚超过30亿千米。将这样一根线拉直以后，它可以从地球一直延伸到土星上。

只要我们无限重复这个步骤，就会得到无限长的海岸线。当然，物理学法则使我们的拆分流程无法超过某个特定限度（这一限度由普朗克常数决定）。因为物理学家告诉我们，若一段距离小于10^-34m，它便超出了可测量的极限，否则就会出现黑洞，而黑洞将吞没测量设备。当我们不断重复以上把戏，在进行到第72次之前，线段的长度就已经小于10^-34米了。不过，数学毕竟不是物理。在数学的世界中，我们完全可以无限度地拆分一条线，无需担心堕入到黑洞之中。

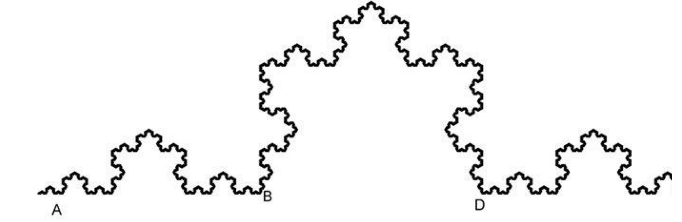
图 2-25　将AB之间的分形放大3倍便可得到以上完整分形。而完整分形同样可以由4个AB之间的小分形拼凑而成

另一种认为海岸线为何无穷无尽的方法是在上图中思考AB间这段海岸线。假设其长度为L。如果我们将该段海岸放大3倍，所得到的结果和AE之间的海岸线一模一样。因此整段海岸线的长度便是3L。但从另一个角度来看，如果我们把4份这样的AB小段首尾相连，便刚好能覆盖掉整段海岸线：AB、BC、CD以及DE。这样的话，整段海岸线的长度则是4L，因为我们需要4个小段来拼凑出整段海岸线。但是，不管我们以何种角度来测量整段海岸线的长度，所得出的结果都应该是一样的。那么，怎么才能让4L=3L呢？求解该等式，L的值只有两种可能，或者为零，或者无穷大。

上述这段无限长的海岸线实际上是科赫曲线形状的一条边。瑞典数学家海里格·冯·科赫在20世纪初构造出这一形状，因此，它也被称为科赫曲线（如图2-26所示）。

图　2-26

由于这个数学形状的对称性太强，所以，它并不像是一条真正的海岸线，而且，它看上去也不是很自然或很不可分割，但是，如果在每次进行拆分操作时把2个边的向外突出改为随机向内或向外突出，效果看上去就显得更加自然和可信了。图2-27便是通过相同的操作，但在决定向内或向外突出时听从于一枚硬币的决定所得出的图形。

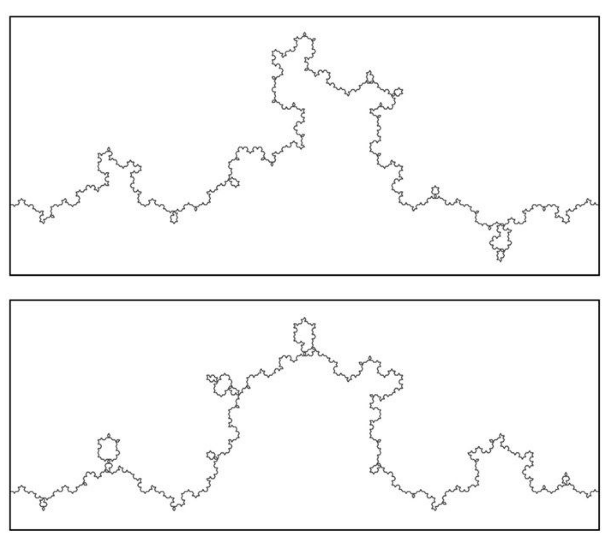
图　2-27

如果把几段这样的海岸线连接起来，整个形状看上去就非常像中世纪时期的英国地图。

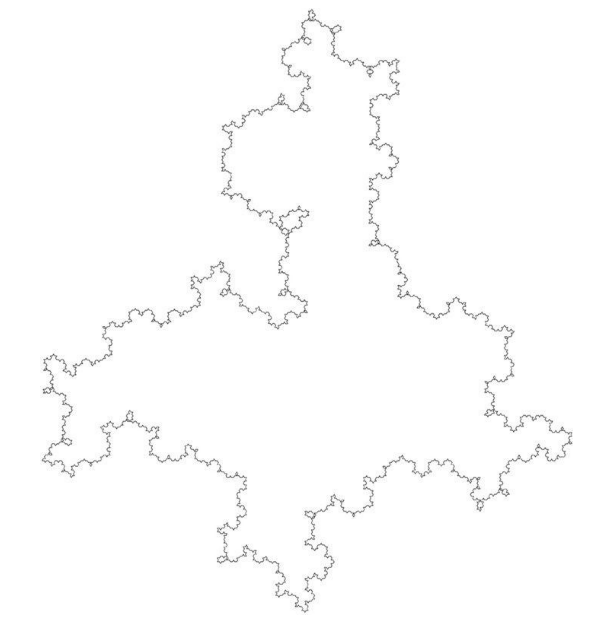
图　2-28

综上所述，如果有人问你英国海岸线的长度，坦率地说，你想给什么答案都行。这不就是我们上学时人人都期待的那种考题吗？