北京奥运游泳中心是一座不同凡响的精美建筑，特别是入夜后，华灯初上，它看上去就像一只充满气泡的透明盒子。其设计者Arup（英国奥雅纳工程顾问公司）力图捕捉到在室内举行的水上运动的精神，同时，还想使这个建筑物具备一种自然有机的外观。

一开始，他们试图在垒完的墙壁中寻找一些形状，比如正方形、等边三角形或六边形等，但他们认为这些形状都太过常规，不足以捕捉到他们所追求的那种有机感。随后，他们开始探寻自然界中堆叠事物的方法，比如水晶，或植物组织中的细胞结构等。在所有这些结构中（包括类似阿基米德所发现的用来制作足球的一类形状）最吸引Arup的则是泡沫中众多气泡叠加在一起所组成的形状。

将多个气泡叠加起来制成泡沫，便可引出一个至今依然折磨着数学家们的难题，鉴于人类直到1884年才证实对单一气泡来说，球体是其中最高效的一种形状，泡沫对于数学家们的困扰也就不足为怪了。如果两个含有相同空气的气泡聚在一起，它们将组成哪种形状呢？这里面的规则依然要建立在气泡十分懒惰这一点之上，它们永远会寻求消耗最少能量的那种形状。由于能量的消耗和表面面积成正比，因此，它们试图构成的形状也将含有最小的肥皂泡表面区域。由于两个聚在一起的气泡会共用同一块表面，它们最终所构成的形状的表面面积将比两个刚刚触碰的气泡的表面面积还要小。

吹泡泡的时候，如果两个相同体积的气泡组合在一起，它们构成的结构将如图2-9所示。

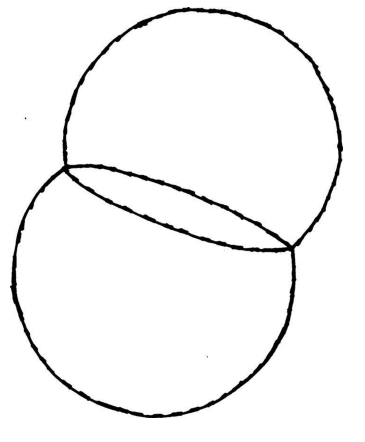
图　2-9

两个不完整的球形以120度的角度结合在一起，共用同一个内部平面。这当然是一种稳定状态，如果不稳定，自然自会让它们的形状发生变化。但问题是，是否存在另外一种表面面积更小的形状，从而消耗更少的能量，使其更加高效呢？要使气泡摆脱当前的稳定状态，或许需要注入一些额外的能量，不过，也可能存在另外一种可能的形状，使两个触碰的气泡承担更少的能量。或许两个气泡能以某些怪异的结构聚合起来，比如其中一个气泡变成甜甜圈的样子把另一个气泡包裹在内，构成一种类似落花生的形状（如图2-10所示）。

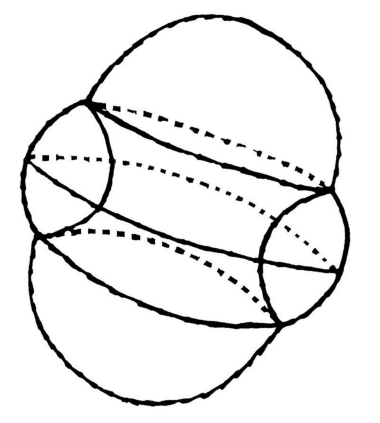
图　2-10

更好的气泡聚合方式终究是不存在的，对于这一点的首次论证发表于1995年。虽然数学家并不乐于求助电脑，因为电脑中没有他们所中意的美妙与精巧，但是，他们还是需要在电脑的帮助下执行证明过程所涉及的复杂数学运算。

5年后，一份关于双气泡聚合的手写证据发表了。它实际上证明了一种更加常见的聚合形式：2个体积不同的气泡聚合起来时所共用的内壁不是平面的，而是向较大气泡方向凸起的1个曲面。该曲面实际上属于另外一个球形的表面，交汇的三张肥皂薄膜彼此之间的角度均为120度（如图2-11及图2-12所示）。

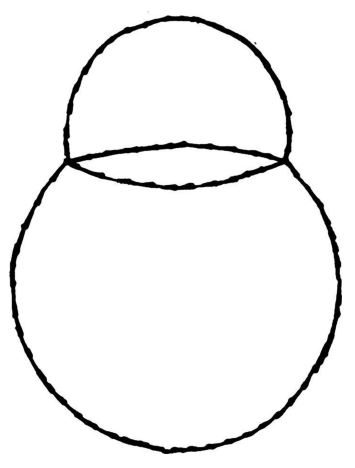
图　2-11

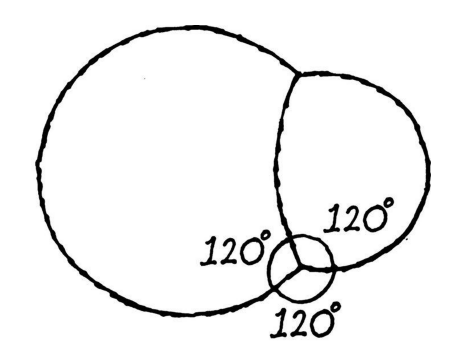
图　2-12

实际上，120度是所有泡沫聚合时的一个通行角度。最初揭示这一点的是生于1801年的比利时科学家约瑟夫·普拉托。当时，他正研究光线照射眼睛时所产生的效应，为此，他曾直视太阳长达半分钟的时间。40岁时约瑟夫双目失明，此后，在亲人同事的帮助下，他转向研究气泡的形状。

一开始，普拉托是通过将铁丝框架浸入肥皂水中来观察气泡最终呈现的形状的。比如，将1个立方体造型的框架浸入肥皂水后会得到13张泡沫壁，这些泡沫壁的交汇处会在立方体中构成1个小立方体（如图2-13所示）。

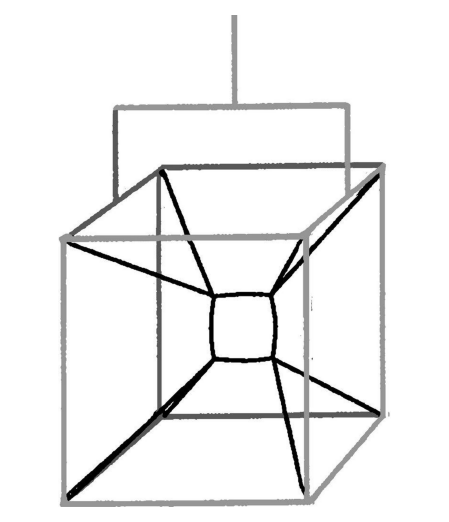
图　2-13

实际上，它并非一个真正的立方体，因为它的每个边都向外凸出。随着普拉托探索了各种各样的铁丝框架以后，他逐渐发现了气泡聚合时的一系列法则。

第一条法则，泡沫薄膜总是三个三个地聚合在一起，且彼此之间均呈120度的角度。为表示对普拉托所做贡献的敬意，这种由3片薄膜相交所得的线条被称为普拉托边界。第二条法则是关于这些边界的交汇方式。4条普拉托边界交汇时所构成的角度为109.47度（精确地说，为cos1/3）。以四面体为例，从每个顶点向四面体中心连线，即可得到泡沫中的四条普拉托边界交汇时的布局结构（如图2-14所示）。因此，立方体框架中的那个4边凸起的方块中每个边角的角度实际上都是109.47度。任何不满足普拉托定律的气泡都是不稳定的，从而会继续活动以演变为一个最终满足这些法则的稳定结构。直到1976年，简·泰勒才最终证实泡沫中的气泡必须满足普拉托定下的这些法则。她的研究告诉了我们气泡之间的连接方式，但是，泡沫中的气泡的真实形状究竟是哪种呢？由于气泡十分懒惰，要回答这个问题，就要找到这样一种形状，在泡沫中每个气泡封存一定量空气的前提下，肥皂薄膜的表面面积达到最小。(www.daowen.com)

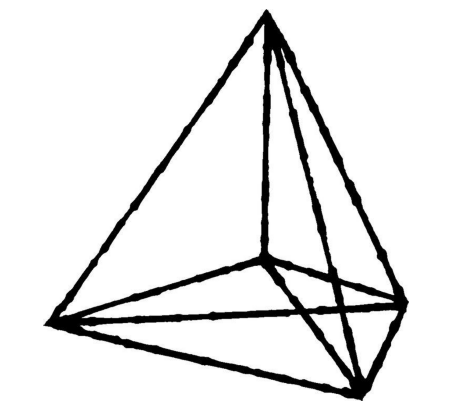
图　2-14

蜜蜂已在二维空间中给出了这个问题的答案。蜜蜂之所以使用六面体结构来建设蜂巢，是因为在每个蜂巢封存一定量蜂蜜的前提下，这种结构能够确保使用蜂蜡的分量最少。不过，最近的一项研究突破才证实了蜂巢理论：没有比六面体的蜂巢更加高效的二维结构了。

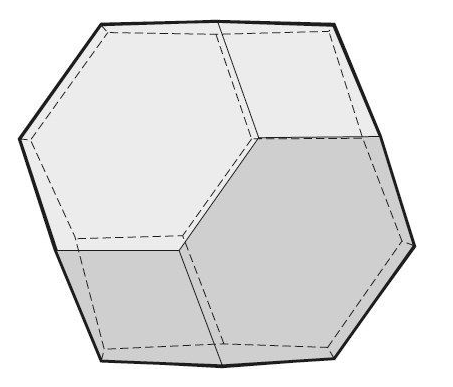
图　2-15

但当我们转而面对三维结构时，情况就没有这么明确了。1887年，著名的英国物理学家开尔文男爵认为其中一个阿基米德足球形状便是解决泡沫表面面积最小问题的关键。他认为，尽管六边形是构成高效蜂巢的基础，但构成泡沫的关键组件则是去顶八面体——将标准八面体的6个角都削掉后所得出的形状。

普拉托为气泡聚合模式所订立的法则显示边线和表面都不是平直的，而是弯曲的。例如，正方形四个角的角度为90度，但根据普拉托第二条法则，这一点在泡沫中并不成立。正如立方体框架中的方块所呈现出的，其四条边均向外凸起。因此，那两片肥皂薄膜交汇的角度则应是109.47度。

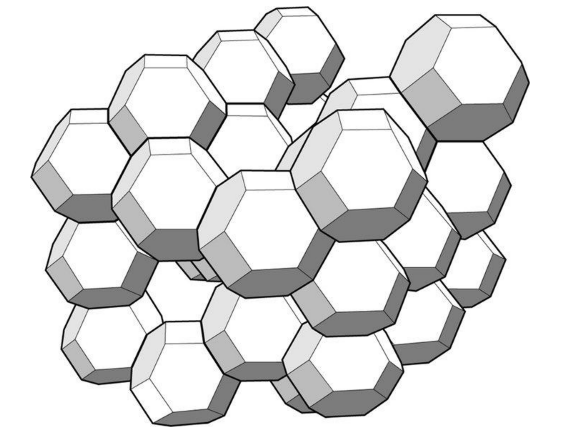
图 2-16　由去顶八面体所构成的泡沫

图 2-17　丹尼斯·维埃尔和罗伯特·费兰所发现的造型

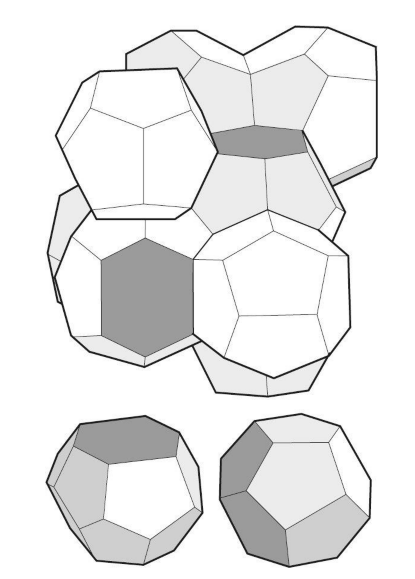
许多人相信开尔文给出的结构一定就是最小表面积气泡的真实形状，但没人能够证明这一点。1993年，都柏林大学的丹尼斯·维埃尔和罗伯特·费兰发现了两种新形状，把它们组合起来后比开尔文的结构还要节省0.3%的面积（这对于所有那些认为数学证明不过是浪费时间的人来说，无疑是当头一棒）。

结果证明，这些形状并不在阿基米德的列表上：第一种形状是由不规则的五边形所构成的不规则的十二面体；第二种形状是一个由2个拉长的六边形表面和12个不规则的两种五边形表面所构成的十四面体。维埃尔和费兰发现，他们能把这两种形状组合起来，从而创造出一种比开尔文提出的还要高效的泡沫结构。另外，为了满足普拉托定律，结构中的边界线和表面均设成了弯曲状态，而非平直状态。有趣的是，人们很难直接进入泡沫内部去观察其真实的结构，但是，多亏了这两位科学家借助于计算机模拟泡沫而做了各种实验，最终才发现了这两种形状。

但这是否就是气泡呈现的最好形状了呢？对此，我们无从得知。我们相信，这应该就是气泡最高效的一种形状系统。但在那时，开尔文以为他已找到了答案。

Arup的设计师们为了呼应奥林匹克游泳场馆内举行的水上运动而寻找有趣的自然形状时，一直在观察雾气、冰川和波浪。当他们偶然发现维埃尔和费兰发现的泡沫形状时，就意识到他们将有可能创造出建筑界从未应用过的什么东西。为创造出不太规则的形状结构，他们决定从某个角度切开一块泡沫。当我们近距离观察水立方（北京奥林匹克运动会游泳场馆的正式名称）的外侧时，它看上去就像用一块玻璃横截开泡沫时气泡所呈现的形状。

图 2-18　水立方的外观仿佛是一些不太稳固的气泡

尽管Arup的建筑结构看似随机，但从整个建筑的角度来看，其中还是存在某些结构的重复，但这已足够营造出他们所追求的有机感了。如果你仔细地观察，其中有一个气泡似乎并没有满足普拉托定律，除了呈现出普拉托法则中规定的120度和109.47度以外，它还呈现出一个90度的直角。这么说来，水立方还稳固吗？当然，如果它真由气泡建成，答案将是否定的。那个直角气泡必须要改变形状以满足所有气泡都必须遵守的数学法则。但是，我们无需担心。凭借隐藏于这一美妙结构背后的数学运算，水立方是会稳固矗立下去的。

对众多气泡的聚合感兴趣的并非只有Arup和中国有关部门而已。理解泡沫结构帮助我们弄清楚自然界中的许多其他结构的形状，比如植物细胞的结构、巧克力和奶油的结构、啤酒沫的结构等等。泡沫可用于灭火、保护水源免受泄露的放射性物质的污染，也可用于采矿等。不管你喜欢玩火，还是想知道为何杯中吉尼斯黑啤的泡沫会经久不息，答案都建立在对泡沫数学结构的理解之上。