第二节　实验室中的提取行为

1.被试与实验场景

我们从印第安纳大学本科生挑选实验被试。自愿参与的学生主要来自经济学学科。在招募以前，我们向潜在的志愿者们做了简要解释，只说他们将在“经济选择情境”下作出决策，而且他们将赚到的钱取决于他们自己的投资决策与实验小组其他人的投资决策。全部实验都在印第安纳大学NovaNET计算机系统进行。计算机为实验的统计程序提供了便利，加强了实验控制与被试控制，并大大减少了实验对实验者的人数要求。

在每个实验开始时，我们告诉实验被试:(1)他们要作出一系列投资决策;(2)所有的个人投资决策对群体保密;(3)他们将在实验结束时得到自己的收入(私下进行且是现金支付)。然后，被试按照描述决策的指示，以自己的节奏进行实验。^[2]

被试要遵循下列指示:他们在每个决策轮得到一定量的代币，并可以把代币投资到两个市场。市场1代表的投资机会，每个代币有固定的产出率，每产出单位生产固定的回报。市场2(公共池塘资源)所生产的每代币产出率取决于整个群体所投资的代币总量。我们用函数与表格来描述每个群体投资的产出率。被试知道，他们从市场2得到的产出水平，等于他们投资的代币量在群体总投资代币量中所占的比例。而且，被试知道市场2的每单位产出对应固定比例的回报。图5.1是对被试在实验中看到的实际信息的总结。被试确切地知道群体中决策者的总数、群体拥有的代币总数，而且知道实验者给每个被试的代币数是相同的。他们知道实验过程将不超过两个小时，但不知道会进行多少轮投资决策。所有被试都是有经验的，即他们至少已经参与过一个运用这种决策情境形式的实验。^[3]

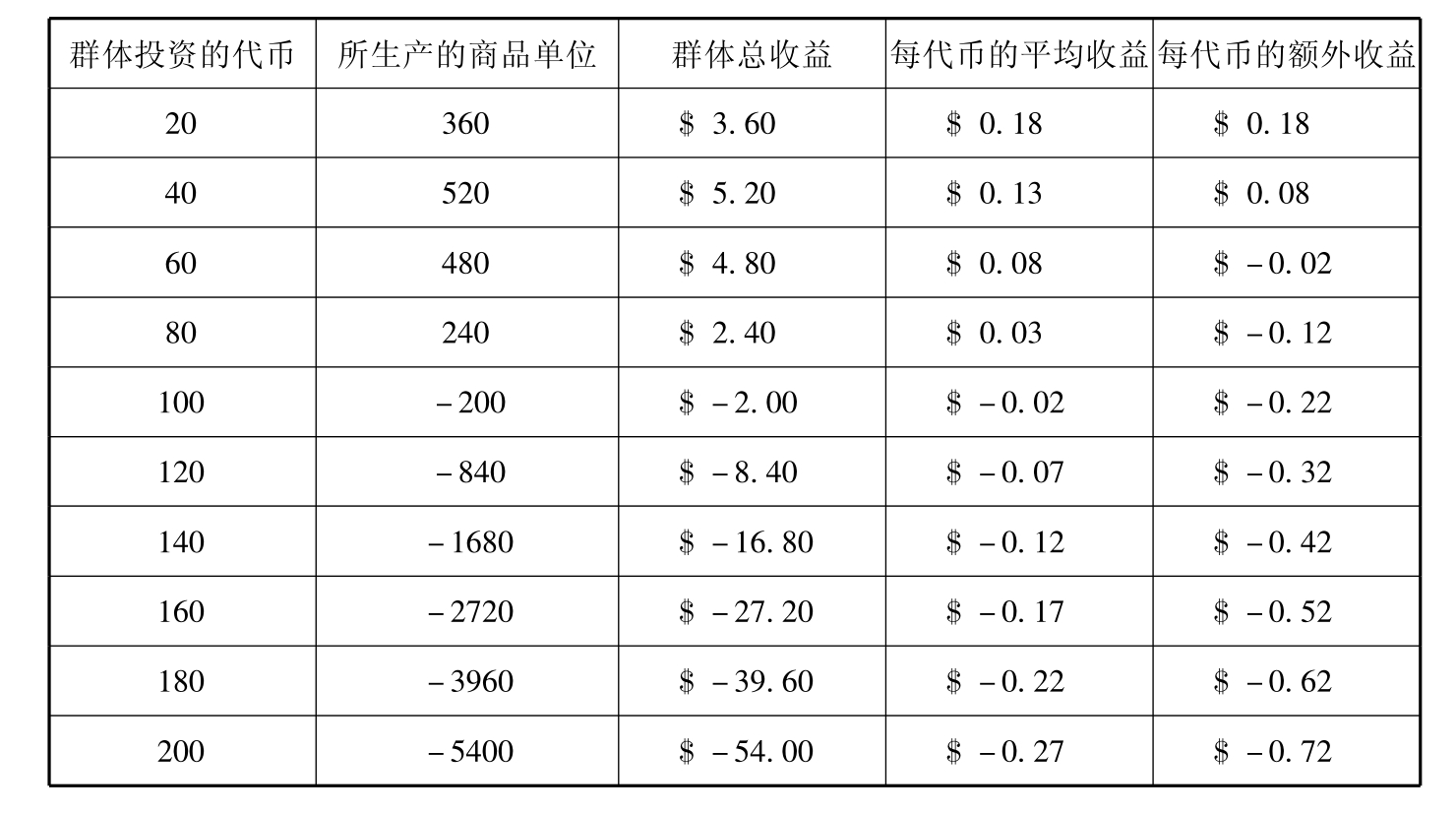
注:此表所列信息是各群体投资的市场2的投资状况。从市场2得到的收益取决于投资人在群体总投资中的百分率。

给市场1每投资1个代币，市场1返还1个单位的商品1。每单位商品1的收益是$0.05。

图5.1　出示给实验被试的图。该图显示了在市场2中投资的生产与现金收益状况。

(每单位商品2的价值为$0.01)

在基线实验中，8个被试参与了一系列至少有20轮决策的实验。每轮过后，我们都会向被试出示记录内容:(1)他们在本轮从两个市场中所获得的利润;(2)市场2中的群体总投资;(3)他们在实验过程中累积的利润。在实验期间，被试可通过计算机询问所有有关以往轮次的信息。但局中人不会获得有关其他人的个人投资决策，或投资将会重复的次数等相关信息。

需要指出的是，这个实验室的决策情境与第二章描述的行动情境是相应的。周密的实验考察要求对行动情境七个要素的每一个都加以明确界定。因此，我们在实验室所设计的基线行动情境包括下列行动情境要素:(1)8个参与者;(2)所有参与者拥有同样的位置;(3)参与者必须为受实验控制的各个决策轮作出代币分配;(4)市场1与市场2的产出用生产单位表示;(5)以明确的函数把市场1与2的总投资对应于市场1与市场2的生产单位数目;(6)参与者了解其他局中人的数目、他们各自的禀赋以及各自过去的行动、所有其他人的群体行动、两个市场产出的单位收益、分享市场2产出的分配规则、博弈的有限重复性;(7)参与者知道投资决策与净收益的映射关系。

下面，我们来解释一下基线实验室公共池塘资源的情境。由于参与者的上限为8个局中人，对公共池塘资源(市场2)的投资上限为这8个人所拥有的代币总量，就此意义而言，这属于有限进入。尽管这个决策情境的局中人有限，但是组合在一起的局中人有充分的自由选择可导致极端次优收益的投资水平。事实上，我们考察的是提取者每轮每人的原始资本(被给予的代币数)从10变到25时所带来的行为后果。虽然8个局中人不算多，但是由于基线设计不允许公开交流，因此，这种情境的群体具有较大群体或者冲突四伏的小群体的一些特征。在这个基线实验中，人们很难相互传递自己的意图。个人行动的信息会淹没于其他人的行动中，因为局中人只能获得有关群体投资决策与结果的信息。

而且，我们的实验室公共池塘资源在比较短的时间内把事先互不相识从而不可能暗地协调行为的局中人聚集在一起。参与者明白该实验不会超过两个小时，而且所有的决策对其他参与者都将是保密的。^[4]因此，虽然参与者不知道具体的轮数，但他们知道实验时间比较短且有限。实验情境被有意识地中立化，因为局中人不能公开获知有关下列内容的线索:(1)我们对他们的期望;(2)在自然条件中对应发生的决策环境(例如，我们并不以渔民称呼他们或把市场2称为渔场)。最后，再次强调的是，实验的基线情境将提取活动与提供活动分隔开了。资源由实验者提供。被试所做的决策，不会对他们最初被给予的代币数、生产函数、收益函数与决策轮数有任何影响。

2.对基线实验中个人行为的理论预测

假设有固定数量的n个提取者进入公共池塘资源。每个提取者i拥有资源禀赋e，并可把e投资到公共池塘资源或者投资到安全的外部活动。外部活动的边际收益统一定为w，以美分来衡量。投资公共池塘资源的提取者的收益，取决于群体对公共池塘资源的总投资与提取者投资在总投资中所占的比率。设x_i代表提取者i对公共池塘资源的投资，其中0≤x_i≤e。公共池塘资源投资的群体收益由生产函数F(∑x_i)给定，F是凹函数，且F(0)=0，F’(0)＞w，F’(ne)＜0。起初，对公共池塘资源的投资收益比安全投资的机会成本更高［F’(0)＞w］，但如果提取者投资于公共池塘资源的资源量(q)足够大，那么结果就会是“血本无归”，即［F’(q)＜0］。当个人只把部分(而非全部)的资源禀赋投资于公共池塘资源时，从公共池塘资源得到的收益会达到最高净水平。^[5]

到现在为止，我们所考察的全部公共池塘资源博弈都只有两个局中人。这种限制只是为便于说明问题。现实中的多数公共池塘资源问题所包括的参与者数目比这要多得多。我们设参数n为公共池塘资源实验博弈的局中人数目。本书所统计的全部实验都设n=8。尽管许多公共池塘资源问题涉及的参与者超过8个，但8个参与者足以将大群体博弈固有的绝大多数复杂的策略问题呈现在我们面前。同时，有合理的理论依据可以相信，8这个数量也足以克服小群体效应。^[6]

现在介绍一些有用的符号。设x=(x₁…x_n)为个体提取者公共池塘资源的投资向量。个人i没有对公共池塘资源提取的量是e－x_i，它被自动投资于安全的外部活动。向量符号x提醒我们注意，参与者的收益取决于所有参与者所做的选择。因此，每位提取者的收益u_i(x):

如果x_i=0，则u_i(x)=we

如果x_i＞0，则u_i(x)=w(e－x_i)+(x_i/∑x_i)F(∑x_I)　　　　(5.1)

方程式(5.1)所说明的内容非常直观。如果局中人把所有的资源禀赋都投入到安全活动中，他们的收益就会是一个定值(即资源禀赋×每单位禀赋的收益值=ew)。如果局中人把部分资源禀赋投资于其他安全活动，而把其他投资于公共池塘资源，他们从安全活动投资所获得的收益为w(e－x_i)。除此之外，他们从公共池塘资源得到的收益，与其投资在公共池塘资源中的总投资成正比(x_i/∑x_i)，我们以美分作单位。

博弈的局中人越多，博弈就越复杂。然而，收益最大化与纳什均衡这些基本概念是不变的。尤其在纳什均衡上，每个局中人都在对方的策略选择限定的条件下，实现了收益的最大化。设x_i是局中人i的策略，u_i(x)是局中人i的收益函数，且其中的变量关系符合方程式(5.1)。局中人i寻求通过选择x_i最大化自己的收益，而x_i本身就是受约束的变量。当收益函数像(5.1)中表示的情况一样时，我们可以应用微积分运算实现这种最大化。我们来看看下面的微积分问题:

u_i(x)最大化

　 x_i

满足0≤x_i≤e

设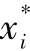解决了这个有约束条件的最大化问题，且u_i(x₁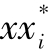，…，…x_n)是最大值。这样就形成了一个n元方程。现在我们来求解每个局中人i的微分问题。由于有n个局中人，因此我们会得到n个方程。而这个方程组的解就是纳什均衡。换句话说，纳什均衡要求所有n个局中人已同时解出自己的个人收益最大化的问题。即，假设对每个局中人i而言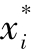，是个人最大化的解。那么，在纳什均衡中，局中人i所面临的问题(如果其他每个局中人都在追求最大化——即最优选择的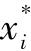)的解是。

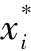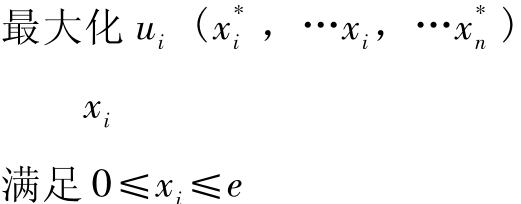
由于每个局中人都有一阶条件，因此，一般求解纳什均衡需要解决n元函数的n个同组方程。从计算上讲，解这个方程组的难度非常大，这也是为什么有多个局中人的博弈较难分析的原因。

然而，如果博弈是对称的，就可以找到求解的捷径。我们的基线博弈是对称的。每个局中人有相同的资源禀赋、相同的纯粹策略集合(并因此有相同的混合策略)、与相同的以美分为单位的收益函数。在这些条件下，博弈是对称的。每个对称博弈有一个对称的均衡。如果对称博弈有唯一的一个对称均衡，那么我们可以依据豪尔沙尼—泽尔腾的选择理论找到这个均衡。^[7]要找到这个对称均衡，只要在其所要求的约束条件——均衡上每个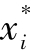都相等时，求出一个局中人的最大化问题的解就可以了。

我们以收益函数(5.1)来说明这种方法。根据我们对公共池塘资源生产技术预先假定的情况，我们很容易知道，x_i=0与x_i=e都不能解决局中人i的最大化问题。因此，必定存在一个内在解可以满足一阶条件。对(5.1)函数求导，有:

所谓对称，即在均衡上，每个局中人的投资决策与局中人i相同。要有对称，必有∑x_i=n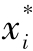。代入方程(5.2)得出

下文将证明，对称纳什均衡的公共池塘资源总投资大于最优投资，且群体利润小于最优回报，但是并没有损耗全部公共池塘资源的收益。^[8]

对这种对称纳什均衡，有以下几种标准解释。第一，这是面临最大化问题的理性局中人的唯一解。第二，如果局中人不遵从(5.2)，他们的收益将是次优的。第三，一旦局中人达到这种均衡，他们就不再有改变自己行为的激励。第四，若人们相信策略行为可以随时间进行调整，那么演化的力量(模拟自然选择)最终将导致令人满意的均衡(5.2)。^[9]最后一个解释是，这是对有限进入的公共池塘资源的预测结果(参见Clark 1980;Cornes and Sandler 1986; Hartwick 1982;and Negri 1989)。^[10]这个解释对政策目标关系最为密切。

我们现在将该均衡与公共池塘问题的最优解做个比较。加总所有提取者i的个人收益u_i(x)，即得到群体收益函数u(x)，

u(x)=nwe－w∑x_i+F(∑x_i)　　　　　(5.3)

这个函数要在约束条件0≤∑x_i≤ne下最大化。若F的生产力条件如前所定，那么群体最大化问题拥有唯一解的条件是:

－w+F’(∑x_i)=0　　　　　　　　(5.4)

按照(5.4)，投入到公共池塘资源的最后一个投资单位，其从公共池塘资源获得的边际收益应等于外部替代活动的机会成本。当边际收益等于边际成本(5.4)时，群体收益就为一个周期内可以从公共池塘资源中获取的最大值。由于方程(5.4)与(5.2)有不同的解，因此可以说明，均衡并不是最优。^[11]

只要资源禀赋参数足够大，纳什均衡投资与最优群体投资都不由e决定。对于纳什均衡而言，这个结论看起来特别违反直觉预测，因为e值大，说明对公共池塘资源的潜在压力很高。从策略上看，公共池塘资源困境最难处理的一个问题是由高禀赋所引起的过度提取。资源禀赋数额越大，大错误出现的概率也就越高，其破坏性也就越大。如果投资不能超过禀赋这个条件不再具有约束性，那么纳什均衡概念就不再能解决这个问题了。^[12]

我们以X表示基线博弈，设X进行有限次数。理论博弈模型并不一定总是能就个人在重复性社会困境情境将(或应当)如何行为的问题产生唯一的解。即便一次性博弈拥有唯一的均衡，此类有限重复基线博弈也能有多个均衡。均衡数随着重复次数而增加。当重复的次数为有限多时，任何均衡都不可能达到最优，但它有可能接近最优(见Benoit and Krishna 1985)。当重复的次数为无限多时，某些均衡可以实现最优解(见J.Friedman 1990)。无论在何种情况下，最不可能的一次性均衡，只要博弈重复的次数足够频繁，也会变成均衡结果。因此，局中人面临着均衡过多的情境。若不建立均衡选择机制，局中人就很容易陷在复杂与混乱中而无所适从。

通用的均衡选择标准是，该策略必须能够实现各个子博弈均衡，即子博弈完美要求。如果基线博弈有唯一的对称均衡，那么有限重复博弈就有唯一的对称子博弈完美均衡(见Selten 1971)。所以，(5.2)方程式表明了有限序列的均衡结果。在这个方程中，无论是在同一决策期还是在不同决策期，局中人之间都是对称的。

与我们在本章中所做的其他所有预测一样，这个预测成立的基础是有限博弈论与完全信息假设。我们的实验程序确保被试知道博弈是有限的。^[13]尽管我们并不完全了解被试是如何理解自己的决策任务的，但是实验所提供的信息满足完全信息的要求。我们一方面只使用经历过基线实验的被试来进行实验，另一方面，我们会向他们提供实验结果。再加上实验指示与问答环节的安排，我们确信实验被试真正理解了他们所面对的实验室情境。如果说他们有不理解的地方，那就是如何在包含着子博弈完美均衡的多个博弈均衡中作出选择(见Kreps et al.1982)。

3.实验设计

在实验研究中，公共池塘资源情境设置为:8个提取者(n=8)与二次生产函数F(∑x_i)，其中:

F(∑x_i)=a∑x_i－b(∑x_i)²(www.daowen.com)

满足F’(0)=a＞w和F’(ne)=a－2bne＜0　　　　　　(5.5)

对于这个二次方程，我们可以根据(5.4)推出，群体最优投资满足∑x_i=(a－w)/2b。当投资是最优的两倍，即∑x_i=(a－w)/b时，公共池塘资源净收益为0%。最后，从(5.2)可以推出对称纳什均衡上的群体投资是:

∑x_i=［n/(n+1)］(a－w)/b　　　　　　(5.6)

这个投资水平介于最大净收益与零净收益之间，n越大，投资水平越接近零净收益。实验室场景下的一个额外约束条件是:x_i为整数。这是通过设定参数a，b，n和w的取值使与∑x_i相关的推断均为整数值来实现的。

下面，我们来考察利用表5.1所列参数进行的实验。图5.2给出这些参数所形成的预测。其中36个代币的群体投资产生了最优投资水平。这个对称博弈有唯一的对称均衡，即每个对象对市场2投资8个代币。

表5.1　基线实验设计中，给定决策轮所用的参数

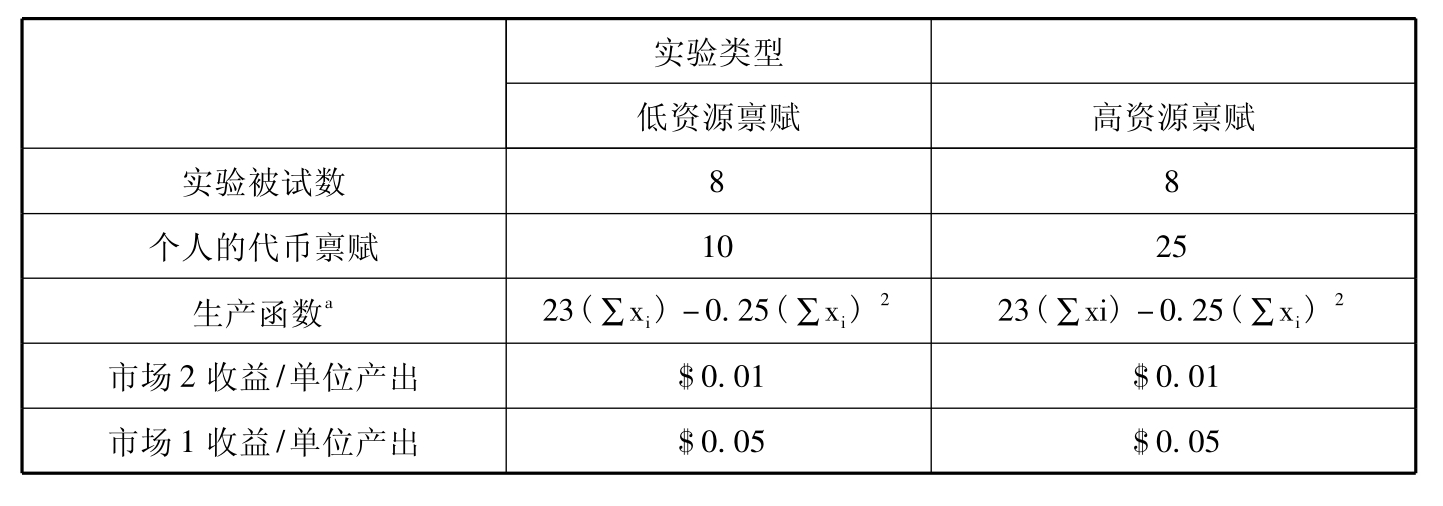
续表

a生产函数显示出投资到市场2的每水平代币在市场2的单位产出数。∑x_i等于群体投资到市场2的代币总数。

b表中所表明的数目是可能的现金收益。在高资源禀赋实验设计中，被试获得的现金等于他们在计算机上决策所赚的钱的一半。

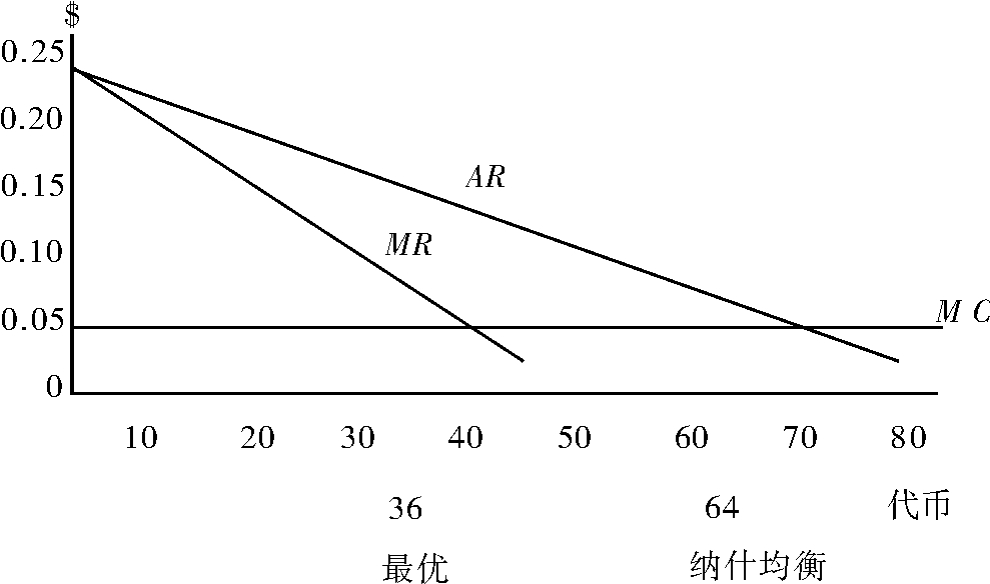
5.2　理论预测(MR=边际收入，AR=平均收入，MC=边际成本)

我们有关实验结果的探讨，重点是为了说明公共池塘资源的最大净收益。它可以帮助我们衡量从公共池塘资源取得的收益的最优化程度。具体来讲，净收益是市场2中所获收益减去代币投资到市场2的机会成本，除以当边际收益等于边际成本减去代币投向市场2的机会成本时的市场2的收益。^[14]在我们的决策情境下，机会成本等于代币投向市场1有可能获取的收益。^[15]注意在公共池塘投资水平一定的情况下，相对于被试的资源禀赋而言，净收益是恒定的。须知即使实验被试投资决策的范围随着被试资源禀赋的增加而增加，但是均衡与最优投资并不变。在纳什均衡上，被试所获得的净收益大约为公共池塘资源可产生的最大净收益的39%。

4.实验结果

表5.2与图5.3总结了六个实验，其中三个是10代币禀赋实验［实验1—3］、另外三个是25代币禀赋实验［实验4—6］)的基线结果。^[16]附录5.3按轮次列出了所有六个基线实验的市场2投资决策。表5.2列出了实验被试群体实际赢取的净收益。最引人注意的是，代币禀赋从10增长到25以后的现象。总计所有的实验决策轮，得出低资源禀赋(10代币)时获得的平均收益等于37%。比较而言，高资源禀赋(25个代币)获得的平均收益为－3%。我们可以从表5.2看出，在早期实验轮里，高资源禀赋发挥了重要作用。其中，大量的实验被试对市场2进行高投资，导致净收益处于低最优382%的低水平。随着实验的进展，次优程度逐渐接近低资源禀赋条件下的次优水平。如图5.4六个实验中前20个决策轮的平均趋向。

单个实验有几个非常重要的特征。我们以“脉冲”模式形象地描绘对市场2的投资，其中，投资增加导致收益下降，此时投资者往往会减少对市场2的投资，于是收益增加。在实验中，这个模式一般会随着决策轮而重复发生。然而，我们发现，高峰振幅或时间内并没有出现实验对称。对于高资源禀赋实验，脉冲低点上的收益远低于0。在实验过程中，收益变化呈一定的下降趋势。我们没有发现可以说明实验稳定的明显信号。而且，我们没有看到在哪个实验中，个人对市场2的投资稳定在一次性纳什均衡上。^[17]我们将在下面四章解释这种行为的结果，即个体情况不符合纳什均衡。^[18]

我们获取的资料在多大程度上符合对这种情境下的个体均衡预测?要解答这个问题，需要首先研究两个基本的学术问题与一些更具体的问题。

问题1——各轮次观察到的结果在多大程度上满足向市场2分配64代币的标准?

问题2——个人作出8代币投资的轮次频率是多少?

下面我们总结一下整个实验中上述现象的出现频率，以说明个人决策在多大程度上符合方程式(5.2)的预测，即对公共池塘资源投资8代币。我们把这两个问题分解成子问题。每个子问题后面括号内的数字是在10代币实验(以及25代币实验中)与每个问题相对应的观察结果的百分比。

问题1——各轮次观察到的结果在多大程度上符合向市场2分配64代币的标准?

(a)有64代币被分配给市场2的轮数(11%，5%)。

(b)有64代币投入市场2，所有对象都投资8代币的轮数(0%，0%)。

问题2——个人作出8代币投资的轮次频率是多少?

(a)所有投资都为8的轮次(0%，0%)。

(b)除一人外，其他所有人的投资都为8的轮次(0%，0%)。

(c)除二人外，其他所有人的投资都为8的轮次(0%，0%)。

(d)除三人外，其他所有人的投资都为8的轮次(0%，0%)。

(e)除四人外，其他所有人的投资都为8的轮次(1%，0%)。

(f)除五人外，其他所有人的投资都为8的轮次(6%，3%)。

(g)除六人外，其他所有人的投资都为8的轮次(23%，7%)。

(h)除七人外，其他所有人的投资都为8的轮次(37%，37%)。

(i)都不投资8代币的轮次(32%，48%)。

简言之，观察结果几乎没有支持这样的学术假设，即我们的投资环境将稳定在一次性纳什均衡之中。在10代币条件下设计的90轮实验中，我们发现仅有10轮，其市场2的总投资是64。而这10轮中没有1轮出现过每个被试都投资8代币的情况。而且，在所有90轮的投资中，我们发现了8个被试中最多有4人投资纳什均衡预测的8代币的情况。相比之下，25代币禀赋条件下设计的实验更不支持个体层次的纳什均衡预测。60轮投资中仅有3轮市场2的投资等于64，且这3轮中不存在所有8位投资者都投资8代币的情况。另外，在全部的60轮中，我们发现投资纳什均衡预测8代币的最多时只有5人。

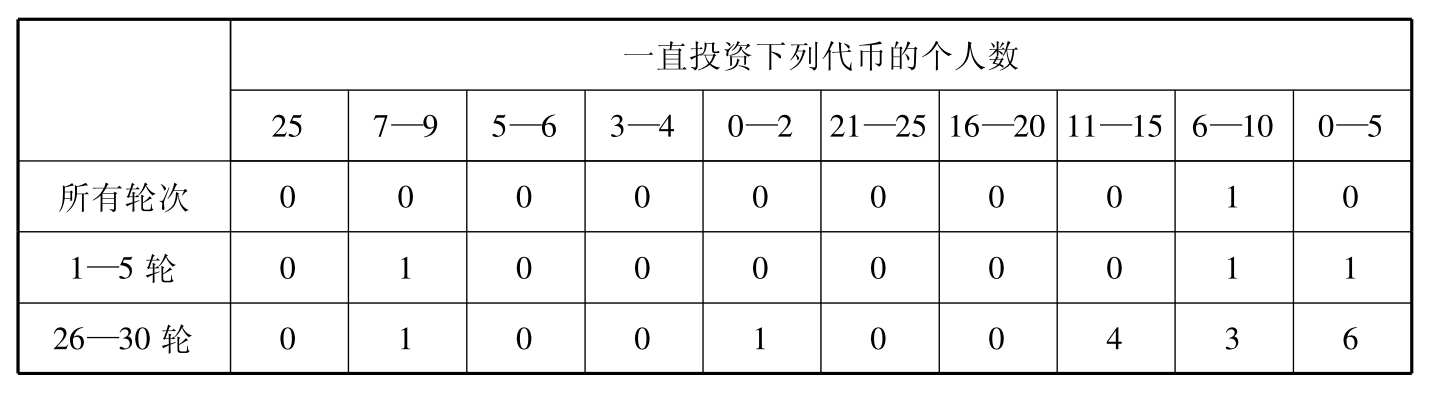
再看表5.3与表5.4，我们来集中研究各轮的个人策略。3个10代币实验的24个被试中，没有一个人坚持实行在市场2投资8代币的策略。而且，我们发现，没有被试连贯一致地在与纳什均衡相差1的范围内进行投资(投资9、8或者7)。如果我们只分析30轮实验的最后5轮，会有什么情况发生呢?在这最后5轮中，有3个人连贯一致地围绕纳什均衡预测数值相差1代币的范围内进行实验。我们也发现，24个人中，有19人在市场2的投资区间更广泛，从6到10个代币不等。然而，与我们以前的设计一致的是，我们发现了一个很强的模式，即局中人在市场2投资全部10个代币。实际上，在最后5轮中，24个局中人中有6人一直投资10个代币。表5.4提供的是25代币实验的有关信息，其个人行为的信息与表5.3提供的颇为类似。我们发现，25代币实验的观察结果几乎也不支持个体层次上的纳什均衡预测。而且，25代币设计实验明显改变了我们在10代币实验中所发现的分配约束。没有局中人一直坚持投资25个代币。

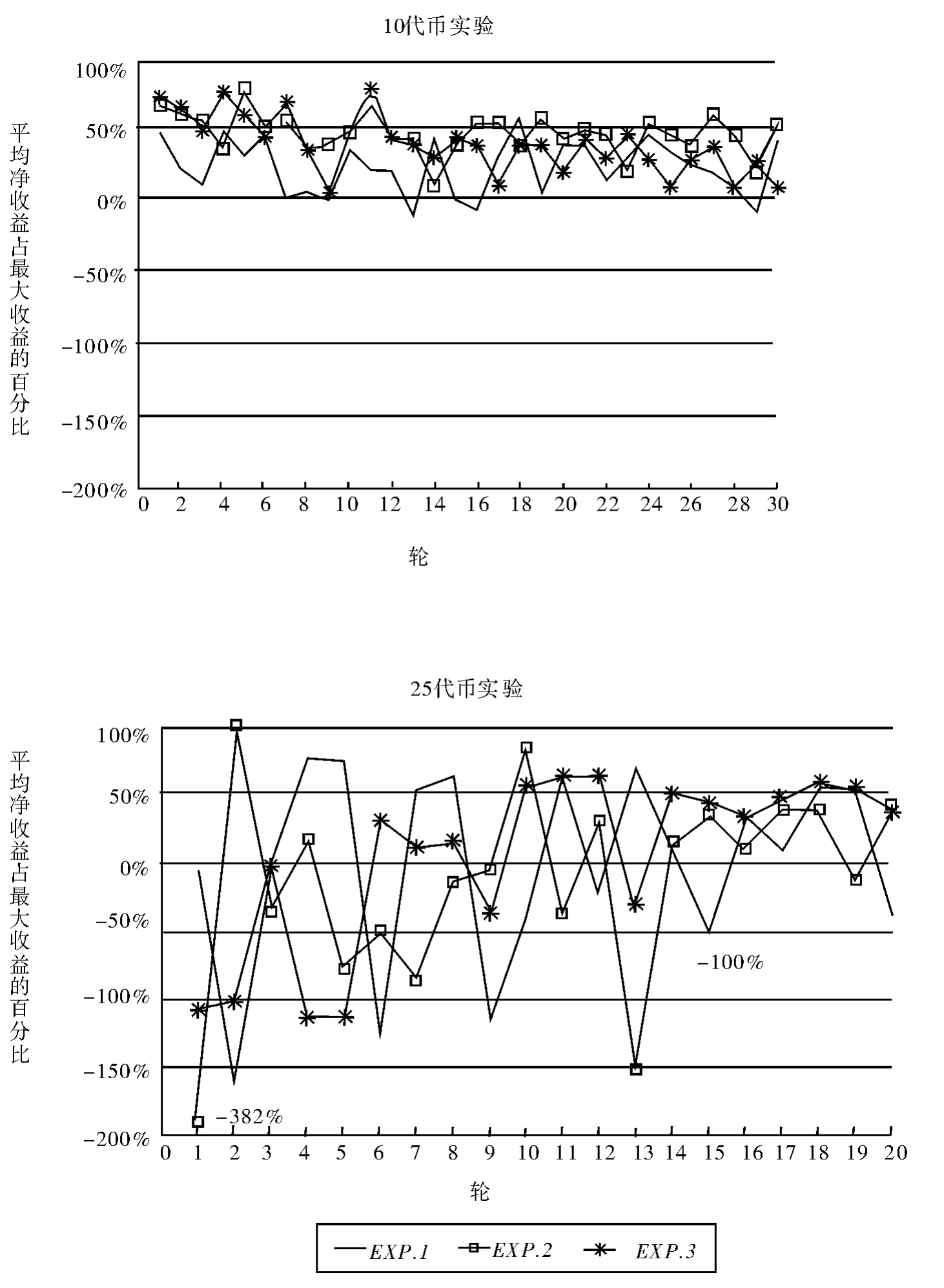
图5.3　个人基线实验

表5.2　基线实验设计中平均净收益占最大收益的百分比

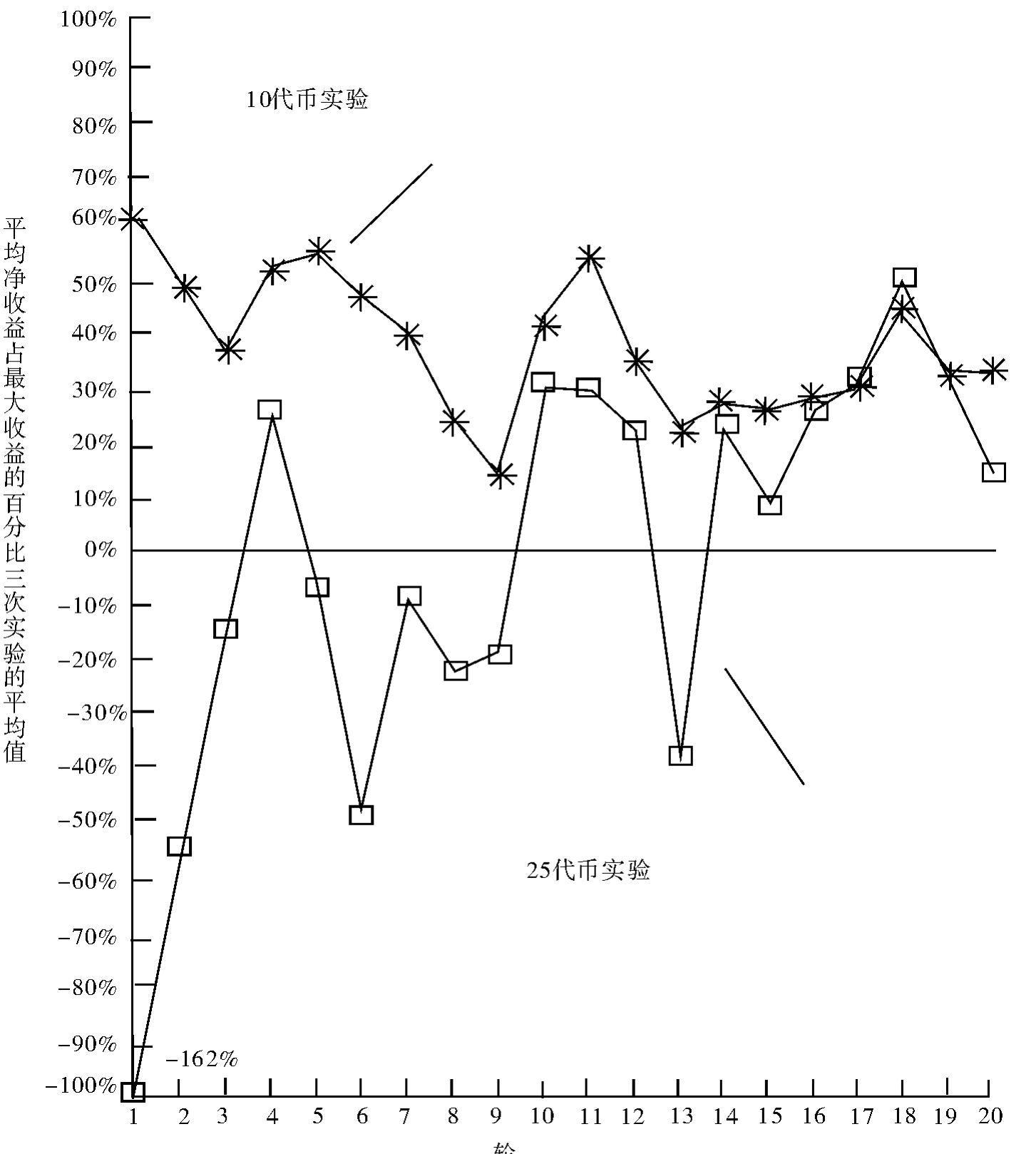
图5.4　投资禀赋增长带来的影响

表5.3　10代币实验的个人投资模式

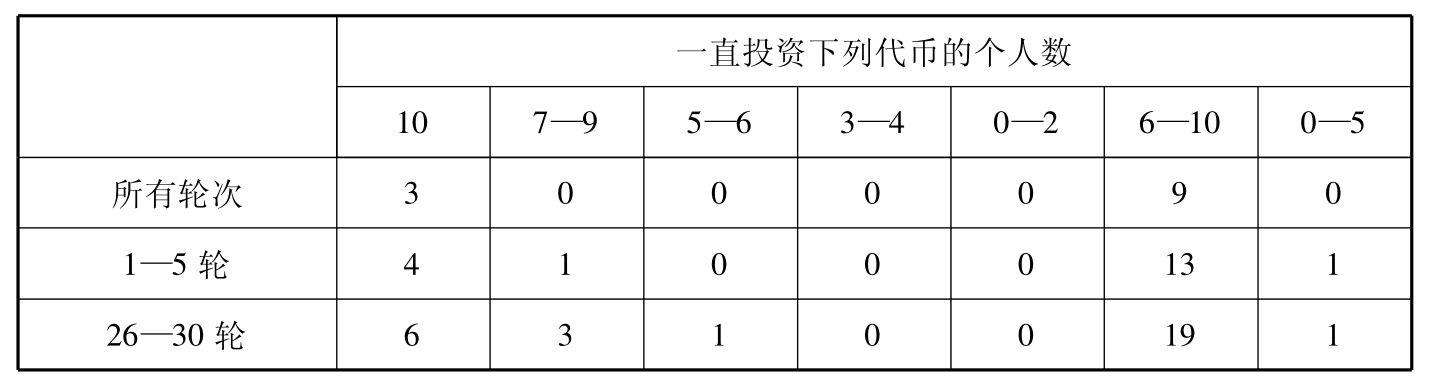
表5.4　25代币实验的个人投资模式