第三节 捕鱼规则与捕鱼博弈
1.概述
通过上文的简要描述,我们可以看出在实践中把价值各异的地点分配给渔民的规则具有多样性。[14]但如果缺乏获得一致认同的规则来对捕鱼地点的使用权进行清晰的分配——正如第一个发生在西马来西亚的例子,则很可能会导致冲突与暴力。很多时候,就清晰分配权利制定各种具体的权威规则的可能性是存在的。人们使用的每类规则(在与物理学与生物学规律的共同作用下)对博弈结构的影响,可能(也可能不)足以产生不同的均衡与不同的福利分配。
为了说明与自然领域相结合的规则如何影响着博弈的结构与相应的均衡,我们来分析四种简化的具有代表性的规则体系。首先,除权威规则与位置规则外,其他所有的规则都设为缺省状态。也就是说,规则允许渔民独立行动、其行为对结果的影响只受自然因素的限制,并且可以保留自己捕获的鱼而无须考虑外部的报酬或承担外部的成本。这样做可以使我们集中关注:在边界规则或收益规则与特定的权威规则之间不存在互动的情况下,权威规则的变化会给渔民对捕鱼地点的使用权造成什么样的影响。[15]
正如我们在第一章与第三章已讨论过的,当公共池塘资源使用者为各种空间或各个时间期限而相互竞争时,分配问题就产生了。问题并不在于资源正在被过度开采或者资源处于毁灭的边缘,而在于一些捕鱼点好于其他捕鱼点,冲突围绕着谁能在较好的点上捕鱼而爆发。包括重大国际国内冲突与战争在内的很多情境,都存在分配问题。我们这里所研究的分配问题,都是由前一章所研究的基础性分配问题推演而来。
捕鱼分配博弈是特定自然参数与规则体系共同作用的结果。自然参数包括渔民数量、不同点的数目与在点与点之间转移的成本。在我们改变规则以考察规则对博弈的影响效果时,上述参数设为常量。四种被简化的代表性规则体系,只在权威规则与位置规则方面有区别(见表4.1)。在此表中,纵列中的数值1代表对应的规则存在,0表示该项规则不存在。规则体系C1有两个位置:局中人1(处于较强位置)与局中人2(处于较弱位置)。与较弱位置的局中人相比,处于较强位置的局中人更有可能赢得对捕鱼点的争斗。C1描述了霍布斯式的捕鱼状态。规则体系C2有“先到者、权利优先”的权威规则。两个位置是局中人1(首先占领的可能性较大)与局中人2(首先占领的可能性较小)。C 2不存在争斗问题。规则体系C3拥有“先宣告者,权利优先”规则。两个位置是局中人1(首先宣告)与局中人2(听到宣告)。规则体系C4是一个就捕鱼点、单个位置与渔民预先安排好的轮流制度。
表4.1 规则体系
2.形式博弈
根据前面的条件设定,现在有渔民1与渔民2,两个捕鱼点:记为点1与点2。每个捕鱼点i的价值按照所能捕获的鱼量vi来衡量,点1比点2好,即
v1>v2 (4.1)
对两个渔民来说,两个捕鱼点的价值为恒定量。渔民从一个捕鱼点转移到另一个点的成本是c,而c小于较差点的价值,即
v2>c (4.2)
最后,每一个渔民可能给另一个渔民造成损失量,记为d。根据博弈的具体情况不同,损失情况可从微弱(破坏捕鱼器)上升至严重(伤害人与船)。自然矢量参数(v1、v2、c、d)适用于所有规则体系。自然参数的变化将导致新的自然领域的产生。
除了四个自然参数外,还有一个重要的行为参数。因为一个捕鱼点好于另一个,所以当两个渔民都提取同一个捕鱼点,而权威规则又不能解决问题时,可能会发生争斗。假设渔民1与渔民2之间就捕鱼点发生争斗。渔民1赢得争斗的概率为P;渔民2赢的概率就为1-P。因为渔民1强于渔民2,所以有:
P>0.5 (4.3)
发生争斗的唯一规则体系是C1;这是行为参数P将影响自然领域的博弈。
规则体系C1
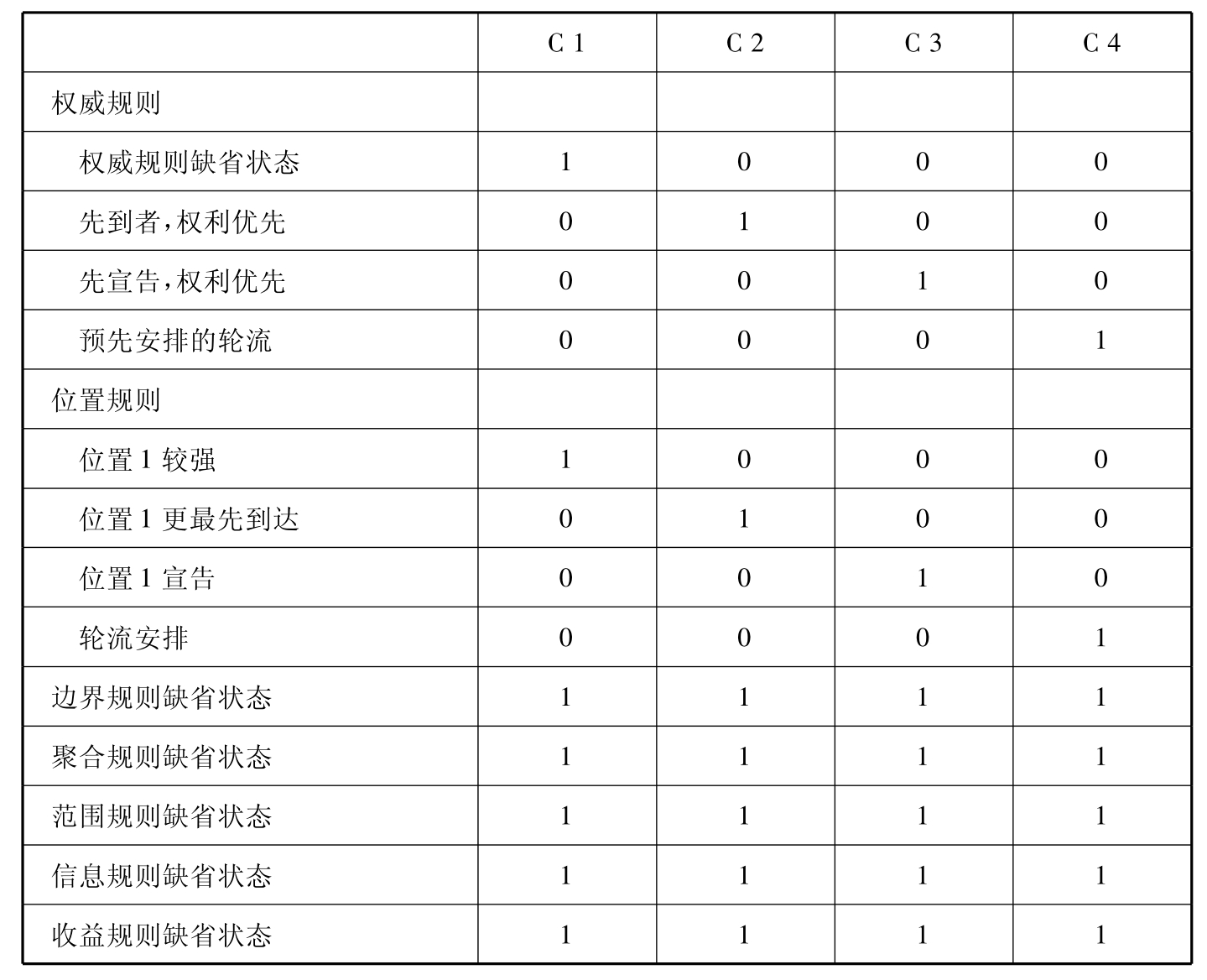
我们现在分析遵循规则体系C1的博弈。该博弈始于每个渔民对捕鱼点的选择。两人的选择同时进行,但又都是独立作出决策。倘若两个渔民去了不同的捕鱼点,则博弈结束,两人各获得自己所选的点的价值。倘若两个渔民去了相同的捕鱼点,博弈继续进行。图4.2Ⅰ显示了这个博弈。(点1,点1)的结果,即“去G1”,指博弈将以博弈G1的情境下继续进行;同样,如果两人作出的选择是(点2,点2),那么博弈在此点上将以博弈G2的情境下继续进行。
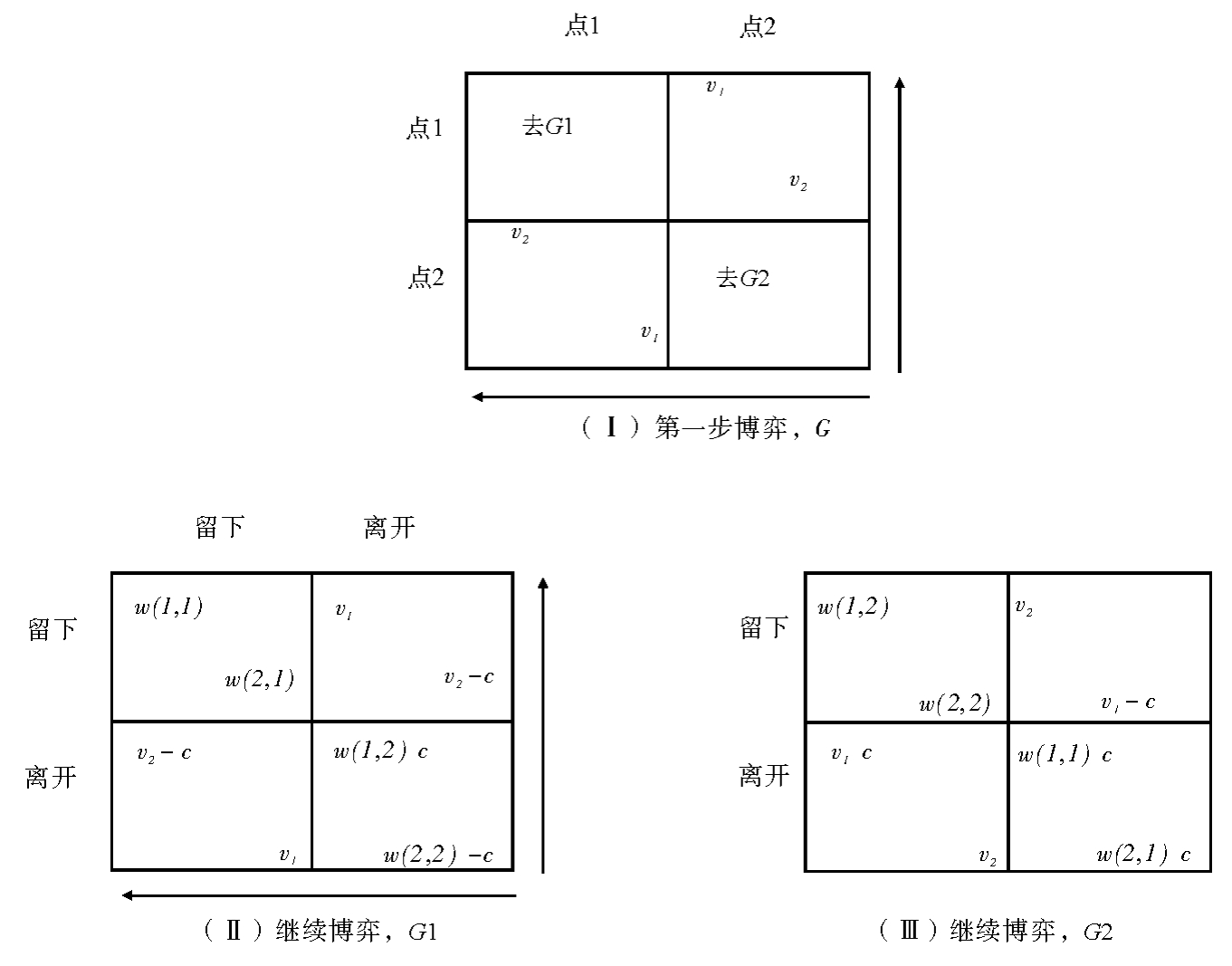
图4.2 根据规则体系C1建构的博弈
继续博弈G1与G2可能涉及争斗。在这两个博弈中,每个渔民都要在留在点上与移至另一点之间作出选择。一旦渔民发现两人处于相同点上,接下来可能会有四种情况发生。如果其中一个渔民移往另一个点,而另一个人留在原地,那么离开的人的收益为另一个点的价值减去移动成本c(根据谁离开与谁留下,这里有两种情况)。若两个人都留下,且争斗即刻发生,此时,在概率P发生的情况下,渔民1赢得争斗,且该点的价值没有损失;在概率是1-P发生的情况下,渔民1在此点上被打败,遭受损失(收益为-d),并且丧失一起捕鱼的机会。以w(1,i)表示渔民1在点i上即刻争斗的收益值。综上所述,我们可以得出
w(1,i)=Pvi+(1-P)(-d)
同样,w(2,i)表示渔民2在同一点上进行争斗所得到的价值。两种概率正好相反,可得
w(2,i)=(1-P)vi+P(-d)
由于P>0.5,因此,可以推出,对于任何点i,都有w(1,i)>w(2,i)。最后,两个渔民都可以离开他们所去的点,而前往另一个点。此时,他们发现自己又处在同样的点上,新点上的争斗又即刻发生。以j表示新点,那么他们的收益分别是w(1,j)-c与w(2,j)–c,即两人在点j争斗后的所得减去到达新点的移动成本。图4.2Ⅱ与4.2Ⅲ反映的是两个渔民都去点1后的继续博弈G1与两个渔民都去点2后的继续博弈G2。
为分析规则体系C1规治下的博弈局,我们先从研究继续博弈G1与G2开始。这样,我们就可以找出“去G1”与“去G2”对收益关系的影响,并由此求出博弈G的解。这种自博弈终端开始求解复杂博弈的过程被称作倒推。以继续博弈作为子博弈,我们可以利用倒推来建构子博弈完美均衡。
开始倒推之前,首先考察子博弈G2。为了给图4.2Ⅰ的箭头图表标明箭头,我们只寻找有关G2的足够信息。先考察子博弈G2的局中人1。这个局中人的收益可能是w(1,2),v1-c,v2,w(1,1)-c,或者是这些值的特定概率的混合。注意,当局中人2在点2时,局中人1直接去点1而不是点2所获得的收益v1大于上述任何一种情况能够获得的收益。因此,博弈G局中人1的箭头背离点2,指向点1。如图4.2Ⅰ所示。这样的考虑也同样适用于子博弈G2中的局中人2,与局中人1相比,局中人2在子博弈G2中可能的收益不仅不可能高过前者,甚至还可能更低。由此可见,无论子博弈G2中会发生什么,在均衡状态下,两个局中人的第一步都不会选择去点2。如图4.2Ⅰ博弈G的箭头所示。
对子博弈G1的分析会更复杂些,因为需要考察多种情况。这样做是有根据的。假如可以为好的点而争斗,选择为差的点争斗显然讲不通。这种考虑反映在不等式v1>w(2,2)-c与v1>w(1,2)–c上,因此,G1的箭头都是背离点(离开,离开的)。G1有三个可能的箭头图表。第一个箭头图表可能带来(C1-1,C1-2,C1-3)三种情况中的一种。第二个箭头图表将导致C1-4的情况,第三个图表的结果是C1-5。对于每种情况,我们都会直接倒推至整个博弈G并对其进行求解。
在继续博弈G1的第一个可能的箭头图表(图4.3Ⅰ)中,局中人2顶端的箭头指左,局中人1左边的箭头指上。每个局中人都愿意离开只有自己孤身一人的点2,去点1与另一人发生争斗。这种情况的发生需要以下面两个不等式的成立为前提条件:
w(1,1)>v2-c
w(2,1)>v2-c (4.4)
如箭头图表4.3Ⅰ所示,每个局中人在子博弈G1的支配策略都是留下。这意味着G1的结果如果可以实现的话,是[w(1,1),w(2,1)]——即每个人都留在点1并为之争斗。我们现在来考虑C1-1、C1-2与C1-3三种不同情况下的G博弈矩阵(分别是图4.3Ⅱ、图4.3Ⅲ、图4.3Ⅳ)。记住,所有这些箭头图表以图4.3a所描述的G1中的行动与不等式(4.4)为依据。
情况C1-1。首先考察图4.3b给出的G箭头图表。在这个图表中,局中人2顶端的箭头指左,局中人1左边的箭头指上。这种情况下G的均衡是(点1,点1)。两个渔民都去点1,并选择留下来进行争斗。这里要求下面两个不等式成立
w(1,1)>v2
w(2,1)>v2 (4.5)
例如,在两个局中人的力量在伯仲之间(P接近0.5),且点1比点2好得多(v1>>v2)时,这种情况就会发生。
情况C1-2。现在考察图4.3Ⅲ给出的G箭头图表。在这个图表中,局中人2顶端的箭头指右,局中人1左边的箭头指上。这种情况下G的均衡是(点1,点2)。力量较强的渔民去较好的点。这里要求的前提条件是
w(1,1)>v2
w(2,1)<v2 (4.6)
例如,当两个局中人的力量对比悬殊(P接近1)时,这种情况就会发生。
情况C1-3。考察图4.3Ⅳ给出的G箭头图表。在这个图表中,局中人2顶端的箭头指右,局中人1左边的箭头指下。这里对应的不等式是
w(1,1)<v2
w(2,1)<v2 (4.7)
当两个局中人在力量上难分高下(P接近0.5)且两个点的价值几乎相等时,这种情况就可能发生。博弈G此时属于胆小鬼博弈的例子,拥有多个均衡。根据我们前面的讨论,每个胆小鬼博弈都有三个均衡。“强者即正义”这个格言就适用于其中的一个均衡(点1,点2)。较强的局中人得到较好的点。另一个纯策略均衡(点2,点1)有点悖论的意味,格言在此变成了“弱者即正义”。最后,由于博弈是不对称的,因此,混合策略均衡(这种均衡能使两人的收益更均等)出现的可能性比在博弈为对称的情况下少。所以,我们选择均衡(点1,点2)作为G的结果。[16]
注:代表均衡
图4.3 C1-1、C1-2、C1-3
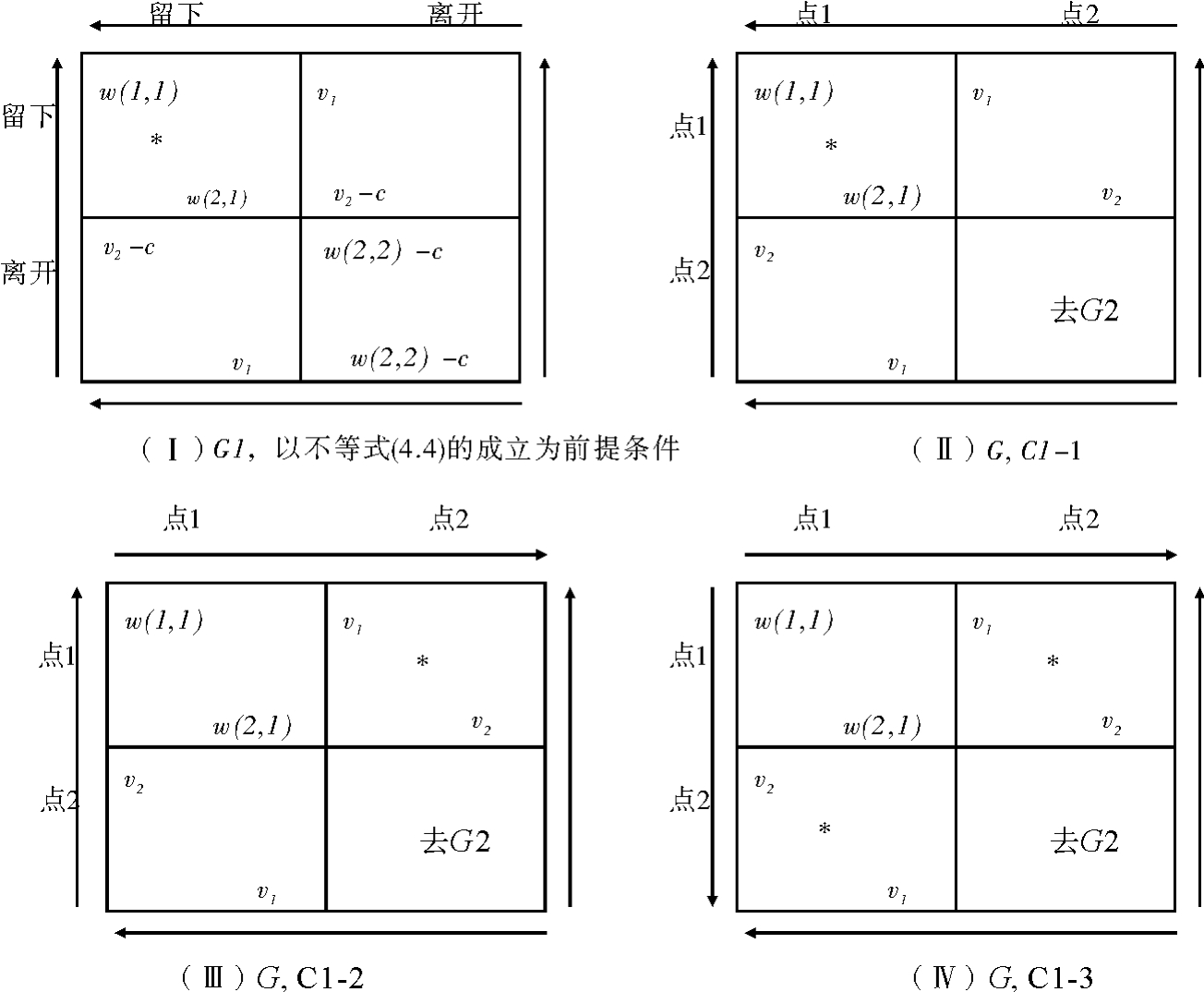
现在来考察继续博弈G1的第二个箭头图表,如图4.4Ⅰ所示。这时子博弈G1只对应一个博弈G。
代表均衡
图4.4 C1-4
情况C1-4。在继续博弈G1中,局中人2顶端的箭头指右,局中人1左边的箭头指上。也即局中人2更愿意离开点1,而不是为它争斗,局中人1则更愿意争斗而不是离开。下列不等式描述了这种情况
w(1,1)>v2-c
w(2,1)<v2-c (4.8)(https://www.daowen.com)
见图4.4Ⅰ。子博弈G1的均衡是局中人1留下来,局中人2离开。这与我们的直觉判断非常吻合,由于局中人1为点1争斗的预期收益值与局中人2为此点争斗的预期收益值存在差异w(1,1)-w(2,1),因此,局中人1之于局中人2的力量优势必定是非常大的。
我们现在把“去G1”这个结果代入博弈G。如图4.4Ⅱ。由于局中人1又有去点1的支配策略。局中人2最好还是去点2。此时的均衡是力量较强的人去收益较好的点。导致子博弈均衡结果(即较强的局中人选择留在较好点)的原因,与促使较强的局中人首先选择较好的点的原因完全相同。
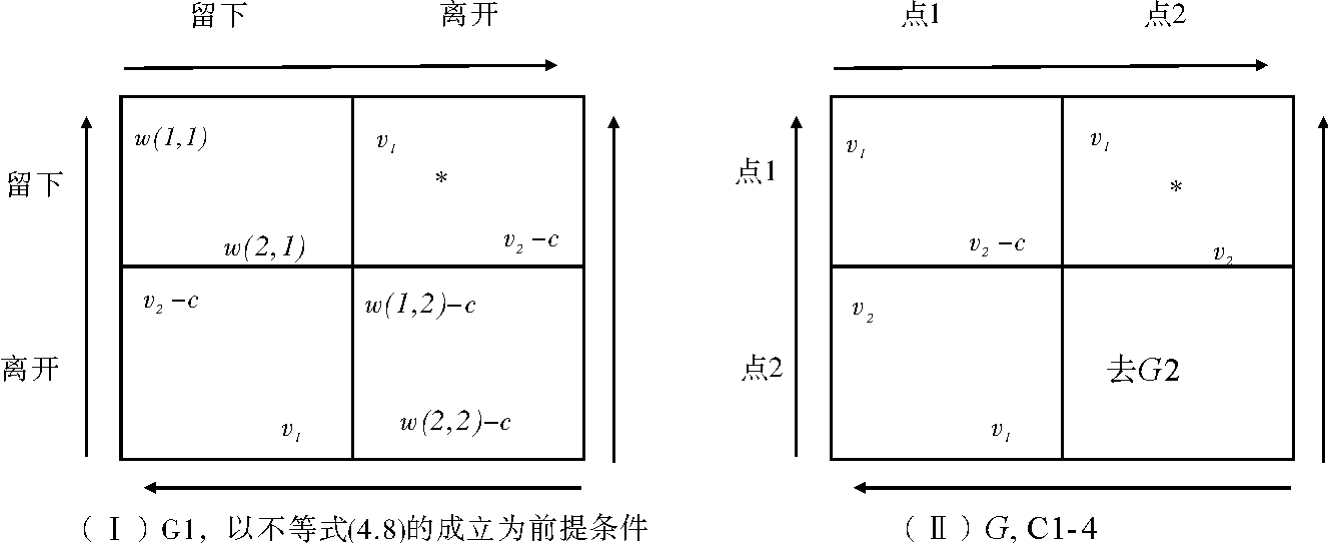
我们现在分析博弈G1第三个也是最后一个箭头图表,如图4.5Ⅰ所示。这个继续博弈也只有唯一对应的博弈G。
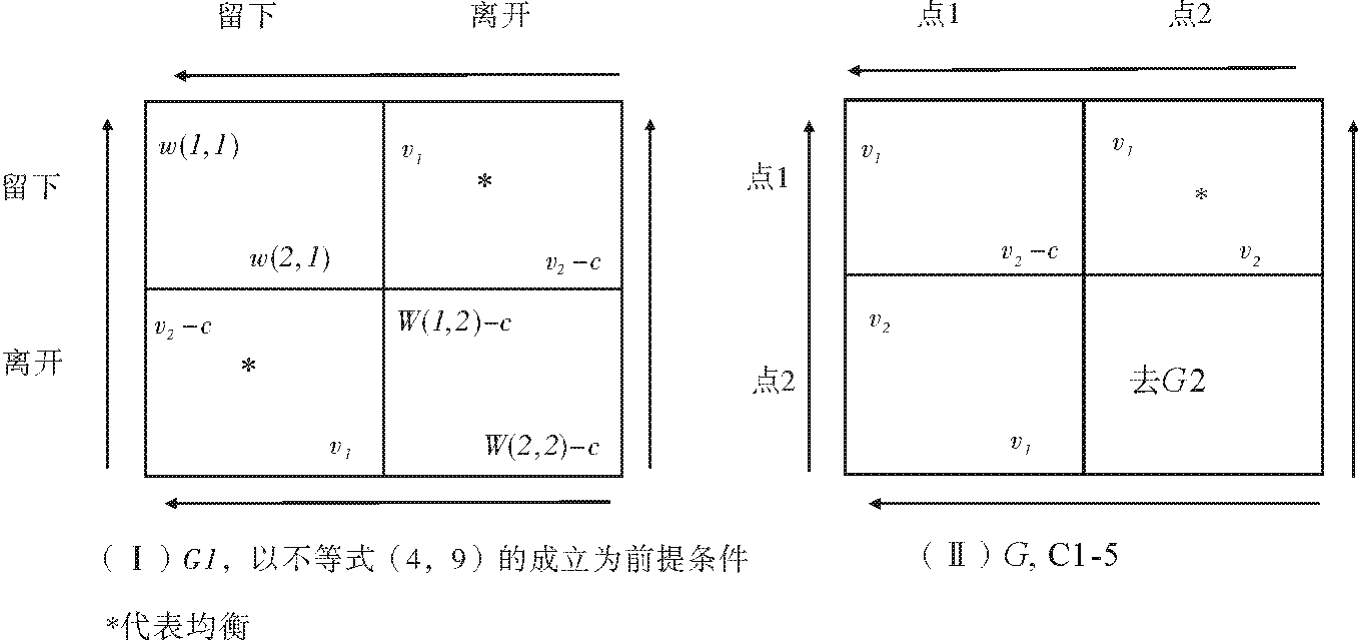
图4.5 C1-5
情况C1-5。现在要考察的最后一种情况是,局中人2在G1顶端的箭头指右,局中人1在左边的箭头指下(见图4.5Ⅰ)。导致这一情况的不等式为
w(1,1)<v2-c
w(2,1)<v2-c (4.9)
根据上述收益关系为前提条件,最后形成的是胆小鬼博弈。如我们先前已探讨的那样,这种博弈有三个均衡。纯粹策略均衡(留下,离开)对应格言“强者即正义”。即较强的局中人得到较好的点;另一个纯粹策略均衡(离开,留下)对应另一格言“弱者即正义”。跟前面的情况一样,混合策略均衡的结果可信程度较低。因此,根据同样的推理逻辑,“去G1”的结果的均衡状态是(留下,离开)。
再转到初始博弈G,我们来看图4.5Ⅱ中的矩阵图。局中人1的支配策略是去点1。有鉴于此,局中人2去点2。在此情形下,又是“强者即正义”规律在发挥作用。
表4.2对上述有争斗的捕鱼分配博弈分析进行了总结。在自然状态C1-1下,两个渔民都去较好的点并发生争斗;在自然状态C1-2至C1-5下,较强的渔民去较好的点。其中,问题尤为棘手且需要变革的状态是发生争斗的C1-1。这激发了我们的下一轮博弈。
表4.2 规则体系下的集体结果和集体收益

规则体系C2
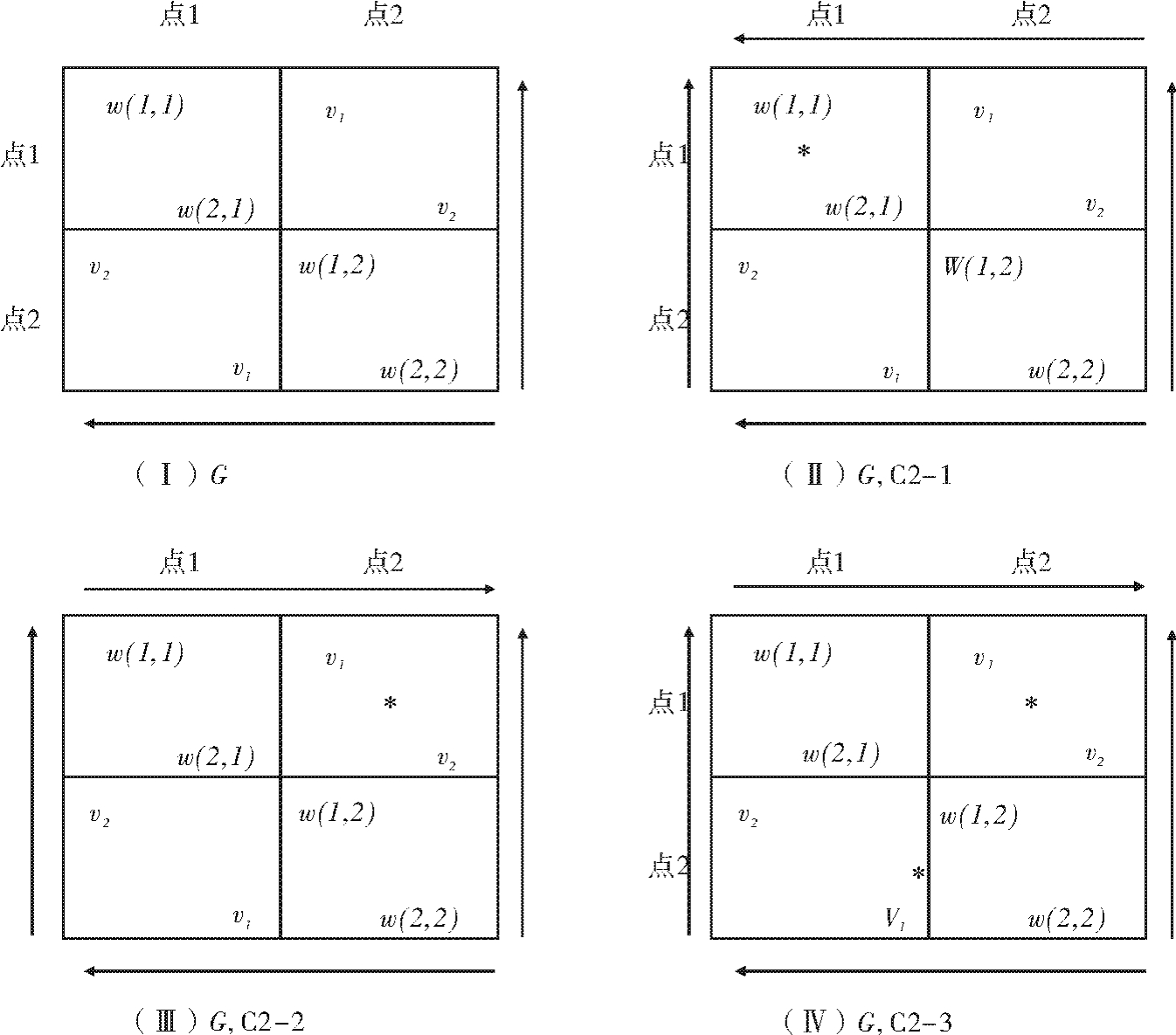
我们现在分析规则体系C2。在这个规则体系中,第一个到达捕鱼点的渔民拥有在当天独占此点捕鱼的权利。后到者不能在此捕鱼,他只能离开已被提取的捕鱼点,去另一个点。与C1一样,C2规则体系下每个渔民同时对在哪个点上捕鱼作出决定。当两个渔民选择的捕鱼点为同一个时,哪个人会成为先到者是随机决定的。这里有两个位置,局中人1与局中人2。设局中人1成为先到者的概率是P;局中人2成为先到者的概率是1-P。机会垂青局中人1,P>0.5。局中人1选择点1的预期收益的计算过程如下:概率P发生时,局中人1为先到者,获得收益v1;1-P概率发生时,局中人1为后来者,需要移到点2,其所能获得的收益是v2-c。因此,局中人1的预期收益值为P v1+(1-P)(v2-c)。这是局中人2也去点1的时候,局中人1对去点1的预期收益,我们把它记做w(1,1);局中人2选择点1的预期收益的计算过程与局中人1相同:概率1-P发生时,局中人2为先到者,获得收益v1;概率P发生时,局中人2的收益为(v2-c)。我们把局中人2的预期收益记做w(2,1)。我们也可以采用同样的方法计算出局中人选择点2的预期收益。我们有意使用了与C1中相同的符号来代表概率与收益——只是解释有所不同。图4.6Ⅰ反映的就是根据以上条件建构的博弈G。
对这个博弈,首先要注意:v1>P v1+(1-P)(v2-c)=w(1,1)。同样,v1>w(2,1)。与可能不得不离开较好点而去更差的点相比,渔民自己拥有较好的点当然更好些。这个变量关系决定了图4.6Ⅰ两个箭头的方向。局中人2底端的箭头指左,局中人1右边的箭头指上。从图中,我们可以看出,在这个博弈中(点2,点2)不是均衡。
根据自然参数(v1,v1,c)的取值,我们需要考察三种情况。如图4.6Ⅱ-Ⅳ所示。
情况C2-1。在这种情况下(见图4.6Ⅱ),局中人2在矩阵顶端的箭头指左,局中人1在矩阵左边的箭头指上。与此情况对应的不等式如下
w(1,1)>v2
w(2,1)>v2 (4.10)
例如,如果P近于0.5,点1比点2有价值得多,这种情况就会发生。对两个局中人来说,均衡是都去点1,让机会来决定谁是先到者(并留下),谁是后到者(并离开)。
情况C2-2。在这种情况下(见图4.6Ⅲ),局中人2在矩阵顶端的箭头指右,局中人1在矩阵左边的箭头指上。与此情况对应的不等式如下
代表均衡
图4.6 依据规则体系C2建构的博弈
w(1,1)>v2
w(2,1)<v2 (4.11)
例如,如果P近于1,而且c很大,这种情况就会发生。均衡是局中人1去点1,局中人2去点2。局中人1成为先到者的机会大得足以使局中人1一直得到点1。
情况C2-3。在这种情况下(见图4.6Ⅳ),局中人2在矩阵顶端的箭头指右,局中人在矩阵左边的箭头指下。与此情况对应的不等式如下
w(1,1)<v2
w(2,1)<v2 (4.12)
例如,如果P近于0.5,而且两个点的价值几乎均等,这种情况就会发生。这时的博弈为胆小鬼博弈。这里的推导过程与前文有关不对称胆小鬼博弈的推导一样,因此博弈的均衡状态是:局中人1去点1,局中人2去点2。更有可能抢先到达较好点的局中人去较好的点。
总结规则体系C2的各个结果,我们可以看出,运用“先到者,权利优先”原则确实可以消除争斗。该原则甚至能使三种自然状态中的两个实现最大的集体收益v1+v2。然而,在某一个点的优势特别明显时(情况C2-1),社会收益没有最大化,为w(1,1)+w(2,1)=v1+v2-c。由此可见,这个规则体系仍有改进的余地(见表4.2)。
规则体系C3
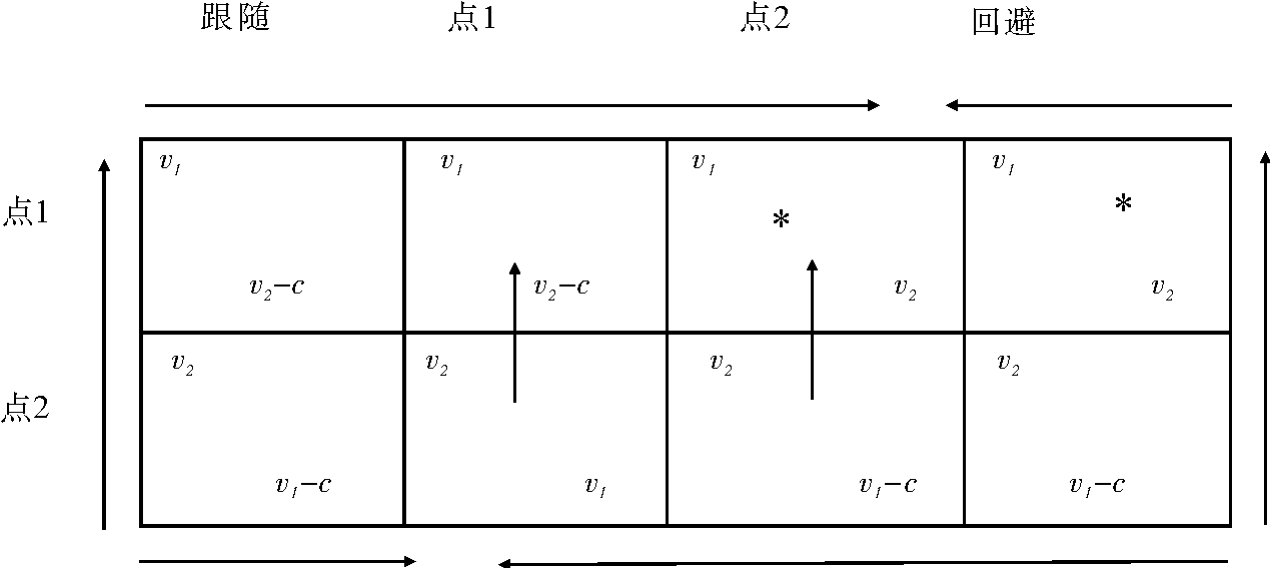
现在分析规则体系C3。有两个位置:局中人1(宣告某一个点)与局中人2(听见他人的宣告)。与在C2中的情况一样,第一个到达捕鱼点的渔民获得这一天“专享”在此点的捕鱼权利。另一个渔民,无论是谁,都要自动离开已被占领的点,去另一个点。与C2不同的是,作出宣告的局中人总是首先到达该点。而且宣告一个点就意味着局中人承诺要去那个点。在这个博弈中,两个局中人可的备选策略是不同的。局中人1的两个策略是(宣告点1,宣告点2)。局中人2的完整计划包括任何可能发生的行为。因此,对局中人2而言,有四个可能的策略:
如果局中人1宣告点1,去点1(跟随)。
如果局中人1宣告点2,去点2。
这是“跟随”策略。这个计划的内容是,无论局中人1作出什么宣告,局中人2都去前者所宣告的那一点。
如果局中人1宣告点1,去点1(点1)。
如果局中人1宣告点2,去点1。
这是“点1”策略。这个计划的内容是,不管局中人1作出什么宣告,局中人都去点1。
如果局中人1宣告点1,去点2(点2)。
如果局中人2宣告点2,去点2。
这是“点2”策略。这个计划的内容是,不管局中人1作出什么宣告,局中人2都去点2。
如果局中人1宣告点1,去点2(回避)。
如果局中人1宣告点2,去点1。
这是“回避”策略。这个计划的内容是,局中人2将不去局中人1所宣告的点。现在可以得出图4.7的矩阵。
这是我们第一次遇到非正方形的矩阵。这种矩形图的生成是因为可用策略的不对称性。首先我们要注意局中人1拥有宣告使用点1的支配策略。该局中人所有的箭头均指向上方。有两种纯粹策略均衡:(宣告点1,点2),和(宣告点1,回避)。这两种均衡具有相等的观察效果:两者的结果相同。有权宣告的一方占有最佳点。同时需要特别指出的是,对自然参数(v1,v2,c)所可能的取值而言,这个结果都实现了集体收益的最大化。最终,我们发现了一个可以解决所有自然状态下的公共池塘资源问题的规则体系。
规则体系C4
一次性公共池塘资源问题一旦得到了解决,如何解决重复发生的公共池塘资源问题的问题就产生了。规则体系C4是把C3运用到重复性的分配问题上。为简便起见,我们考察发生两次的捕鱼博弈。在C4,两个局中人轮流享有宣告权。捕鱼博弈发生的第一次,由局中人1宣告;第二次,由局中人2宣告。均衡序列是局中人1在第一个阶段宣告点1,局中人2的均衡序列是在第二个阶段宣告点1。[17]每个局中人平均得到的重复博弈收益是v1+v2/2。这样,一次性公共池塘资源问题的解决方案,就可以历久长存下去了。
代表均衡
图4.7 依据规则体系C 3构建的博弈
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






