第二节　两个局中人与两个策略的公共池塘资源博弈

本节将运用博弈理论分析四个博弈。这四个博弈分别针对的是公共池塘资源困境的四个方面:(1)提取的外部性;(2)分配;(3)资源提供;(4)监督。每一个方面的分析都证明，博弈结构的变化能够带来与预测的策略行为截然不同的均衡。这说明，我们确实有必要认真考察实地场景中或以普通模型为基础的政策决策情境。

1.提取的外部性

我们在第一章就曾指出，对公共池塘资源的基本预测是:局中人会忽略自己的投入决策对其他人从公共池塘资源获益情况的影响。这种提取的外部性正是导致对公共池塘资源被过度提取的根源。下面我们来就这个问题的简化情境——即有两个局中人、每个局中人都有两个策略——建立博弈模型。两个局中人分别是公共池塘资源的提取者。每个局中人都有以代币为单位的一个单位的生产性投入(代表其劳动、资本或两者兼而有之)。无论另一个局中人作出何种选择，其中的一个局中人把代币投资到安全的外部机会，会得到收益w。这就像挣工资的人在博弈结构外工作一样。局中人也可以把自己的代币投入到公共池塘资源，相关的问题当然会因此变得更加复杂。设x_i为局中人i投资于公共池塘资源的代币数。那么x_i=0指利用外部机会，而x_i=1指投资于公共池塘资源。公共池塘资源的产出是局中人总投资的函数，F(∑x_i)。人们从公共池塘资源获取资源的份额与他们对公共池塘资源的投入成比例。因此，当局中人i没有投资于公共池塘资源时，其公共池塘资源产出额为0;当他(或她)投资于公共池塘资源时，产出额就为(x_i/∑x_i) F(∑x_i)。这样，就形成了图3.4Ⅰ所代表的博弈。

我们现在来对该博弈进行求解。博弈的解取决于——如我们所观察的那样——w、F(1)与F(2)/2的关系。如果公共池塘资源的投入收益率会随着投资规模扩大而递减，那么我们就可以暂时假设F(2)/2＜F(1)。只要公共池塘资源具有一定的经济价值，那么F(1)＞w。这时，将第一个代币投资于公共池塘资源是有利的。根据以上两个条件，我们得到图3.4Ⅰ的箭头模式，可以看出，无论对于哪个局中人来讲，x_i=0都不会成为纳什均衡的组成部分。纳什均衡点上发生的事情取决于公共池塘资源的半个份额F(2)/2与外部机会w的关系。假设公共池塘资源的收益率急剧减少，出现F(1)＞w，w＞F(2)/2的情况，那么我们就会得到图3.4Ⅱ中的箭头模式，此时有两个均衡。两个均衡的结构都是:一个局中人投资于公共池塘资源，另一个置身局外，且投资于公共池塘资源的局中人比置身局外的局中人赢利更多。这就是一个胆小鬼博弈的具体例子。

另外一种可能性是:公共池塘资源不会如此快地拥挤起来，而且F(2)/2＞w。图3.4Ⅲ表示的就是这种情况。此时存在着唯一的纳什均衡，即两个局中人都投资于公共池塘资源。此类情境会让人联想起囚徒困境，因为每个局中人都拥有支配策略，但它可能并不是什么悲剧。悲剧存在与否或存在程度(如果存在悲剧的话)，取决于F的具体特性与w的价值。例如，若F是一个递增的凸函数——比如在F=(∑x_i)²且w＜1的情况下，那么两个局中人都投资于公共池塘资源所拥有的结果就是所有可能情况中最好的。另一方面，若F是严格意义的凹函数，那么公共池塘资源两个局中人的结果就可能出现社会低效率。假设F为平方根的函数，且w=0.7。那么局中人的收益关系取值情况即为a=0.707，b=1，c=d=0.7(参看图3.2)。如果两个局中人都投资于公共池塘资源，集体总收益为1.414，远小于只有一个局中人投资于公共池塘资源时的总收益的值1.7。这的确是公共池塘资源困境。由此可见，要变成囚徒困境，需要外部机会(w)的取值与公共池塘资源生产函数(F)同时具备相当特殊的条件。

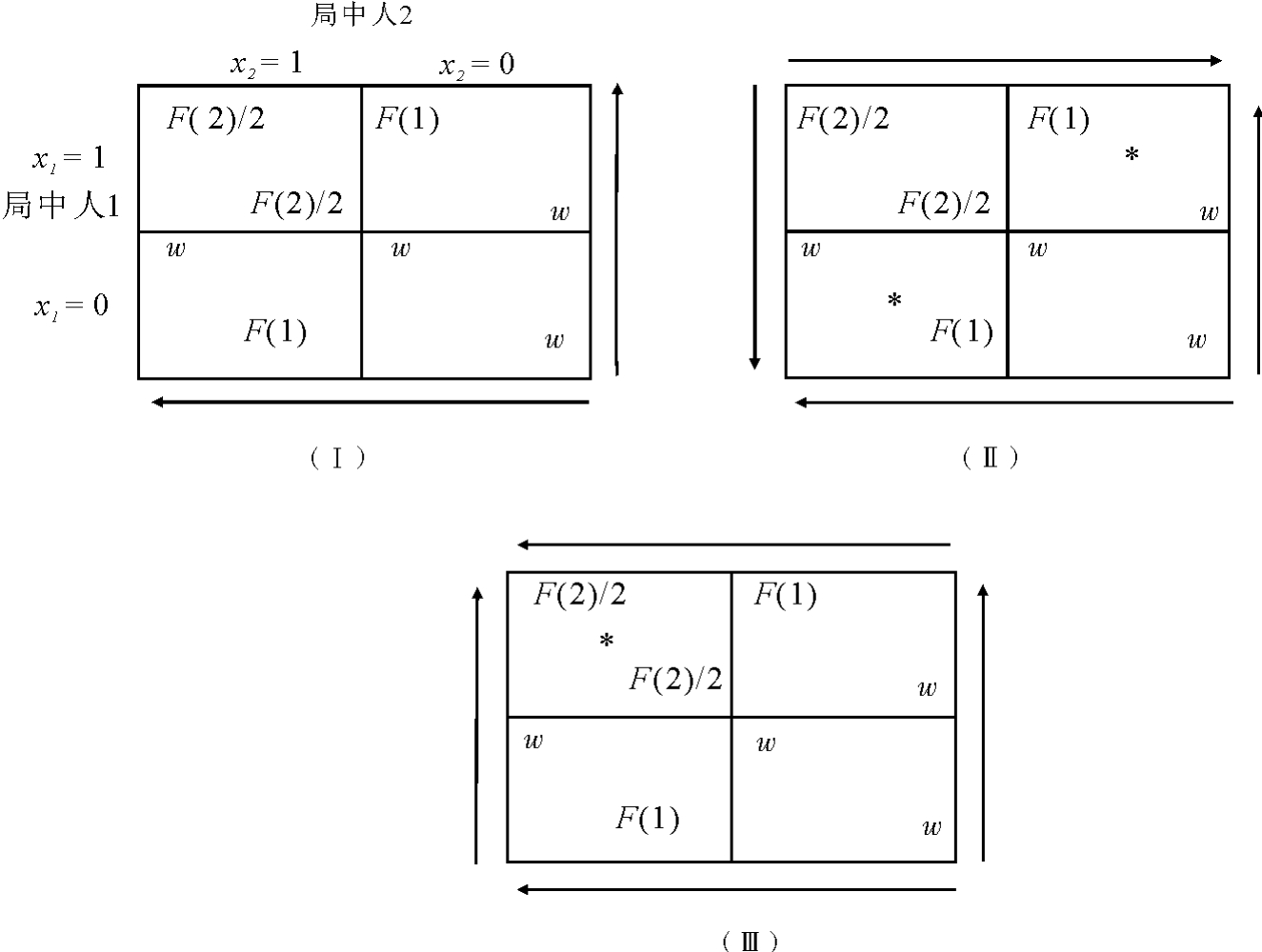
*代表均衡

图3.4　提取的外部性

2.分配问题

当局中人面临在生产收益上具有差异的各个“提取点”时，他们就会遇到分配问题。分配问题的最简单例子是我们下面要来讨论的博弈。公共池塘资源，例如捕鱼场，由两个已知价值为v_i的点构成。点1的捕鱼价值大于点2的捕鱼价值:v₁＞v₂。此时有两个使用者。每个使用者可以使用同样的点，这时两人分享其价值。图3.5Ⅰ反映的是两人的非合作博弈，图中的箭头显示:两个局中人都在坏点2上捕鱼的策略组不是均衡状态。

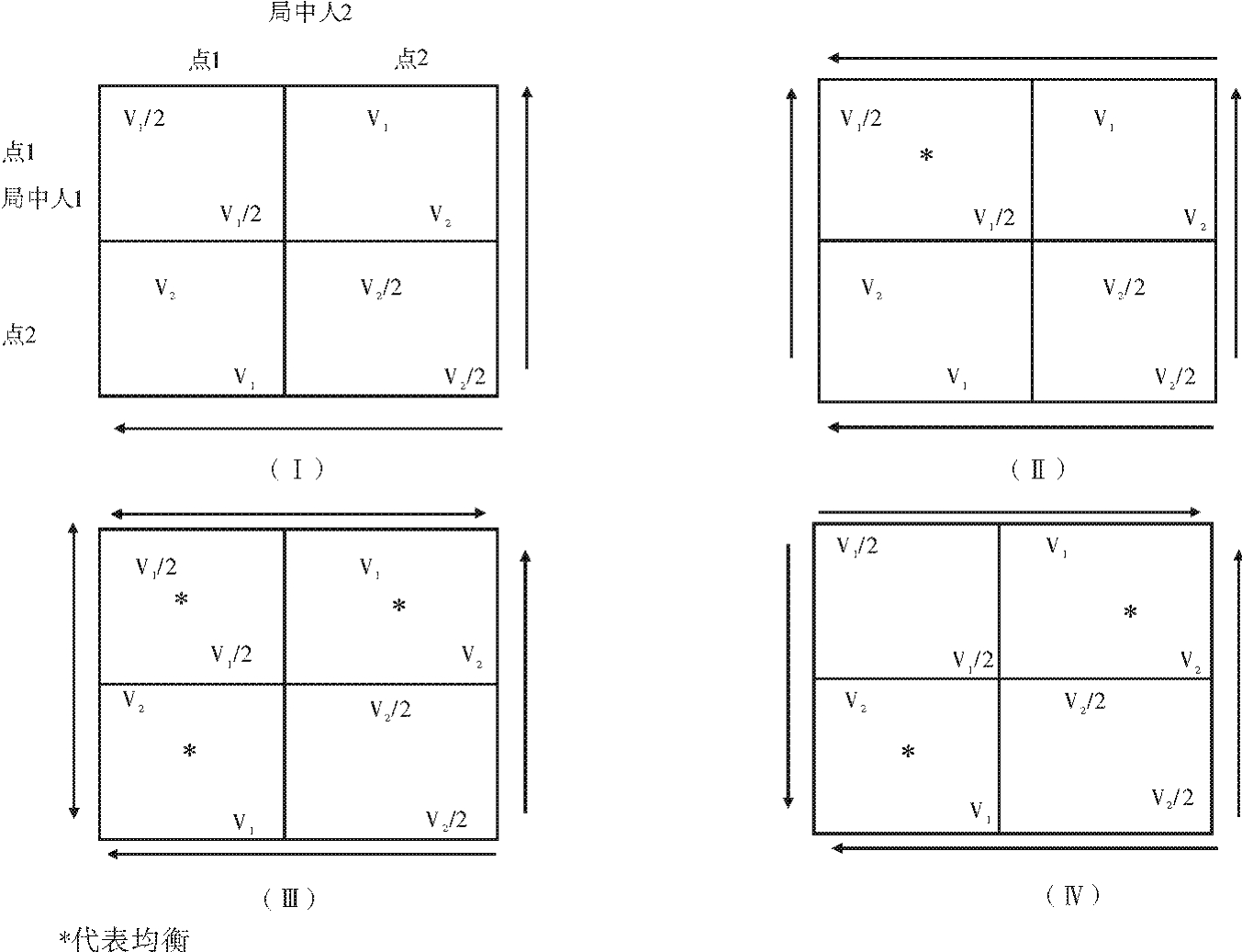
图3.5　分配博弈

我们需要考虑两种主要情况与一种边界情况。其中一种主要情况是v₁＞2(v₂)，这时，好的点的价值要远远好于坏的点。如图3.5Ⅱ所示，局中人1有一个箭头在矩阵左边从下往上指向点1，局中人2有一个箭头在矩阵上方从右向左指向点1。因为点1总是好于点2，因此，每个局中人还在矩阵的右边和下方都有一个箭头背离点2。根据图中的箭头符号可以看出，每个使用者都拥有支配策略，即选择使用点1。因此，这个模型中存在唯一的均衡点，即两个渔民总是在最好的捕鱼点作业。不过，这样的结果总是有问题的。因为两个渔民都在同一个捕鱼点上，所以局中人的总收益是v₁。然而，渔民理想状态的总收益关系为v₁+v₂。对整个集体来说，这样的博弈结果不是最优的。

边界情况是v₁=2v₂。每个公共池塘资源使用者仍拥有支配策略，即使用点1。因此，点1上的两个局中人继续保持均衡。然而，现在我们第一次有了双箭头。如果局中人2在好的点上，局中人1就不需要在意自己在哪个点上捕鱼。图3.5Ⅲ矩阵左边的双箭头就反映了这种情况。对局中人2也是如此。现在有三个纯粹策略均衡，其中两个实际上避免了公共池塘资源困境(记住，如果两个箭头都指向一个结果，则结果为均衡)。

在另一种主要情况下，v₁＜2 v₂。图3.5Ⅳ显示了箭头图表。这也是一个胆小鬼博弈的例子。两个局中人都没有支配策略。这时，存在两个纯粹策略均衡，即一个点上只有一个局中人，集体收益最大化。然而，我们不能乐观地期望因为这种分配问题，集体收益就一定会实现最大化。这个博弈中只有一个位置，即渔民。只有一种位置的博弈是对称博弈。每个对称的博弈都有对称的均衡。由于这个分配博弈的情境在本质上是对称的，因此，局中人可能并不愿意接受不对称均衡造成的不平等的收益关系。而经常使局中人处于不对称位置的私有财产或习俗等制度，正好是这个博弈里没有涵盖的内容。

分配博弈的对称均衡涉及概率的问题。每个对称均衡具有的共性是:局中人获得相同的收益，并使用相同的策略。我们现在就来计算分配博弈对称的混合策略均衡。进行必要计算的最好方法是举例。假设v₁=8，v₂=6。局中人都不能确定另一个人要做什么，但是，他们知道另一个人有一定的概率会处于其中的某一个点上。假设这个概率对每个渔民都一样，并记为P，因此，P表示去点1的概率，1－P表示去点2的概率。在混合策略均衡点上，局中人对去两个点中的哪一个毫不关心。为实现这一点，首先要计算去点1的预期收益值。当概率为P时，有人已经到那儿了且收益值为4;概率为1－P时，没人去那里，收益值为8。相加后，去点1的预期收益值是4P+8(1－P)=8－4P。现在以同样方法计算点2的预期收益值。当概率为P时，没人在那里(他们去了点1)，收益值为6;概率为1－P时，有人在那里且收益值为3。相加之后，去点2的预期收益值是6P+3(1－P)=3+3P。在均衡状态时，去点1的预期收益值等于去点2的预期收益值，即8－4P=3+ 3P。经过计算，去点1的概率应为P=5/7;去点2的概率为1－P=2/7。每个点的预期收益值就是8－4(5/7)=3+3(5/7)=36/7。注意，即使局中人现在的收益相同，都是36/7，但他们获得的收益要低于最差点的收益6。这是一个比囚徒困境还要微妙的公共池塘资源困境，但一样也存在问题。

3.资源提供

很多公共池塘资源的使用者都面临着提供资源(例如挖掘灌溉沟渠)或维护资源的问题(修护灌溉沟渠)。有关这类问题的决策，可以作为纯公益物品的提供来建立模型。下面，我们将举例说明这个问题是如何转化为囚徒困境或承诺博弈的，其中的影响变量是提供技术的细节。

假设有两个局中人。每个局中人拥有在自愿的前提下为资源提供贡献一个单位的投入(以代币计量)。如果代币没有被投入到资源提供上，则有外部值w。如果为资源提供投入代币，局中人的收益为v。设x_i是局中人i投入到公共池塘资源提供的代币数。x_i=0则表示利用外部机会，x_i=1表示为公共池塘资源提供做贡献。从公共池塘资源提供得到的收益与局中人的总贡献成正比，即Σx_i。不管局中人是否对资源投入有所贡献，局中人从公共池塘资源提供得到的收益都是v(Σx_i)。图3.6显示了此情境下两个可能的博弈。

首先，如果2v＞w＞v，那么结果是囚徒困境。每个局中人都拥有选择不投入的支配策略，但是两个都投入，两人的境况都会更好。见图3.6Ⅰ。如果2v＞v＞w，在这种情况下，投入的激励会非常强，每个局中人都拥有选择投入的支配策略，且均衡上的公共池塘资源函数呈现最优形式。见图3.6Ⅱ。

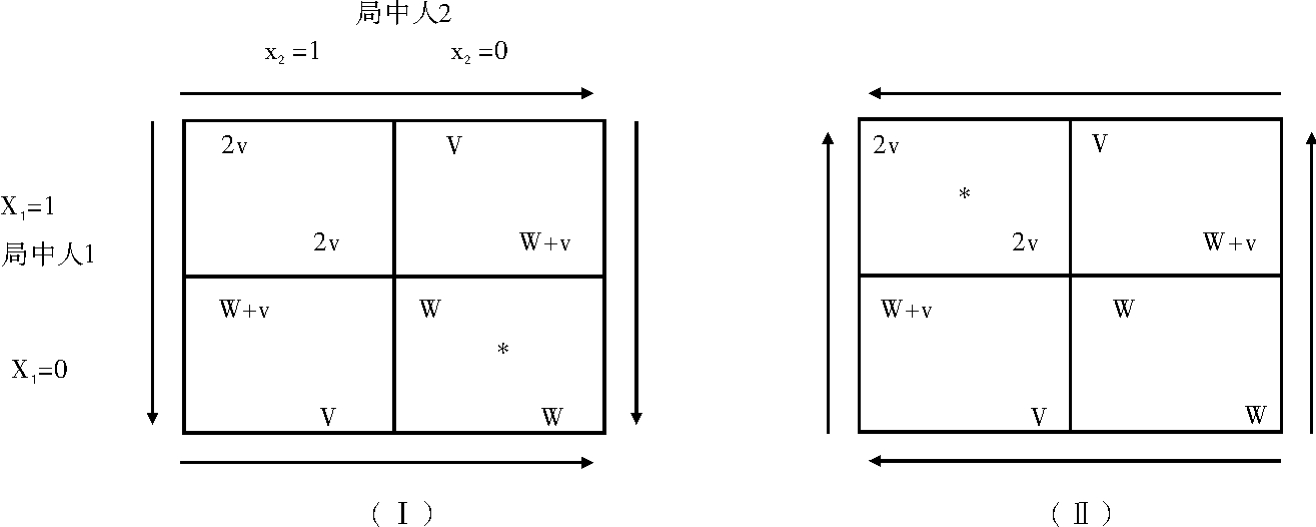
*代表均衡

图3.6　有中间值的提供博弈

现在，我们将博弈条件按下面的方式做一下改变。如果只有一个代币被贡献出来用于资源提供，那么，由于资金不足，贡献出来的代币的价值回报仍是0。这种情况可能发生在被提供的物品具有独立形式这样的自然环境下(例如，不完整的桥梁是没有价值的)。由于其放弃了外部的机会，唯一一个将代币投入到提供活动的局中人，获得的收益为0。如果两个代币都被贡献了出来，那么价值回报与以前一样，是2v。提供技术上的这种变化将导致图3.7Ⅰ的博弈。图中的箭头表示:无论v或w的取值是多少，总是存在一个两个局中人都选择不投入的均衡。如果你知道另一个局中人会选择不投入，那么你也应该作出同样的选择。

除了没人投入这样的均衡外，还可能存在另一种纯粹策略均衡。首先假设2v＞w。此时，其中一个人投入代币就是对另一个人选择投入的激励。因此，不仅有两人都不投入的均衡，也有两人都投入的均衡。这就是承诺博弈的例子(图3.7Ⅱ)。严格地讲，对局中人的收益而言，两人都投入的均衡要好于两人都不投入的均衡。另一种情况是2v＜w，此时的支配策略是不投入，因此存在唯一的均衡(图3.7Ⅲ)。需要说明的是，这种情况不是囚徒困境:提供资源的投入回报是如此低，以至局中人能做的最好的选择就是不提供资源。(www.daowen.com)

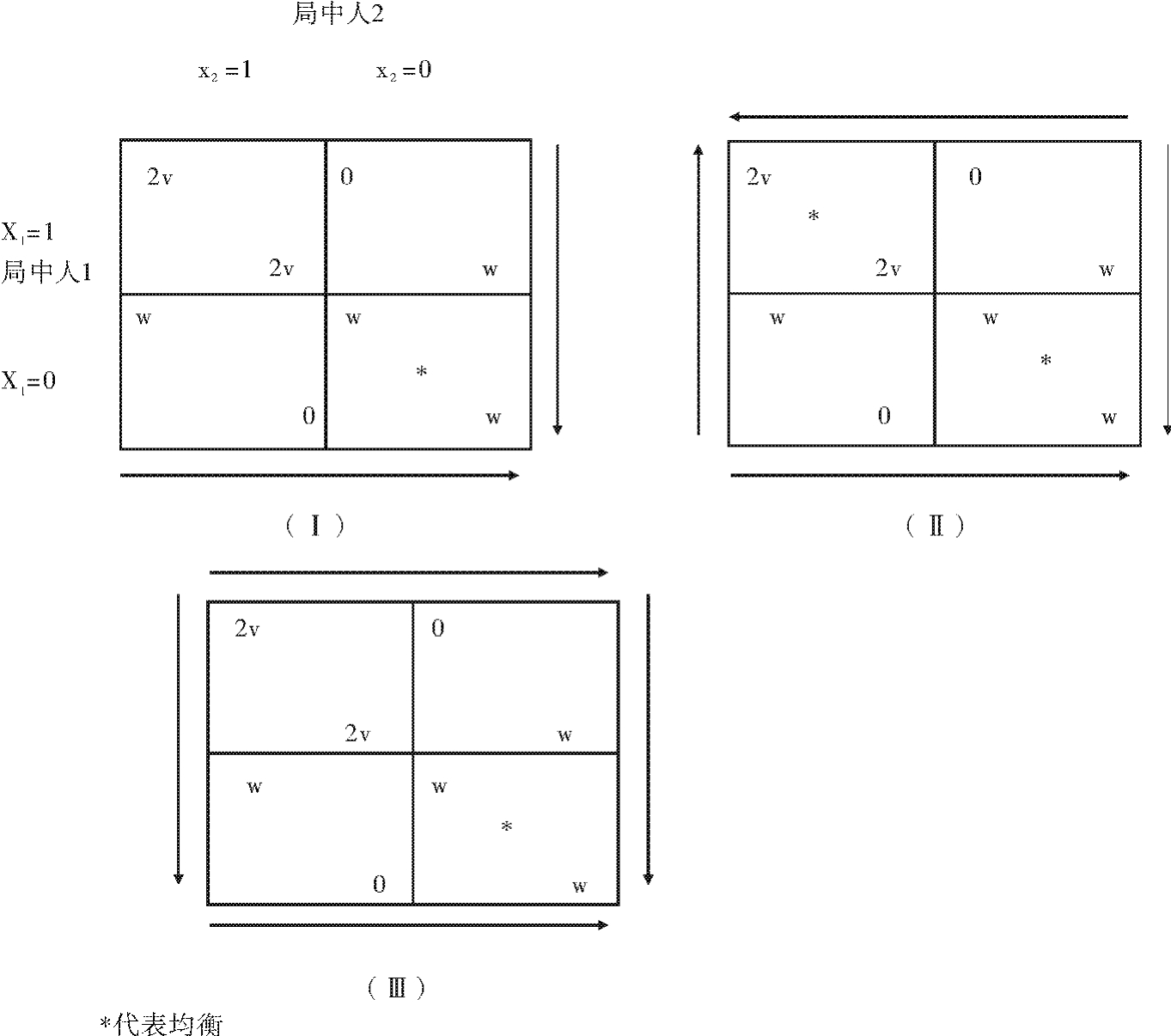
图3.7　没有中间值的提供博弈

4.监督

到目前为止，我们给出的每个例子中都只有一个位置:提取外部性博弈的提取者、分配博弈的渔民与资源提供博弈的投入者。现在我们放宽这种限制，来研究有两个不同位置的博弈。位置取决于灌溉系统的自然形式，灌溉系统中处于首端的局中人比处于末端的农民先获得水流。然而，末端的农民有机会监督首端的人的行为。局中人1是处于系统首端的局中人，其策略是获取自己应得的水，或是获取超过自己应得份额的水。局中人2是处于系统末端的人，其策略是监督或不监督局中人1的所作作为。当局中人1取走自己的应得份额，且局中人2没有监督时，此时的收益关系为(0，0)。事实上，在这个博弈中，局中人可能获得的总收益的最大值为0。

若局中人1取走过量的水，则他从额外的水中得到正收益B。如果与此同时，局中人2没有进行监督，那么被取走的水就从流量中失去了，局中人2则丢掉了那部分水的收益，其收益为－B。另外，若局中人2选择对局中人1的行为进行监督，需要花费C作为监督费。如果局中人1只取走自己应得的份额，而局中人2选择监督，那么两个局中人的结果是:局中人1收益为0，局中人2的收益为－C。现在，我们假设局中人1取走过量的水且局中人2进行监督。这时，由于局中人2所用的侦察技术不完美，有时他能发现局中人1取走了过量的水，有时则没能发现这种情况。局中人2在监督时发现局中人1取走过量水的概率为P，没有发现的概率为1－P。在概率P发生的情况下，局中人2追回了被局中人1取走的过量的水并由于成功监督而得到奖金M;局中人1，除了还回过量的水外，还由于被抓住而支付罚金F。在概率1－P发生的情况下，即局中人2进行监督，但并没有发现什么。此时，局中人2付出了监督成本但什么也没发生。我们现在来计算这个结果的预期收益关系。对局中人1，因侦察而被发现的概率P发生时，此时收益为－F;侦察没有发挥作用的概率1－P发生时，此时收益为B。因此，对局中人1而言，预期收益值是P(－F)+(1－P)(B)=B－P(F+B)。对局中人2而言，侦察发挥作用的概率为P，收益为(M－C);侦察没有发挥作用的概率是1－P，收益为(－B－C)。因此，局中人2的预期是P(M－C)+(1－P)(－B－C)=PM－［C+(1－P)B］。这就是图3.8中的监督博弈的收益关系。

监督博弈是目前我们所考察过的最复杂的博弈。^[5]它有四个各不相同的完整的箭头图表，其中的影响变量是收益关系参数。当局中人1取走自己的应得份额时，对局中人2来说，箭头总是指向“不监督”。因此，这对策略(局中人1取走份额，局中人2监督)永远不可能是均衡。而且，当局中人2不监督时，对局中人1来说，箭头总是指向“取走多于应得的份额”，因此，这对策略(局中人1取走应得份额，局中人2不监督)也不会是均衡。图3.8中的箭头反映的就是这种情况。由于矩阵左边的箭头可能指上或指下，底端的箭头可能指左或指右，因此，对于图3.8所描述的博弈，我们又可以具体分为四种情况来进行详细讨论(见图3.9)。

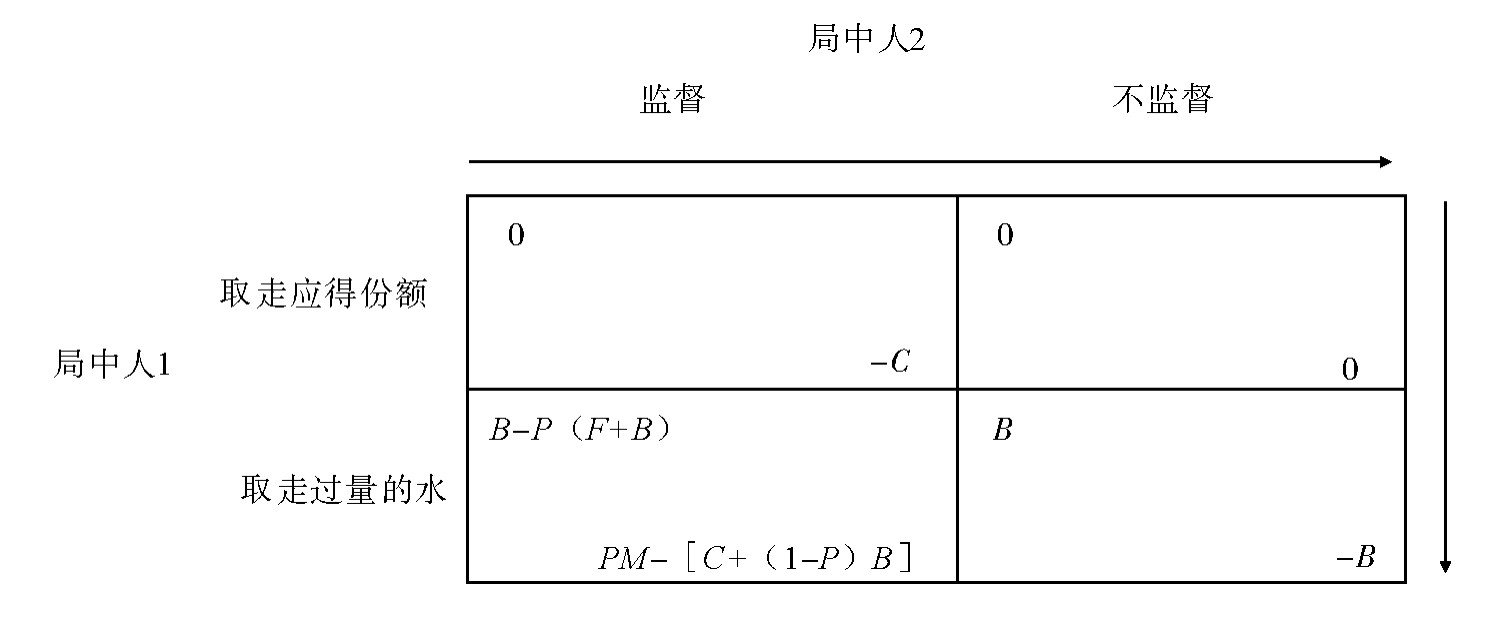
图3.8　监督

情况1:现在考察图3.9Ⅰ。左边箭头指下，底端箭头指左。这个案例的参数条件是B＞P(F+B)(左边箭头指下)与P(M+B)＞C(底端箭头指左)。对局中人1而言的均衡，就是取走多于自己应得份额的水，对局中人2而言的均衡是监督。这是一个纯粹策略的不对称均衡。即使局中人1知道自己的行为会受到监督，但他仍毫不犹豫地取走过量的水。

情况2:考察图3.9Ⅱ。左边箭头指下，底端箭头指右。这个案例的参数条件是B＞P(F+B)(箭头指下)与P(M+B)＜C(箭头指右)。局中人1的均衡是取走多于应得份额的水，局中人2的均衡是不监督。这是一个纯粹策略的不对称均衡。在这个参数构造下，监督的策略可能性对取过量水的诱惑没有影响。能最终导致灌溉系统由第一种情况变为第二种情况2的两个变化是:监督的成本C增加或者发现的概率P减少。

情况3:考察图3.9Ⅲ。左边箭头指上，底端箭头指右。这个案例的参数条件是B＜P(F+B)(箭头指上)与P(M+B)＜C(箭头指右)。局中人1的均衡是取过量水，局中人2的均衡是不监督。这是一个纯粹策略的不对称均衡。确实，结果与案例2的结果相同，只是箭头方向不同。

情况4:考察图3.9Ⅳ。左边箭头指上，底端箭头指左。这个案例的参数条件是B＜P(F+B)(箭头指上)与P(M+B)＞C(箭头指左)。这里没有纯粹策略均衡:箭头的指向背离每个结果。不过，存在混合策略均衡。要计算这个均衡需要两个步骤。

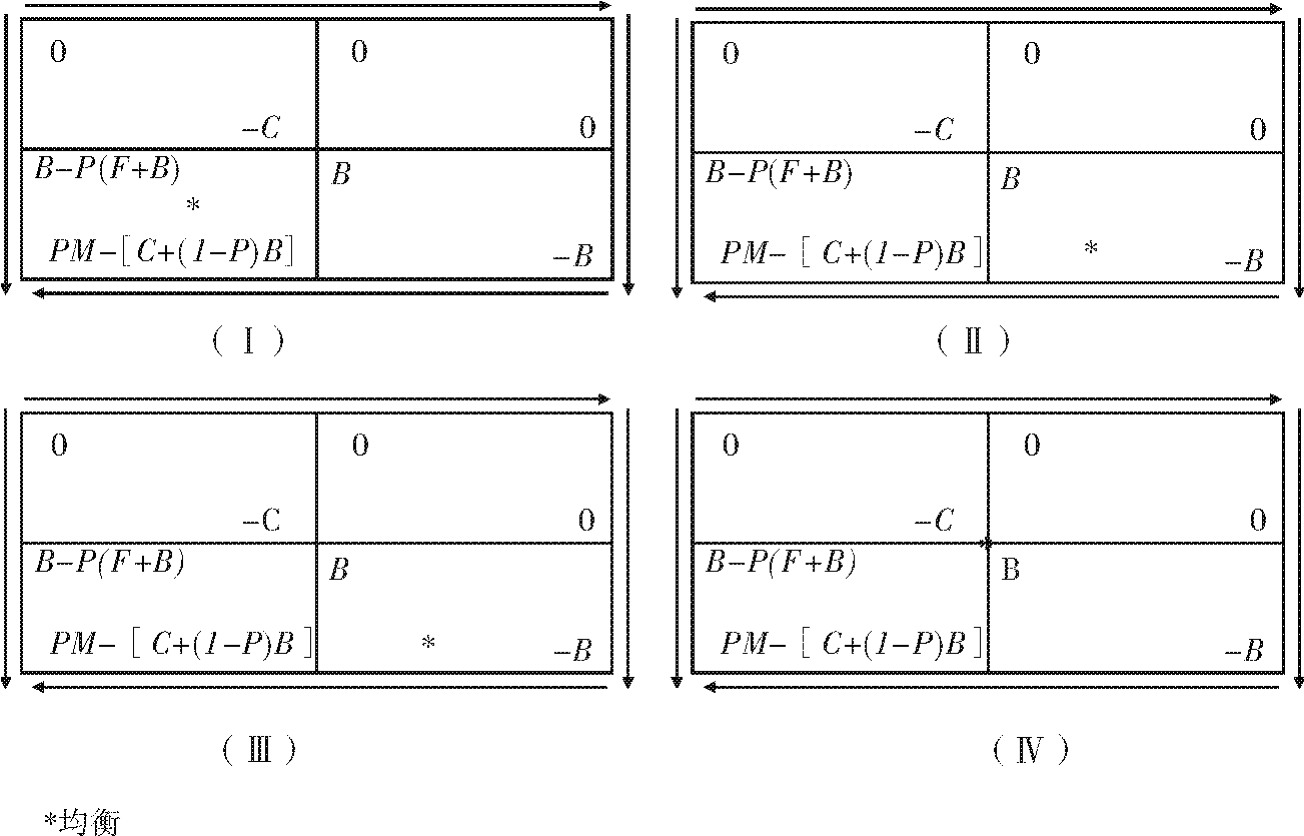
图3.9　监督的四种情况

第一步，在均衡上，局中人2进行监督的概率必须正好足够大，此时局中人1的两种策略(取走应得份额或取走过量水)无关紧要。设m表示监督的概率。如果局中人1取走的恰好是应得份额，则其收益为0。如果局中人1取走过量水，在受到监督的概率m发生时，其收益为B－P(F+B);在不受监督的概率1－m发生时，其收益为B。取走过量水的预期收益值因而是m［B－P(F+B)］+(1－m)B。这个预期收益值必定等于0，即他(或她)取走应得份额的收益:m［B－P(F+B)］+(1－m)B=0。这个方程式的解，即局中人2进行监督的均衡概率，m*。这是局中人2的均衡混合策略。求解m*，我们可以得到m*=B/［P(B+F)］。第二步，局中人1取走过量水的概率必须正好足够大，此时局中人2监督与否已经影响不大。设t为局中人1取走应得份额的概率。在t概率中，局中人2不监督，局中人1取走应得份额，局中人2收益为0的概率为t;在过量取水的1－t概率中，局中人1取走过量水，局中人2获得收益－B。因此，如果局中人2不监督，其预期收益为t(0)+(1－t)(－B)=(1－t)(－B)。如果局中人2进行监督，概率t发生时，局中人1取走应得份额且局中人2获得收益－C;概率1－t发生时，局中人1取走过量水且局中人2获得收益PM－［C+(1－P)B］。因此，如果局中人2进行监督，其预期收益为t(－C)+(1－t){PM－［C+(1－P)B］}。设局中人2监督的收益等于其不监督的收益，会得到下面这个等式:

t(－C)+(1－t){PM－［C+(1－P)B］}=(1－t)(－B)

求解以后，将得到1－t*=C/P(M+B)，其中t*是局中人1正好取走应得份额这个均衡的概率，1－t*是局中人1取走过量水的概率。因此，不对称的混合策略均衡是(m*，t*)。情况4是我们观察的第一个只有混合策略均衡的博弈。

根据以上四种情况的结果可以看出，概括来讲，均衡点上总是存在些许过量取水的趋向。在前三种情况下，局中人1总是取过量的水。在第四种情况下，局中人1也有过量取水的可能性。因此，局中人1处于灌溉系统首端的固有自然优势也就表现为均衡策略优势。

政区示意图是概括博弈均衡分析的有用工具。它可以反映博弈均衡对收益关系参数值的依赖关系，而这种关系反过来又与其背后的自然环境与治理规则有关。图3.10是与前文探讨的监督博弈相对应的政区示意图。图中的横坐标为C，纵坐标为P。图表中有两个边界点。边界点P=B/(B+F)划分的是图3.9左边箭头指上与指下的两种情况;边界点P=C/(M+B)划分的是图3.9中底端箭头指左与指右的两种情况。由于这四种不同情况会形成三种截然不同的可观察到的均衡行为，因此示意图上有三个区域，分别为:“取过量的水、监督”、“取过量的水、不监督”与“混合”。在示意图左边的“取过量的水，监督”区域中，P＜B/(B+F)且P＜C/(M+B)。这两个不等式显然等同于情况1中所界定的条件。情况2与3，在均衡点上的状态是一样的，都反映在政区图中“取过量的水，不监督”这一区域。最后一个被称为“混合”的区域对应的是情况4。这样的政区示意图可以直观地显示出均衡行为是如何取决于自然与收益关系特性的(在这里，即参数P、F、B、M与C)。它也可帮助我们预测，如果这些参数发生大的变化博弈会发生何种变化。一个大变化可能会使博弈均衡从一个政体区域移入另一个政体区域。^[6]

有时，变量变化所造成的后果看来是相当清晰的。不过，由于变量变化带来的明显且主要的效果却往往与次要的效果混在一起，而当我们仅仅做口头推理时，这些次要效果很容易被忽视。我们现在以监督成本C发生变化为例。常规的经济直觉会告诉我们，随着监督成本的增加，监督活动就会减少。但我们现在可以通过政区示意图说明，对C的增加所做出的可能回应是多种的，而并非只有一种。精确的博弈均衡回应取决于系统处于什么样的区域中以及C的增加有多大。

在政区示意图中，C的增加意味着向右移动。我们分以下三种情况来分析:首先，假设系统处于“混合”区域。如果C的增加量很小，那么系统仍将处于“混合”区域。在这个区域的任何地方，监督的概率都相同。有人可能认为，这个结论违反直觉知识;然而，根据我们前面推理所得出的公式m^*=B/［P(B+F)］说明，C在“混合”区域不起作用。另一方面，如果C的增加量很大，系统将离开“混合”区，进入“取过量的水，不监督”区域。监督的概率下降至0。第二，假设系统处于“取过量的水，监督”区域。如果C的增加量很小，系统会仍停留在本区域内且监督的概率没有增加;如果C的增加量很大，系统将进入“取过量的水，不监督”区域，监督概率则下降为0。最后，假设系统处于“取过量的水，不监督”区域。监督在这个区域处于最低水平，而且无论C的增加有多大，监督都不会减少了。尽管这个模型非常简单，但是通过分析以上对C的增加所做的均衡行为回应，我们可以说明，与直觉相比而言，人们的回应实际上是多么的复杂与微妙。^[7]

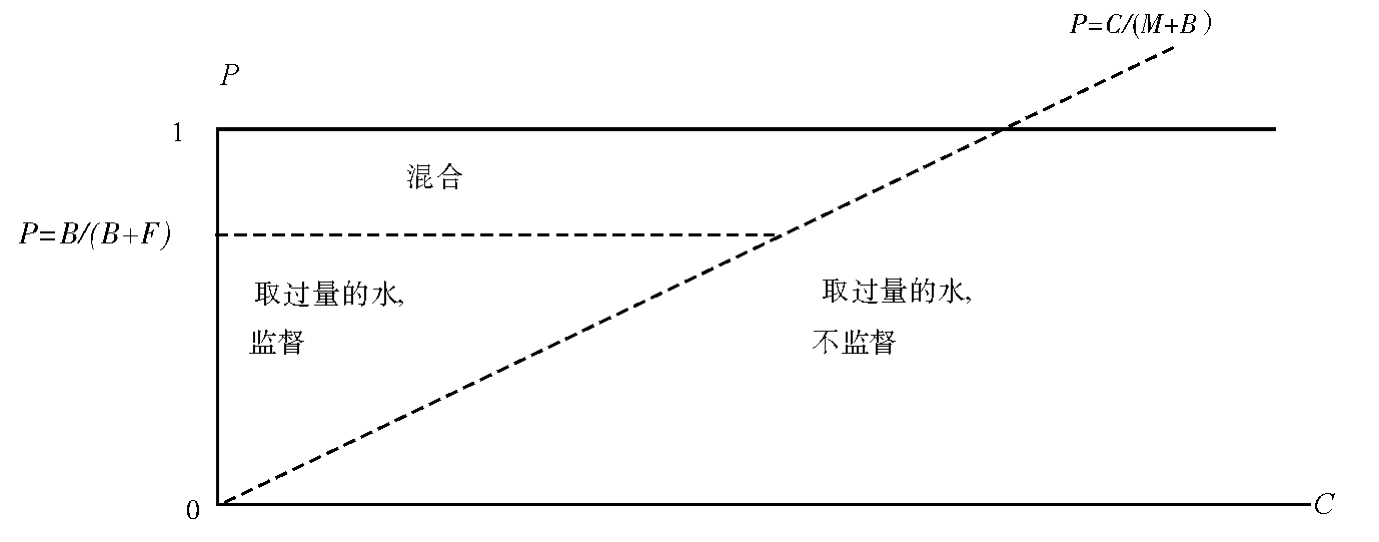
图3.10　监督的政区示意图

即使是在变量的变化将带来非常明确的定性效果的情况下，有关这种影响的更具体信息也经常是我们希望获得的。假设我们在考察一个由灌溉者组成的社群，他们目前面临的问题是如何减少偷窃。进行监督的农民的侦察效率上升、对欺诈者施以更严厉的惩罚以及雇用外部看护者，这些看起来都是降低偷水动机的合理手段。然而，哪种设计最有效果?如果不在相关变量构成的复杂系统内对实现目标的成本与收益进行分析和比较，我们就给不出这个问题的答案。^[8]