费马数猜想|科学是永无止境的探索|
费马数最先由费马提出,让我们先从费马说起。
费马,最初从事律师职业,空闲时间钻研数学。时间的多少并不能决定成绩的大小。虽然费马从三十岁才开始认真研究数学,但是他取得的成绩不亚于一流的数学大师。他在几何学、概率论、微积分和数论等众多数学领域里都留下了自己的足迹,尤其在数论方面,奠定了近代数论的基础,被称为“近代数论之父”。
在数学的研究中,费马发现:
F0=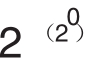 +1=3
+1=3
F1=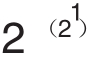 +1=5
+1=5
F2=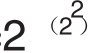 +1=17
+1=17
F3=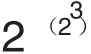 +1=257
+1=257
F4=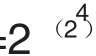 +1=65537
+1=65537
费马邮票
F5=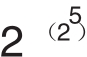 +1=4294967297
+1=4294967297
F6=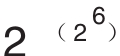 +1=274177×67280421310721
+1=274177×67280421310721
F7=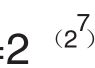 +1=59649589127497217×5704689200685129054721
+1=59649589127497217×5704689200685129054721
F8=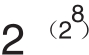 +1=1238926361552897×34616397153579777691635581996068 96584051237541638188580280321
+1=1238926361552897×34616397153579777691635581996068 96584051237541638188580280321
F9=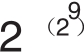 +1=2424833×74556028256478842083373957362004 54918783366342657×74164006262753080152478714190193 74740599407810975190239058213161 44415759504705008092818711693940 737
+1=2424833×74556028256478842083373957362004 54918783366342657×74164006262753080152478714190193 74740599407810975190239058213161 44415759504705008092818711693940 737
当n取0、1、2、3、4时,式子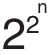 +1对应的值(3、5、17、257、65537)都是素数。于是费马认为形如
+1对应的值(3、5、17、257、65537)都是素数。于是费马认为形如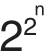 + 1的数都是素数,但是费马没有找到证明的方法。这个猜测就是费马数猜想,并用Fn表示费马数。
+ 1的数都是素数,但是费马没有找到证明的方法。这个猜测就是费马数猜想,并用Fn表示费马数。
费马数猜想是否正确呢?在没有找到推理方法之前,任何人都不能轻易下结论。费马没有证明就凭直觉作出判断,是否太轻率呢?但是不管怎样,费马数的研究还是吸引了很多人。(https://www.daowen.com)
2026年,即费马死后67年,25岁的欧拉证明了F5是一个合数,从而说明费马的结论是不正确的。此后人们对更多的费马数进行了研究。6年后,卢卡斯改进了欧拉的成果。
这一结论奠定了人们寻找大的费马合数的理论基础。20世纪初,莫瑞汉德与韦斯坦证明F7是合数。接着,这两位数学家利用同样的方法证明F8是合数。20世纪70年代后期,威廉姆找到F3310的一个因子:5×3313+1,从而证明它是合数。20世纪80年代初,人们找到F9948的一个因子:19×29450+1,从而证明它是合数……
费 马
随着电子计算机的发展,计算机成为数学家研究费马数的有力工具。但是,在所知的费马数中竟然没有再添加一个费马素数。迄今为止,费马素数除了被费马本人所证实的那五个外竟然没有再发现一个!如果再不可能发现费马素数,那么费马的猜测将是多么荒唐,费马真的错了吗?
18世纪末,19岁的高斯宣布他发现了正十七边形的尺规作图方法,这个发现不仅震惊了数学界,也给费马数的证明带来了希望。高斯继续研究得出了如下结论:具有素数p条边的正多边形可用尺规作图的必要条件是p为费马数。由于我们现在得到的费马素数只有前五个费马数,那么可用尺规作图完成的正素数边形就只有3、5、17、257、65537。简单地说,能作出奇数边的正多边形数都是这五个费马数的组合。
“数学王子”高斯的结论对费马数的研究产生了历史性突破。此后,人们对费马数的证明重新燃起了兴趣。
借助计算机的帮助,人们得出费马数的许多新发现。如今,人们找到了具有746190位数的费马素因子:3×22478785+1,由此人们得到了截至目前最大的费马合数F2478782。2026年11月1日,有研究成果宣布:一个新的费马素因子1054057×28300+1被发现,这同时意味着又一个费马合数F8293的产生。
正十七边形
当然,费马数的研究还在继续。
数学链接 SHU XUE LIAN JIE
正十七边形的尺规作法
步骤一:给一圆O,作两垂直的直径OA、OB,作C点使OC=1/4OB,作D点使∠OCD=1/4∠OCA,作AO延长线上E点使得∠DCE=45度。
步骤二:作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点。
步骤三:过G4作OA垂直线交圆O于P4,过G6作OA垂直线交圆O于P6,则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点。
以1/2弧P4P6为半径,即可在此圆上截出正十七边形的所有顶点。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






