复数的历史|揭去复数的神秘面纱|

根据我们的切身经历，我们知道，在实数范围内，对于有些运算仍然无能为力，只有把实数集扩充到复数集才能解决这一难题。可是，历史上引进虚数，把实数集扩充到复数集可不是件很容易的事，那么，历史上是如何引进虚数的呢？

16世纪意大利米兰学者卡尔达诺在1545年发表的《重要的艺术》一书中，公布了三次方程的一般解法，被后人称之为“卡当公式”。他是第一个把负数的平方根写到公式中的数学家，并且在讨论是否可能把10分成两部分，使它们的乘积等于40时，他把答案写成=40，尽管他认为这两个表示式是没有意义的、想象的、虚无缥缈的，但他还是把10分成了两部分，并使它们的乘积等于40。给出“虚数”这一名称的是法国数学家笛卡尔，他在《几何学》中使“虚的数”与“实的数”相对应，从此，虚数才开始广泛地流传开来。而至此，数系中发现一颗新星——虚数，于是引起了数学界的一片困惑。由于虚数闯入数的领域时，人们对它的实际用处一无所知，在实际生活中似乎也没有用复数来表达的量，因此，在很长的一段时间里，人们对虚数产生过种种怀疑和误解。笛卡尔称“虚数”的本意是指它是假的；莱布尼茨在公元18世纪初则认为：“虚数是美妙而奇异的神灵隐蔽所，它几乎是既存在又不存在的两栖物。”欧拉尽管在许多地方用了虚数，但又说一切形如（-1）、（-2）的数学式都是不可能有的，纯属虚幻的。

几何图解复数

1777年瑞士数学家欧拉开始使用符号i=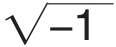表示虚数的单位。“虚数”实际上不是想象出来的，而它是确实存在的。虚数的出现，使无理数在有理数面前更加有底气，并且在虚数的基础上还引出了复数的概念，虚数其实很复杂，它的神秘面纱还没有被完全揭开，它在等待人们对它进行进一步的研究。虚数的名字来源于人们的“顽固”，好在现在人们对虚数的应用不那么糊涂了，人们已经懂得了它的重要性。之后，后人将虚数和实数有机地结合起来，写成a+bi形式（a、b为实数），称为复数。挪威的测量学家成塞尔在1779年试图给予这种虚数以直观的几何解释，并首先发表其做法，然而没有得到学术界的重视。德国数学家阿甘得在1806年公布了虚数的图像表示法，即所有实数能用一条数轴表示，同样，虚数也能用一个平面上的点来表示。在直角坐标系中，横轴上取对应实数a的点A，纵轴上取对应实数b的点B，并过这两点引平行于坐标轴的直线，它们的交点C就表示复数a＋bi。像这样，由各点都对应复数的平面叫做“复平面”，后来又称“阿甘得平面”。高斯在1831年，用实数组（a，b）代表复数，并建立了复数的某些运算，使得复数的某些运算也像实数一样地“代数化”。他又在1832年将表示平面上同一点的两种不同方法——直角坐标法和极坐标法加以综合，统一于表示同一复数的代数式和三角式两种形式中，并把数轴上的点与实数一一对应，扩展为平面上的点与复数一一对应。高斯不仅把复数看作平面上的点，而且还看作是一种向量，并利用复数与向量之间一一对应的关系，阐述了复数的几何加法与乘法。至此，复数理论才比较完整和系统地建立起来了。复数的乘、除、乘方、开方可以按照幂的运算法则进行。复数集不同于实数集的几个特点是：开方运算永远可行；一元n次复数方程总有n个根（重根按重数计）；复数不能建立大小顺序。

卡尔达诺

经过许多数学家长期不懈的努力，深刻探讨并发展了复数理论，才使得在数学地领域游荡了近200年的幽灵——虚数，揭去了神秘的面纱，显现出它的本来面目，原来虚数不虚。虚数成为了数系大家庭中的一员，从而才使实数集扩充到了复数集。复数的应用十分广泛。在系统分析中，系统常常通过拉普拉斯变换从时域变换到频域。因此可在复平面上分析系统的极点和零点。分析系统稳定性的根轨迹法、奈奎斯特图法和尼科尔斯图法都是在复平面上进行的。无论系统极点和零点在左半平面还是右半平面，根轨迹法都很重要。如果系统极点位于右半平面，则因果系统不稳定；都位于左半平面，则因果系统稳定；位于虚轴上，则系统为临界稳定的。如果系统的全部零点都位于右半平面，则这是个最小相位系统。如果系统的极点和零点关于虚轴对称，则这是全通系统。在应用层面，复分析常用以计算某些实值的反常函数，借由复值函数得出。实际应用中，求解给定差分方程模型的系统，通常首先找出线性差分方程对应的特征方程的所有复特征根r，再将系统以形为f（t）=e的基函数的线性组合表示。复函数于流体力学中可描述二维势流。一些碎形如曼德勃罗集合和茹利亚集是建基于复平面上的点……(www.daowen.com)

希尔伯特

随着科学和技术的发展进步，复数理论已越来越显出它的重要性，它不但对于数学本身的发展有着极其重要的意义，而且为证明机翼上升力的基本定理起到了不可估量的作用，并且在解决堤坝渗水的问题中显示了它的威力，而且还为建立巨大水电站提供了重要的理论依据。

数学链接 SHU XUE LIAN JIE

希尔伯特空间

在数学领域，希尔伯特空间是欧几里得空间的一个推广，使其不再局限于有限维的情形。与欧几里得空间相仿，希尔伯特空间也是一个内积空间，其上有距离和角的概念（及由此引申而来的正交性与垂直性的概念）。此外，希尔伯特空间还是一个完备的空间，其上所有的柯西列等价于收敛列，从而微积分中的大部分概念都可以无障碍地推广到希尔伯特空间中。希尔伯特空间为基于任意正交系上的多项式表示的傅立叶级数和傅立叶变换提供了一种有效的表述方式，而这也是泛函分析的核心概念之一。一个抽象的希尔伯特空间中的元素往往被称为向量。在实际应用中，它可能代表了一列复数或是一个函数。例如在量子力学中，一个物理系统可以表示为一个复希尔伯特空间，其中的向量是描述系统可能状态的波函数。