在前面讨论分工和专业化的含义时，我们指出，斯密和斯蒂格勒均注意到交通运输发展在分工和专业化中的作用。正如杨小凯的观点，分工和交易成本之间存在两难冲突，分工会带来专业化效益，同时也会造成交易费用增加。只有分工带来的专业化效益超过增加的交易费用时，分工才会继续演进；否则，分工会停滞不前。空间交易成本的一个重要组成部分就是运输成本以及由空间距离所带来的空间成本，交通运输业发展会带来可达性的提高和运输成本的降低，从而降低交易成本和空间成本，进而促进分工和专业化的发展。

按照古典经济学的分工理论，分工与市场规模之间存在一种相互促进的关系，按照杨小凯和张永生[1]将杨格思想总结为“杨格定理”的说法，不但市场的大小决定分工程度，而且市场大小受分工程度的制约，分工的演进具有自组织的特征：

市场规模扩大→专业化分工↑→市场规模继续扩大→专业化分工↑

一般来说，影响市场规模的因素有三个：市场的地理范围、人口数量和人均收入。人口数量增长意味着潜在交易主体的增加，而人均收入是购买力的基础，因此简单来看，这两者与市场容量之间是一种正相关关系。但是，盛洪认为，这两个因素对市场容量的影响不具有突破性意义。因为人口数量和人均收入之间是一对相互制衡的因素，经常是相互反向变动的[2]。当总量一定时，人口增长带来人均收入的下降，进而影响购买力；而人均收入的下降带来人口增长的停滞，于是又会使人均收入增长。除非经济总量增长高速于人口增长（这在社会分工最初产生的前现代社会并不一定成立），否则人口数量和人均收入对市场容量的影响将是相互抵消的。所以，作为分工产生前提的市场容量的扩张，主要归因于市场范围的扩大。就此，我们可以推导出这样的命题：城市群内产业分工作为社会分工的空间形式，其形成须以区域（乃至全国）统一市场的建立和不断扩大，进而市场容量足够大为前提。

那么接下来需要考虑的是，区域统一市场的地理范围究竟能有多大，以及哪些因素影响其地理范围的问题。我们将构建一个基于新古典区位论和新制度经济学思想的模型加以解释。

图6.1　城市A某产业（产品）的区域市场范围

如图6.1所示，假定某城市群区域O是半径为x+y+z的均质圆形区域，群内人口密度、居民购买力及运输条件均相同。群内某城市A（以点A表示）某基础部门制成品的行业平均成本曲线为AC，区域O内消费者对该类制成品的需求曲线为D，城市A该制成品生产企业（或行业联合体）依据平均成本定价原则，将平均收益（FOB价格）定为P。由于是基础部门，该类制成品主要输出到城市A以外的地区，市内销售忽略不计。在对外销售中，需考虑运输费用和交易费用。这样一来，产品对外销售的有效价格（CIF价格+交易费用）P′=P+t+t′表现为一条向上倾斜的曲线。这是因为，单位产品的运输成本和交易成本均随产销地之间距离的扩大而提高，其中，单位运输费用具有随运距增加而边际递减的特征；单位交易费用则正好相反，产销两地距离越远，生产企业为销售一单位产品所必须投入的与交易相关的资源就越多，包括广告、宣传、设立销售网点等多种费用的均摊。

P′与D曲线交于N点，这一点对应的产销量为Q2，价格为P2，投影在区域O上的产销地距离为x+y。在运输条件均质的前提下，以城市A为圆心、x+y为半径的圆为城市A生产的该类制成品在区域O的市场范围的上边界。在此区域市场范围以外，由于有效价格过高，区域O中已不再有需求。另外，产品销售和区域市场的形成还必须满足企业的获利要求，即市场范围要大到足以使企业盈亏平衡。在图6.1中，P′与AC的交点M即为盈亏平衡点，以A为圆心、M点对应的产销距离x为半径的圆即构成城市A生产该类产品的区域市场范围的下边界。在此边界以内，由于平均成本过高，甚至高于其有效价格，企业因无法盈利将放弃生产。

理论上讲，该类产品区域市场的实际边界将位于上边界和下边界之间，其具体位置受市场结构、生产能力，甚至偶发事件等多种因素的影响。

根据该模型可知，影响区域统一市场范围的因素包括供给和需求两方面。供给方面主要涉及各种成本因素，包括交易成本、运输费用和生产成本，成本因素对区域市场范围的扩大起制约作用。此外，供给能力、市场结构、企业区位、竞争行为等也将产生种种影响。需求方面的因素则主要包括城市群内居民的购买力水平和消费偏好，这两个因素直接决定了需求曲线的位置和形状。

我们也可以用数学模型来描述交通运输对市场需求的影响。为了简化，我们假定企业生产单一的产品供应单一的顾客，此人的居住地在离企业事先确定的地点有一段距离，因此，商品要满足消费者的需求，必须克服空间距离的障碍，即会产生运输成本，假定运输成本由供应者负担。因此我们可以得到：

其中：Ps是商品的供给价格；Pd是商品的需求价格；Qs是商品的供应量；Qd是商品的需求量；pt是运至顾客手中的每单位商品的不变运输成本。

根据上述方程，我们可以求得利润最大化的供应量Q*：

从（6.5）式我们可以看出，随着运输成本的提高，由供求决定的均衡产量会下降。为了和现实更相符合，我们也可以对消费者在空间上的分布作出其他描述，但是，结论都是一样的，即：运输成本是决定企业服务市场地域规模的关键因素。运输成本越低，市场规模越大；运输成本越高，市场规模越小。

交通运输发展会带来市场规模扩大，市场规模扩大则会促进分工，分工则会产生专业化经济，但是分工同样会带来交易数量和频率的增加，从而造成交易成本的增加。那么，最优的分工度则是在分工带来的专业化经济和交易成本增加之间的权衡。

用单位运输成本描述交通发展程度，用分工度定量测度社会分工程度，则可以通过分工度与单位运输成本之间的数理关系，表述交通发展与社会分工之间的关系。

设经济系统中的市场属于“纳什议价均衡”，即交易费用仅为外生交易费用（主要包括流通费用等），设在T分工方案下，在一定的交通条件时分工度为f，经济系统中经济流数量为M，则[4]：

式中：M为经济系统中的经济流量数，f为分工度。可得：

假设经济系统中每对协作关系的流量均为物资流量，每个物资流量大小为q，系统中的总流量为：

设系统中实行无歧视定价，且单位运输产品运价（即运价率）与单位运输成本具有简单线性关系，如每单位运输成本为u，运价率为：

T=ku

式中：k为参数，且k＞1。

系统中物资流量的平均运距为d，则系统中总的流通费用为：

在分工度f下，系统总生产费用为f的函数：

式中：α、β为大于零的参数。

为简单计算，取β为1，此时，生产费用函数为：

只有当分工度增加的流通费用小于提高分工度减少的生产费用时，分工才会演进。当提高分工度增加的流通费用等于提高分工度减少的生产费用时，分工度达到最佳经济效果，即：

满足（6.12）式条件的分工度称为最佳分工度，用f*表示，则：

求解（6.13）式，可得最佳分工度f*：

（6.14）式描述了最佳分工度f*和单位运输成本u之间的关系，由此可见，最佳分工度f*是单位运输成本的减函数，即单位运输成本降低，最佳分工度增大，说明社会分工水平提高引起的边际经济增长率大于边际交易费用，分工向前演进。

以上我们从理论上证明了交通运输发展与分工之间的正相关关系，美国从19世纪初到南北战争爆发之前，中西部地区交通运输业的发展对农业、工业的影响更直观地说明了上述理论[5]。

19世纪初该地区的道路条件差，公路运输价格昂贵，农产品的运输费用制约了成交量、交换范围、交换价格，严重影响农业生产的规模，但从1848年起，中西部以北地区铁路运营里程数大幅增加，交通运输条件逐步改善，运输成本降低，这不仅给农民更大盈利空间，提高农民收入，而且使得消费者能够以更低的价格购买所需农产品，引起消费者对农产品需求的增加。这些铁路的建成沟通了东西部的经济联系，形成了全国性的统一市场，为西部大草原的畜牧业产品提供了广阔的国内市场。铁路的发展降低了货物的运输成本，高效的运输体系完成了对大量原料、中间产品和最终产品的运送工作，加强了直接生产部门内部的交换合作，使生产者之间交换商品的数目急剧增加，使得大规模生产成为可能，进一步降低生产成本，鼓励分工发展。这一时期稳定可靠的交通运输能力保证了Ohio，Indiana，Michigan等几个州的农产品在美国东部地区市场上的销售。随着中西部地区农业生产逐渐扩大，与农产品加工相关的行业在该地区越发重要，包括面粉业、皮革业、肉制品包装业等，例如在1840年，大西洋中部一些州所生产的面粉量占总产量的65%，而到了1860年，这一比例仅为39%。肉制品包装行业亦如此，1860年芝加哥猪肉包装业的收入是1852年的3倍，牛肉加工业的收入是1852年的2倍。同时，农产品加工相关的行业因自身的特点为新行业创造了市场需求，比如，面粉行业需要大量的机器设备投入，1860年该行业的单位产出所需资本量在所有行业中排第四，资本—产出率几乎是制造业的2倍。高资本—产出率鼓励了对蒸汽动力的使用，对蒸汽动力的使用又加大了对机器设备及生产工具等产品的需求，导致最终美国机床业的发展，而与此同时，农产品加工行业中的工人劳动生产率也已提高为从前的2倍还多。另外，先进的科学技术在国内的广泛传播和应用减缓了产业结构向更高级阶段过渡的过程中的压力，由于产业间的关联作用，整个经济体系当中便形成了一种无休止的产品供给和需求的“连锁反应”，使得市场规模扩大、产出水平提高、分工进一步深化，通过循环累积的过程实现经济增长。

区域分工和专业化的形成实际上是通过区域产业结构调整来实现的，产业结构调整又是通过新企业的定位选择和既定企业的重新定位这一动态过程来实现的。产业结构调整是一个复杂适应系统，它受到包括企业、地方政府、中央政府等主体以及环境等的影响和作用。我们主要分析交通运输对区域产业结构的影响，因此，假设经济和社会环境的变化对各地区及其企业的影响是普遍和平衡的。这样我们就可以将区域间产业结构调整进而区域间分工和专业化形成，看做是各区域的企业对交通条件的变化作出反应而自发演进的结果。

两个相邻地区间既定企业的重新定位问题可以近视地看做既定空间买卖双方垄断厂商的空间博弈问题。我们可以借助霍特林模型[6]来说明交通运输的改进对区域产业结构调整的影响。

假设两个位于既定区位的厂商1和厂商2销售相同产品，分布在长度为l的线段上，离线段端点的距离分别为a和b（a+b≤l），他们在价格上相互竞争以吸引分散在空间的消费者。运输成本是距离的线性函数，令t为运费率。消费者沿直线均匀分布；不失一般性，设密度为1。每个消费者只购买一个单位的产品，不管其价格如何。由于产品是同质的，消费者将惠顾总价格更低的销售商。令p1、p2分别是厂商1、2设定的出厂价格，为了说明交通运输对产业结构调整的影响，我们假设厂商1所在的区位具有生产该产品的相对优势，即p1＜p2，那么我们可以发现：

1）如果P1＜P2-t（l-a-b）那么所有消费者都会购买厂商1的产品，厂商2的产量为0，也就是说此时只有区位1会生产该产品。

2）如果P2-t（l-a-b）≤P1那么市场边界位于两个厂商总价格相等的一点，对厂商1来说，该边界的距离为R=［（P2-P1）+t（l-a-b）］/2t

（6.15）

从（6.15）式我们可以得到

由于P1＜P2，所以，也就是说随着交通成本的下降，厂商1的市场边界越来越大，直到P1＜P2-t（l-a-b）时，全部市场为厂商1所占领。

从以上对霍特林模型的简单讨论我们可以知道，随着交通运输条件的改善，价格较低的厂商的生产规模将逐步扩张，而价格较高的厂商将逐步被驱赶出市场。

将同样的分析方法应用到两地区同一产业竞争的分析中，我们可以得到同样的结论：原先对某一产业具有相对优势的区域，随着交通运输的改善，其在该产业的相对优势会逐步扩大，生产规模也逐步扩张，而原先处于劣势的区域将被逐步赶出该产业的生产。

至于两个以上地区间既定企业重新定位问题，我们可以近视地将其看成垄断寡头条件下多个厂商的空间博弈问题。格林哈特等通过对厂商需求函数和市场均衡的分析发现，厂商的市场需求函数仅仅与相邻厂商的价格有关，而与更加远的厂商的价格无关，这意味着需求呈链状结构，每个生产者直接与它相邻的生产者进行竞争，而不必考虑相离的生产厂商。因此，在考虑交通条件变化与各地区工业结构调整问题时，主要是考虑相邻地区。

将以上结论用于分析交通运输对城市群城市间分工、专业化的影响，我们可以得到如下结论：①随着交通运输的发展，各城市间的分工、专业化程度越深；②交通运输对相邻城市的分工专业化的影响大于相离城市的影响。

以上部分我们仅仅说明了交通运输的发展会促进区域分工和专业化的发展，但是，对于具体如何分工则没有涉及，只是说明了原来具有相对优势的产业将随运输成本的下降进一步得到加强。本部分主要从理论上说明不同运输成本的产业在空间上的分布[7]。

6.2.2.1　模型

假设有两个对称区域，H，F，K（K≥2）类产业和三种物品，即初始禀赋同质商品（它也被选作是记账单位）、用规模报酬递增技术生产的差异化产品以及土地。每类产业中有Nk种异质产品，假设每个企业只能生产一种产品，因此每类产业中都有Nk个企业，这些企业都服从规模报酬递增。假设工人不能在产业间流动，但是，工人可以在区域间自由流动，即认为工人在区域间流动的成本为0。

除了企业要用地以外，工人住房也需要用地。并且假设每个地区都有CBD，这个区域的所有企业都位于CBD，空间围绕CBD线性分布，每一区位有一单位土地。每个工人住房消费一单位土地，工人上下班往返CBD，假设每单位距离的往返交通成本是θ，土地的机会成本是0，整个区域的土地租金平均分配给区域的所有居民。在上面假设下，每个工人的净城市成本（它等于土地租金支出+往返交通成本-土地租金收入）是×区域人口，这和工人的区位不相关。

根据Tabuchi和Thisse（2003）[8]的分析框架，假设工人有相同偏好，效用函数为：

q0代表同质商品的消费数量，qi（j）代表第i类产业第j种商品的消费量。我们假设α＞0，β＞γ＞0，这也意味着工人偏好多种消费，从（6.17）式的第二项可以看出，具有更多企业的产业比具有更少企业的产业对工人的效用影响更大。

每个工人的收入预算约束为：

其中：pir（j）、qir（j）分别是区域r的工人消费第i类产业第j种产品的价格和数量，Lir是区域r第i类产业工人的数量，wir是区域r第i类产业工人的工资。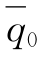是初始赋予的同质商品数量，假设它足够大，使均衡消费q0为正。

由工人的效用最大化，可以得到需求函数和直接效用函数Vir：

其中：a=α/β，b=1/（β-γ），c=γ/［β（β-γ）］，Pi是区域r第i产业的价格指数。由于β＞γ＞0，因此我们有b＞c＞0。

由于需求函数是价格的线性函数，不同产业价格的系数是不同的，因此，企业越多的产业，它的需求价格弹性越小。

每个企业都以垄断竞争的方式生产差异化产品。假设每个企业都是足够小，它的价格对价格指数几乎没什么影响。同样假设所有产业都能用一单位劳动生产一单位的差异化产品，因此有Ni=Li。不同产业的跨区域产品运输成本是不同的，第i产业的一单位产品运输成本为τi。在上述假设下，在同一区域同一产业内的企业都是对称的。区域r第i产业的典型企业最大化利润为：

其中：qirs、pirs分别是位于区域r的第i产业的企业在区域s的需求和价格。

在最大化利润为0以及自由进入的假设下，可以得到均衡价格和工资：

从上述方程，可以得到不同区域的产业i的工人的效用差为：

其中：Sr是区域r的消费者剩余，λi是产业i居住在H区域的工人的比例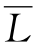，是工人总数。

另外，为了简化，假设τi=ωiτ，θ=ρτ，这也意味着随着τ下降，运输成本和通勤成本分别按一定比例下降，这个假设比较严格，但是，可以使我们只用一个参数τ来描述技术进步。

在这些假设下，效用差（ViH-ViF）可以重新写成：

其中：

最后，可以用下述动态系统来描述区域间的迁移行为：

6.2.2.2　基于交通技术进步的区域专业化

现在我们再来看看当交通技术进步、运输成本和通勤费用降低时，产业区位是如何变化的。我们可以看见产业区位的变化将取决于交通成本与产业规模的比例（ωi/Li），我们将该比例称为调整交通成本。为了简化，我们采用以下三条技术性假定：

1）任何两个产业的调整交通成本都是不一样的，即：

2）产业不能划分为具有相同工人的两类。即1，…，l，…，K类产业中的任何一种排列i1，…，il，…，ik，都有：

对K类产业的任何划分｛1｝，｛i1，…，il1｝和｛j1，…，jl2｝（l1≥0，l2≥0，l1+l2=K-1），都有：

上述假设比较严格，把参数空间中测度为0的参数排除了。不失一般性，产业按下列顺序排列：

我们可以得到以下定理：(www.daowen.com)

定理1：如果τ足够小，最多只有一个产业扩散。

证明：我们以下证明，对于足够小的τ，任何一种k（≥2）类产业扩散的配置都是不稳定的。采用反证法。

假设一种有k类产业扩散的稳定均衡。把扩散产业用1，…，k表示，定义

δij如前面定义，考虑与动态系统相关的均衡稳定性，-Δ的特征根的实数部分一定小于0，因此，可以得到|Δ|＞0。

设定：

（Θi，Υ-i）是矩阵Υ的第i列由Θi代替，其他元素不变形成的矩阵。由于v2=μ2+ξ2，它服从

其中：第一项是τ的2k阶多项式，第二项是τ的2k-1阶多项式。我们可以证明多项式中2k-2阶以下的项系数为0，因此，多项式中2k-2阶这项非常重要。我们可以证明|Υ|的2k-2阶项为负，的2k-2阶项为0。因此，当τ足够小时，|Δ|＜0。

和前面|Δ|＞0相矛盾，因此证明了不可能有两种以上产业同时扩散。

这个定理也告诉我们，如果τ足够小，只有以下两种区位模式是可能的：一种是每一类产业都集聚在其中一个区域；另一种是只有一类产业是扩散的，其他产业都是集聚的。

在前面假设两个区域是对称的，为了区分区位模型，我们假设H区域的人口大于等于区域F的人口，对i，l=1，…，K，设定：

函数ρ†（i，l）有以下性质：

引理1：1）ρ†（i，l）是i的严格单调减函数，即ρ†（i，l）＞ρ†（i+1，l），对i=1，…，K-1。

2）如果，则ρ†（i，l）对任意i都是正的。

3）如果，则ρ†（l，l）＜ρ†（l，l-1）。

上述引理的证明比较简单，此处从略。

为了简单，我们假设ρ≠ρ†（l，l），ρ†（l+1，l），对l=l#，…，K

为了方便，我们定义ρ†（K+1，K）=0，采用这种方法，我们把参数空间中测度为0的参数排除。

下边的引理给出了每一类产业都集聚在其中一个区域以及只有一类产业是扩散的，其他产业都是集聚的稳定条件。

引理2：对一个足够小的τ，如果有一类产业l≥l#使产业1，…，l集聚在H区域，产业l+1，…，K集聚在F区域，并且使得ρ†（l，l）＞ρ＞ρ†（l+1，l），那么每一类产业都是集聚的均衡是稳定的。

引理3：对足够小的τ，如果有一类产业l≥l#使产业1，…，l-1集聚在H区域，产业l+1，…，K集聚在F区域，并且，那么，只有一类产业是扩散的均衡是稳定的。

上述引理有以下隐含含义：第一，对足够小的τ，具有大的调整运输成本的产业和具有小的调整运输成本的产业的区位是分离的，也就是说，基于调整运输成本的区域专业化出现。第二，具有大的调整运输成本的产业位于人口数量较大的地区。第三，扩散产业l由通勤费用与运输成本的相对大小即ρ决定。

从以上的分析我们可以看出，随着交通运输技术的进步，不同区域间将会出现专业化，同一种产业将呈现集聚分布的状态，而且运输成本与产业规模比例比较大的产业将集中在人口数量比较大的地区，也就是市场规模比较大的地区。当然，以上的讨论均没有考虑如集聚产生的知识溢出效应等，仅仅是考虑了交通运输成本。

城市群是城市集团式发展战略的空间表现形式，是由核心城市及其周边城市和地域共同组成的紧密联系的一体化区域。城市群体是一个高密度、关联紧密的城市空间，城市群本质上是个区域一体化的概念。在经济全球化背景下，各国各地区的经济由彼此孤立走向联系和依赖，这是生产社会化发展的客观要求。在经济全球化背景下，各类生产要素的远距离高度整合成为现实。在一国范围内，则表现为以城市群的形成为标志的区域经济一体化，这是区域经济发展的必然趋势。在经济全球化背景下，城市间的竞争不再单纯地存在于城市之间，城市的竞争更多地表现为区域竞争或集团竞争，这也是世界上很多大的城市群出现的重要原因之一。在城市群内，各城市从自身比较优势和竞争力出发，通过竞争实现整合，逐步形成以分工协作为基础的区域性城市网络、产业网络，进而逐步形成整体优势与竞争力，是各城市参与全球竞争应采取的发展战略。

交通运输是实现城市间物质、能量交换的载体，发达的交通设施是实现城市间合理分工和经济一体化的必要条件。一个成熟的城市群不仅内部有发达的铁路、公路、水运和通讯网络将大小城市连为一体，而且城市群还通过现代化的海港、国际航空港与其他地区发生密切联系，参与国际分工。

按照新经济地理学的理论，运输成本不但是市场一体化的反义，而且对地区专业化、产业集聚来说始终是外生的。报酬递增与运输成本结合起来，制造业厂商总是选择最接近于大市场的空间某一点进行制成品生产，当许多厂商都抱有相同的决策时，“空间外部性”或称“产业集聚的正外部性”就被创造出来了。在这种情况下，由运输成本引起的产业集聚向心力导致一个具有初步制造业优势的地区可以通过累积循环机制将这一优势逐渐放大和巩固，直到别的地区制造业逐渐消失，这时产业分布就呈现出“制造业中心—农业外围”格局。几乎所有的产业都集中在制造业中心地带，这一地区的产业平均集中率、地区间专业化指数与地区相对专业化指数都处于极高的水平。因此，伴随着运输成本的最初降低，地区的产业集聚现象发生，极化效应开始显现。

随着交通运输的进一步发展，运输成本进一步降低，地区的产业集聚状况将发生显著变化，此时极化效应弱化和扩散效应开始显现。因为在这一情况下，产业集聚到一定程度后产生的地区内非贸易品价格高企不下、环境污染等拥挤成本往往超过了引向集聚的向心力，部分技术含量低、劳动密集型产业将不得不率先从原制造业中心向周边地区转移，而原制造业中心可能会衰落，或者发展成为技术或资本密集型产业中心，或者纯粹成为技术创新、贸易、金融服务等中心。因此，可以想象此时地区之间开始实现产业梯度转移和分工协作。

如果交通运输业进一步发展，制度进一步完善，城市群的一体化水平推进到很高的水平，由于制造业规模报酬递增特性，某一产业将集中在一个地区生产来满足其他地区对该产品的需求，相应地，别的地区也专注于另一种产品的生产，各地区都实现了有差异的产品生产，从而出现了近似的地区完全专业化，此时单个产业的集中度与地区专业化都处于很高的水平。

综上所述，我们可以总结出交通运输与城市群分工和专业化发展水平演化之间的关系：

在城市群发展的初始阶段，由于交通运输极不发达，此时各城市之间各自独立发展，城市间的联系很少，没有形成专业化的分工合作，城市间的分工水平极低；在交通运输发展到一定程度之后，各城市之间发现专业化带来的规模报酬递增能弥补分工带来的包括运输成本在内的交易成本的增加，此时，由于制造业刚处于起步阶段，通过循环累积机制的作用，部分具有区位优势的城市将成为产业集聚地，城市群内的分工专业化水平很高；当城市群的交通等推动的一体化推向高级阶段时，由于产业集聚的拥挤效应的出现，此时制造业会开始出现梯度转移和分工协作，但此时的城市间的分工、专业化水平会下降；随着交通运输业的进一步发展以及制度的完善，城市群的一体化水平会达到很高程度，此时城市群内各城市之间的职能分工比较明确，各城市都会基于自身的优势专注于少数产品的生产，此时城市群的专业化分工水平会进一步发展，值得注意的是，此时的分工有可能是产业内分工，如果以产业部门的产值或就业来度量分工水平，则反而从数值上表现为分工水平下降。

Kim[9]（1995），Gordon[10]（1998），Meyer[11]（1983）发现在美国地区经济发展史上，在一体化水平的前期阶段，即在19世纪末20世纪初，随着以铁路、运河为内容的交通运输建设的展开，美国制造业主要集中在东北地区、大西洋沿岸中部和以五大湖为中心的中西部地区，此时地区专业化水平处于较高水平；但随着一体化的更进一步推进，20世纪中期以后，美国制造业迅速向西部地区、南部地区扩散开来，专业化水平急速下降。

这些事实揭示了一个已被理论证明了的经验规则[12]（Fujita，Krugman and Venables；1999），即一体化水平从低级阶段向中级阶段挺进时，产业的地区集中率是上升的；而一体化从中级阶段向高级阶段挺进时，产业的地区集中率是下降的，即新经济地理学所谓的著名倒“U”字形曲线。

改革开放后，长江三角洲地区已成为中国经济增长中最有活力、增长潜力最大的地区，无论从经济规模、人口数量和质量还是从市场化和国际化等因素来衡量，长江三角洲地区已成为中国经济增长的发动机。我国正处于工业化中期阶段，工业化成为推动城市化和经济发展的主要动力。长江三角洲作为中国经济的龙头，在改革开放后，工业化飞速发展，工业地理集中现象明显。在1965～1978年期间，江苏省工业产值占全国的比重只上升了1.7个百分点，浙江省几乎没有发生变化，而上海下降了4个百分点，总体上江浙沪工业地位呈下降态势。1978年以后，江浙两省的工业地位急剧上升，到2003年江苏的工业比重上升为全国的12.68%，浙江上升到9.04%，上海的工业产值比重上升到7.27%。总之，江浙沪的工业占全国的比重从1978年的23.22%上升到2003年的28.99%，增加了近6个百分点，长江三角洲地区成为中国最大的制造业带。

长三角制造业带兴起的部分原因来源于连接该区域各城市的铁路干线及沿干线附近城市的公路网。交通网络本身就是制造业优势的一部分，制造企业在选择生产区位时必然考虑地区的市场和运输条件。一方面，如果固定成本相对于运输成本足够大，人口较多的地区将会吸引制造品的生产集中在该地区；另一方面，运输本身有规模经济，一条铁路线或一条公路代表一个不可分的投资，制造企业越是集中，区域内部之间的运输量就会大大高于其他线路上的运输量，意味着运输成本较低，这反过来强化了长江三角洲作为生产地区的优势。长三角地区不仅人口密集，运输网络也更为发达，制造商容易进入市场。因而，运输网络效应和当地市场规模效应在长三角制造业带的形成过程中是共同发挥作用的，市场规模的扩大是基于工业化程度提高和劳动力收入的较大幅度增长所带来的。应该说，劳动力收入增长比人口增长更重要，它使当地市场迅速扩大。

对于城市群来说，内部是否形成分工专业化，将决定城市群的竞争力。而对于长三角内部是否存在产业同构现象是一个尚未解决的问题。很多研究都认为长三角存在产业同构问题，城市之间的分工和专业化不显著。那么，长三角究竟存在怎样的分工、专业化模式，下面将进行深入研究。

有很多统计指标可以用来度量区域分工和专业化，如区位商、集中度、赫芬达尔指数、基尼指数等。我们这里用熵指数来度量分工、专业化。使用熵指数具有如下优点：首先，熵指数可以反映个别产业变动对整体产业变动的影响；其次，它是将各产业的变动加总得到整体产业的变动，而像集中度等指标就没有加总性的特征。

所谓地区专业化，就是“各个地区专门生产某种产品，有时是某一类产品甚至是产品的某一”[13]。地区专业化是对一个地区的专业化发展过程和专业化发展程度的描述。一个地区在某一时点上可能表现为极为专业化，如一个地区只有一个产业；也可能表现为完全多样化，如一个地区其所有产业的从业人员一样多，增加值的贡献一样多，产值一样多。当然这是两种极端现象，更多情况是某一个或某几个产业的从业人员占该地区从业人数的多数。我们可以用专业化熵指数来度量地区专业化程度：

其中：Xij表示j地区第i产业的产出，i=1，…，n，j=1，…，k；

表示j地区各产业产出之和；表示各地区第i产业产出之和。

从（6.38）式我们可以看出，如果一个地区极端多样化，每个产业的增加值都相等，那么对所有i都有Xij/Xj=1/n，从而专业化熵指数将SPEC= lnn；反之，如果一个地区极端专业化，地区只生产一种产品，那么SPEC= 0。通常，一个区域专业化程度越高，SPEC越趋向于0，也就是说，SPEC与专业化程度呈反相关关系。

产业的地理集中考察的是一个产业在不同地区的分布情况，即产业的空间分布，对于产业的地理集中度我们可以用以下公式表示：

和产业专业化熵指数类似，产业的地理集中熵指数位于0和lnk之间，并且指数值与产业的地理集中度呈反向变化，即地理集中度越高，CONCi越低。

为了得到整个区域或国家的产业分工专业化程度以及产业集中度，我们将上述得到的各地区专业化指数和产业集中度指数用加权平均数求和：

将（6.38）、（6.39）、（6.42）、（6.43）式代入（6.40）、（6.41）式我们可以得到：

为了计算长三角的分工与专业化程度，我们采用江苏、浙江以及上海三省市的24个制造业增加值来分析（资料来源于《中国工业统计年鉴》）。根据上面公式我们计算了长三角的三省市专业化熵指数，结果见表6.1。我们发现上海和江苏的熵指数都是在1994～2000年间逐步上升，而在2000年以后逐步下降；浙江则在1994～1997年间专业化指数逐年上升，在1997年后则逐年下降。由于熵指数是和分工、专业化水平呈反方向变化的，因此，上海和江苏的专业化水平在1994～2000年间是逐步下降，而在2000年后是逐步上升的；浙江则在1997年后专业化水平逐步上升。

表6.1　长三角地区间专业化指数变化

而从三省市的比较来看，上海的熵指数最小，浙江其次，而江苏最大，表明上海的专业化水平最高，浙江其次，而江苏最低。

这和长三角地区包括交通在内的一体化进程是相符的，从20世纪90年代后期开始，长三角城市群加大了交通运输业投资。尤其是沪宁高速公路、沪杭甬高速公路分别在90年代中后期建成通车，将长三角各城市更紧密地联系在一起，有力地促进了地区一体化以及分工、专业化的发展。我们可以预期，随着在2010年前江苏10座跨江通道、浙江杭州湾大桥和舟山跨海大桥的成功建设，杭甬、杭沪、杭宁、沪宁间的高速公路的扩建、再建，以及舟山连岛工程的建成，整个长三角的经济将形成更密切的分工合作关系，分工与专业化程度将进一步加深。

同时，我们也计算了集中指数，结果见表6.2。

表6.2　长三角产业地理集中指数

表6.2的数据表明，长三角产业地理集中趋势和产业分工、专业化的变化趋势基本一致，在2000年之前，产业的地理集中分布呈分散状态，在2000年之后，地理集中度开始有所提升。

上面我们只是得到了长三角地区分工、专业化发展趋势，为了进一步分析地区间产业结构差异我们采用下列公式：

其中：i、j、k分别为地区i、地区j、产业k，、分别为地区i、j产业k的增加值。

根据上面公式我们可以得到衡量制造业结构差异的各省市之间的专业化指数，结果如表6.3所示。

表6.3　长三角各省市之间的专业化指数变化趋势

从表6.3我们可以看出，江苏、浙江和上海之间的专业化指数表现出相同的发展趋势，即在2000年之前是逐年下降的，而在2000年之后是逐年上升。江苏和浙江之间的专业化指数则是逐年上升。

而从各省市之间的结构差异来看，上海和浙江之间的结构差异最大，江苏和上海的结构差异次之，而江苏和浙江的制造业结构最为雷同。通过这些数据我们可以得到如下结论：①浙江相对于江苏来说，随着长三角一体化的推进，它与上海更有效地实现了产业分工，浙江更专注于劳动密集型产业生产而上海更注重于资本技术密集型、港口型产业生产。②江苏与上海之间的专业化指数在2000年之前下降比较大，2000年之后虽有所提高，但是提高速度缓慢，说明江苏内部的主导产业与上海可能有重叠之处，即可能都偏向于重化工业，而不像浙江那样侧重于消费类轻工业。③江苏省的人口规模、制造业总体规模远远大于其他两个省市，它通过自给自足来满足自身需求的程度更高，这导致江苏省与其他两省市的制造业结构差异最低，特别是与同处于工业化起飞阶段的浙江省相比，制造业结构差异程度相对于地区间一体化水平、地理位置相邻等条件来说处于不相称的地位。

[1]杨小凯，张永生.新兴古典经济学与超边际分析.中国人民大学出版社，2000

[2]盛洪.分工与交易——一个一般理论及其对中国非专业化问题的应用分析.上海人民出版社，2006：140

[3]王花兰等.交通发展与社会分工关系模型研究.铁道运输与经济，第27卷第5期

[4]杨小凯.数理经济学基础.国防工业出版社，1985

[5]杨铁.从产业间分工角度谈交通运输对经济增长的作用.沿海企业与科技，2005（2）

[6]彼得•尼茨坎普主编，安虎森等译.区域与城市经济学手册（第1卷）.经济科学出版社，2001：34～39

[7]主要参考Hajime Takatsuka and Dao－Zhi Zeng.Regional Specilization via Differences in Transport Costs：An Economic Geography Approach.Graduate School of Management，Kagawa University，Working Paper Series

[8]Tabuchi，T.and J.F.Thisse，2003.Regional specialization，urban hierarchy and commuting costs，CORE Discussion Paper No.2003－60.http://www.core.ucl.ac.be/services/COREdp03.html

[9]Kim S.Expansion of Markets and the Geographic Distribution of Economic Activities：The Trends in U.S.Regional Manufacturing Structure，1860－1987.Quarterly Journal of Economics，Vol. 110，1995：881～908

[10]Gordon，P.，H.Richardson，and G.Yu.Metropolitan and Non－metropol -itan Employment Trends in the U.S.：Recent Evidence and Implications.Urban Studies 35：7，1998，1037～1057

[11]Meyer D.Emergence of the American Manufacturing Belt：An Interpretation.Journal of Historical Geography，IX，1983：145～174

[12]Fujita M.，Krugman P.and Venables A.J.The spatial economy：Cities，regions and international trade.MIT Press，1999

[13]列宁全集（第3卷）.人民出版社，1972：389