分层传递新概率积分三维预测模型：沉陷及溶腔稳定性

第5章　分层传递新概率积分三维预测模型

开采沉陷的有效预测，是减小开采沉陷破坏性的前提条件，直接指导采矿工艺的设计和防护措施的选择。

从研究方法来看，开采沉陷理论可分为两大类［28］，一类是以地表移动作为讨论对象，不考虑岩体特性的唯象学理论研究方法，包括几何理论、非连续介质理论（随机介质理论、碎块体理论、空隙扩散理论）及经验型预计方法（典型曲线法、剖面函数法）等；另一类是以力学原理为基础的正演法和反分析法，通过研究岩体的力学性质及力学行为来研究开采沉陷现象。

唯象学研究方法中，以地表移动作为讨论对象，计算中选用的参数物理意义不明确，很难反映岩层内部的移动规律。因此唯象学研究方法不能很好地解释岩层和地表移动的物理和力学本质。

基于力学的正演法和反分析法，应用力学理论研究岩体力学性质及力学行为，主要包括弹性理论、塑性理论、黏弹塑性理论、断裂理论、损伤力学等。这种方法能对岩层移动过程作出解释，计算中所需参数有各自的物理意义，概念比较清楚。但由于岩体结构及其力学行为、开采实际条件非常复杂，目前还没有成熟的计算岩体力学性态的模型和方法。

因此，综合应用这两种研究手段，在唯象学理论研究方法中，考虑岩体岩性、构造等力学因素是一个很好的解决方法。通过对概率积分法研究和拓展，引入岩石的力学性质，建立适用于岩盐水溶开采沉陷的分层传递新概率积分三维预测模型。

5.1　概率积分方法

5.1.1　基本原理

概率积分法以随机介质理论为基础，用非连续介质模型来模拟岩体［1］。开采引起的岩层和地表移动的规律与作为随机介质的颗粒介质模型所描述的规律在宏观上基本相似。

因此，在图5.1所示的理论模型中，将一个方格的小球移走后，上一层相邻两方格内的小球，将有一个随机滚入该方格，其概率是1/2。若图5.1中a1格内的小球被移走后是a2格内的小球滚入a1格，则a2格将被一个从第3分层的a3或b3格滚来的小球所占据；同样，若是b2格内的小球滚入a1格，则b2格将被一个第3分层的b3或c3格滚来的小球所占据。根据概率相乘和相加定理，a1格的小球的放出，排空a3、b3或c3格这3个事件发生的概率分别为1/2×1/2＝1/4、1/2×1/2＋1/2×1/2＝1/2、1/2×1/2＝1/4；同理，排空第4分层a4、b4或d4格这4个事件发生的概率分别为1/8、3/8、3/8和1/8……如此类推，把各个格子由于各小球的放出而排空的概率写在相应的格子中（见图5.2），就得到颗粒移动概率分布直方图（见图5.3）。

图5.1　随机介质理论模型

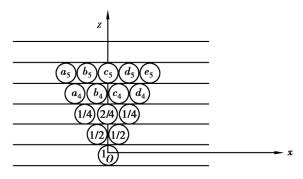
图5.2　随机介质排空概率

图5.3　颗粒移动概率分布直方图

若选取图5.3的坐标xOz，则介质内任意一个z水平的概率分布可以绘成图5.3上方的虚线所示的概率分布直方图。若格子非常小，则这个直方图近于一条光滑的曲线。如果在a1格处放出数量相当多的、其总体积为单位体积的小球，则水平的概率分布曲线趋近于一条正态分布概率密度曲线。

取图5.2中的任意3格相邻的格子A、B、C，它们的中点坐标分别是（x，z＋b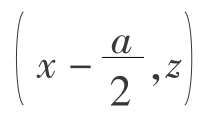），和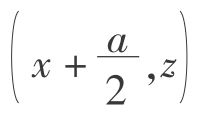，设格子的长和宽分别为b和a，组成图5.4的随机游动模型。

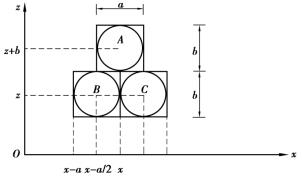
图5.4　随机游动模型

若格子B和C的小球都被移走后，格子B和C中均出现空位，则格子A中的小球在自重作用下可能向B或C空位移动，其概率均为1/2。设P（x，z＋b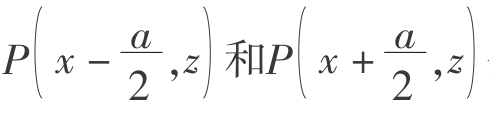）分别表示图5.1中的a1格放出若干个小球时，A、B和C格子中的小球发生移动使相应格子出现空位的概率，则根据概率的相乘和相加定义，可得

若格子非常小，a、b与x、z相比可认为是极小量，则式（5.1）中含有概率P的项可在点（x，z）附近用台劳公式展开得

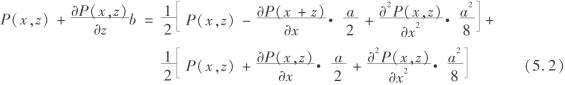
整理后得到

式中 P（x，z）——中点坐标（x，z）的假想格子出现空位的概率。

P（x，z）在岩体内的分布是不连续的。但在格子尺寸非常小，即a→0、b→0时，P（x，z）可近似地看成连续分布函数。因此，现对式（5.3）两边在a→0、b→0的条件下取极限，可得

式（5.4）为图5.1随机介质理论模型岩层移动基本微分方程式，其解P（x，z）为一个连续函数，表示点附近的无穷格子出现空位的概率。令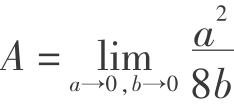，则A为一个反映格子尺寸的常数，则有

对式（5.5）求解，根据该理论模型的假设和采矿实际可得边界条件为

式中 δ（x）——狄拉克函数，其定义为

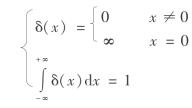
狄拉克函数使下式成立

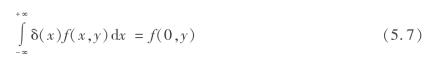
边值条件式的物理意义是只在图5.1所示的理论模型中的格子a1排出数量相当多而总体积为单位体积的小球，其他任何点均不排出小球。这个情况相当于采矿中的单元开采。以此边值条件从基本微分方程解出的P（x，z）表示在单元开采时，点（x，z）附近出现空格的概率。

由边值条件和基本微分方程可得［121］

考虑式（5.7），式（5.8）可化为

令rz＝4Aπz，则式（5.9）可化为

此时，P（x，z）在数值上等于单元开采引起（x，z）点的下沉量We（x，z）。所以，有

式（5.11）即为单元开采时引起点（x，z）的下沉影响函数。相对地面z等于开采深度，为常数。因此，rz也为常数，令其为r（为主要影响半径），则式（5.11）可写为

式（5.12）即为单元下沉盆地的表达式，与正态分布概率密度函数相同。

为了确定单元水平移动作如下假设：在单元开采影响下，岩体产生的变形和移动很小，并且连续分布；在单元开采作用下，岩体虽发生变形，但总体积保持不变。根据弹性力学，材料的体积应变e可表示为3个轴的线应变εx、εx、εz之和：ε＝εx＋εy＋εz。对于图5.1所示的二维情况，有

根据弹性力学公式并考虑本理论模型假设，有

代入式（5.13），可得

对式（5.11）的z求偏导数，可得

对式（5.15）的x积分，可得

将式（5.16）代入式（5.17），可得

将式（5.12）的x求偏导数，代入式（5.18），整理简化后地表单元水平移动表达式为

该方法经国内外多年实践证明具有较高的准确性。已经发展成熟为一种广泛应用于预分析开采沉陷的方法，共有4个主要参数，即下沉系数q，最大影响角正切tanβ，拐点偏距S0和水平移动系数b。

虽然，目前涌现出了许多新的开采沉陷预测技术和方法，但概率积分法仍然是应用最方便和最广泛的方法，近年来，许多学者应用新的技术和理论，对概率积分法进行改进，使其预测精度不断提高。

5.1.2　概率积分法的缺点及改进

概率积分法预计模型作为我国一种较为成熟、也是应用最多的一种开采沉陷预计方法，在实际应用中取得了良好的效果［1］。但是它同时也存在明显的缺陷和不足：

①概率积分法是一种采用唯象学理论，特征研究停留在现象的外观描述上，绕开岩体本身的结构，从地表观测入手，直接将地表沉陷值与地质采矿因素联系起来，在大量的地表观测资料的基础上，进行统计分析，得到描述地表移动变形的统计方法。概率积分法只适用于岩体结构比较简单的情况下，因其简单易行，得到了广泛的应用，但因回避了岩体的本构关系，在岩体结构复杂的情况下，计算误差较大。

②概率积分法是从煤矿巷采的假设推导出来的，适用于固体矿巷采单向推进的二维开采方式，而不适用于岩盐等水溶开采全向推进开采方式的开采沉陷预测。

③概率积分法对非充分采动时预计误差较大。

④概率积分法将整个上覆岩层看成一个整体，作为研究对象，而不考虑各岩层间各种参数，如力学性质、几何尺寸和地质构造的差别，导致预测误差较大。

⑤概率积分将上覆岩层看成各向同性体，由于岩层中裂隙、节理、断层等不连续面的存在，岩层应该表现出各向异性。

针对以上不足，作者将力学研究手段与唯象学研究方法结合起来，推导出适用于岩盐水溶开采的三维模型。研究开采沉陷的分层传递规律，在模型中充分考虑不同岩层岩性的差别，并且在模型建立过程中考虑了裂隙、节理、断层等造成的岩层各向异性等情况。为了区别，将新推导出来的模型称为新概率积分法。

5.2　新概率积分三维预测模型

概率积分法是针对于煤矿巷采情况推导出来的，水溶开采和巷采的推进方式有很大的不同，水溶开采是全向推进，而巷采是单向推进。因此，本书以随机介质理论为基础，应用非连续介质模型来模拟岩体，推导新概率积分三维预测模型，使概率积分方法能够应用于岩盐水溶开采沉陷的预测。

5.2.1　单元开采新概率积分三维模型

理论和实验证明开采引起的岩层和地表移动的规律与作为随机介质的颗粒介质模型所描述的规律在宏观上基本相似［1］。

可构造一个随机介质的三维模型，如图5.5所示。在该三维理论模型中，将一个方格的小球移走后，上一层相邻4个方格内的小球，将有一个随机滚入该方格，其概率是1/4。这样根据概率相乘和相加定理，可以计算出每层中各小球因下一层小球被移走后，而掉入下一层的概率分布，将该概率填入每层小球的方格中，形成每层概率分布图（见图5.6）。

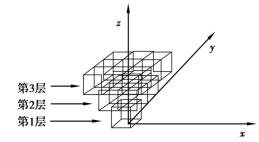
图5.5　随机介质三维理论模型

现在，取任意相邻的5个小球为研究对象，图5.5中的任意5格相邻的格子A、B、C、D、E，设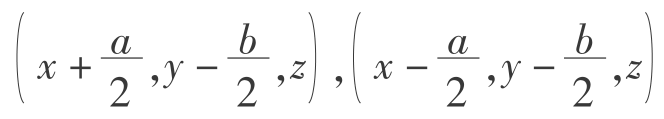格子的长、宽、高分别为a、b、c，则它们的中点坐标分别是（x，y，z＋c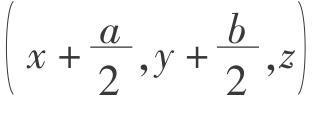），，和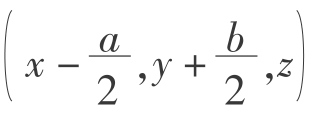，组成图5.7所示的三维随机游动模型。

若格子B、C、D、E中的小球都被移走后，格子B、C、D、E中均出现空位，则格子A中的小球在自重作用下可能向B、C、D、E空位移动，其概率均为1/4。设P（x，y，z＋c），分别表示图

5.5中的最底层放出若干个小球时，图5.7的A、B、C、D、E格子中的小球发生移动使相应格子出现空位的概率，则根据概率的相乘和相加定义，可得

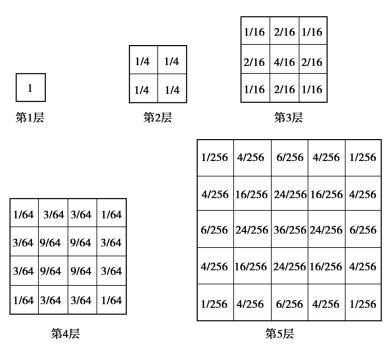
图5.6　三维模型每层概率分布图

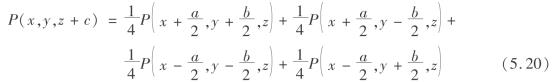
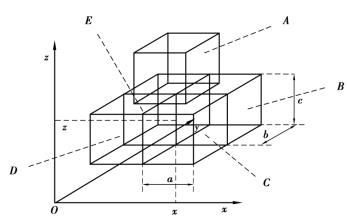
图5.7　三维随机游动模型

假设格子很小，a、b、c与x、y、z相比可认为是极小量，则上式中含有概率P的项可在点（x，y，z）附近用三元泰勒公式展开［123］，取前两项得

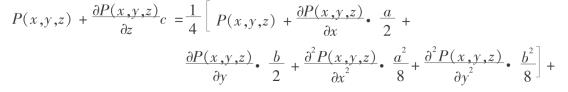
整理得到

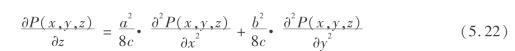
式中，P（x，y，z）表示中点坐标（x，y，z）的假想格子出现空位的概率。P（x，y，z）在岩体内的分布是不连续的。但在格子尺寸非常小，即a→0、b→0、c→0时，P（x，y，z）可近似地看成连续分布函数。因此，现对上式两边在a→0、b→0、c→0的条件下取极限，可得

令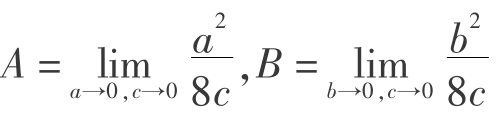，则有

式（5.24）为图5.5三维随机介质理论模型岩层移动基本微分方程式，A、B为反映格子尺寸的常数，其解P（x，y，z）为一个连续函数，表示点附近的无穷格子出现空位的概率。

式（5.24）是一个二阶三维偏微分方程，根据模型假设条件可以得到边值条件为

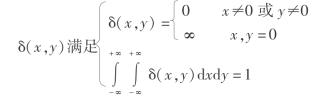
有

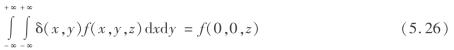
如果将式（5.24）中的z看成时间，则偏微分方程式（5.24），是一个二阶热传导方程［122］，其解为

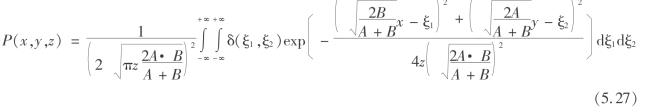
考虑式（5.26），有

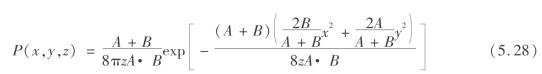
P（x，y，z）在数值上等于单元开采时引起点（x，y，z）的下沉量，用We（x，y，z），则

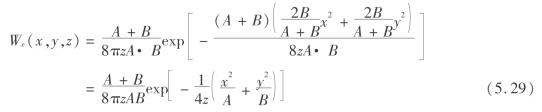
5.2.2　新概率积分三维预测模型

（1）地表沉降预测公式

水溶开采，岩盐以一个中心点向四周溶解，设溶腔空间为V，则水溶开采引起的地表沉陷预测公式推导如下：

因为单元开采地表沉陷公式为

如图5.8所示，整个溶腔开采区域引起的点A（x，y，z）的沉陷量为

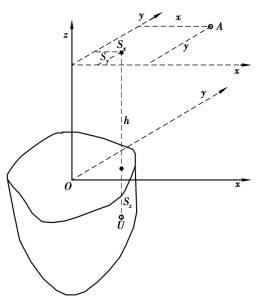
图5.8　水溶开采地表沉陷推导图

考虑到顶板下沉量不可能达到开采高度。因此，整个溶腔开采区域引起的点A（x，y，z）的沉陷量应修正为

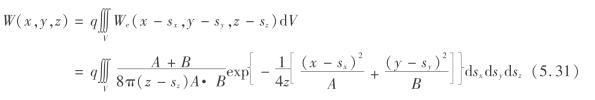
式中　q——地表下沉系数。

对于地表z为常数，等于采深h。因此，上式可写为

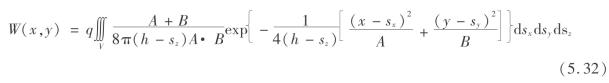
令　rx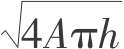＝4Aπh，ry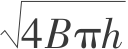＝4Bπh，分别称之为x和y方向的地表影响半径。这样式（5.32）中的A和B可以分别用rx、ry来表示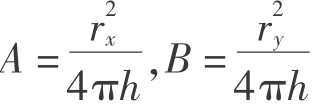：，那么式（5.32）可写为

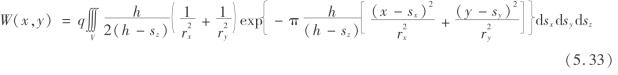
即为开采沉陷新概率积分三维预测模型。

对于煤矿开采，采厚m一般都远小于采深h，而sz＜m。因此，sz≪h。因此，式（5.33）可以简写为

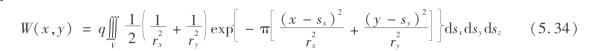
煤矿开采空间规则，大都为长方体，sz与sx、sy无关。因此，式（5.35）可写为

式中　m——煤层厚度；

　S——开采空间上底面方程。

设S在水平面上的投影为D，S的倾角为α，并且沿走向设置为x轴，沿倾向设置y轴，那么，区域S的方程可写为z＝ys tanα，那么

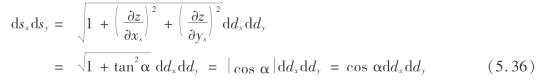
考虑式（5.36），式（5.35）可写为

即为煤矿开采沉陷三维预测模型。

因此，煤矿开采沉陷三维预测模型，是开采沉陷新概率积分三维预测模型的特例。(https://www.daowen.com)

（2）延指定方向的地表倾斜预计公式

地表点A（x，y）延φ方向的倾斜用i（x，y，φ）表示，那么等于W（x，y）在φ方向的方向导数，即

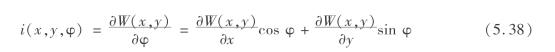
（3）延指定方向的地表曲率预计公式

地表点A（x，y）延φ方向的曲率用K（x，y，φ）表示，那么等于i（x，y，φ）在φ方向的方向导数，即

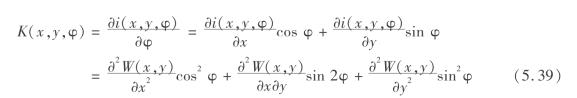
（4）延指定方向地表水平移动预计公式

地表点A（x，y）延φ方向的水平移动用U（x，y，φ）表示，根据水平位移与地表倾斜成正比可得

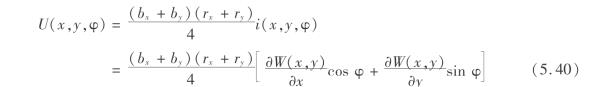
式中　bx、by——x和y方向的水平移动系数。

（5）延指定方向地表水平变形预计公式

地表点A（x，y）延φ方向的水平变形用ξ（x，y，φ）表示，根据水平变形与地表曲率成正比可得

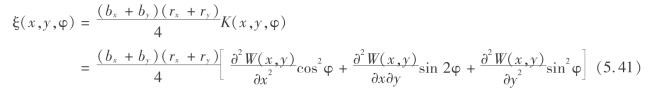
式（5.33）和式（5.38）—式（5.41）是岩盐水溶开采沉陷地表变形预测基本公式，这些公式都是依赖于溶腔形状V的三重积分，如果V很复杂，这些公式一般都不可积，只能通过数值解法进行求解。

在新概率积分三维预测模型的推导过程中，考虑了节理、裂隙、断层等在岩层中可能导致的各向异性情况，引入了rx、ry、bx、by等参数；并针对任意积分区域，解决了岩盐水溶开采形成复杂溶腔的开采沉陷预测问题。

5.3　新概率积分三维预测模型参数及获取

从上面的推导过程可知，新概率积分三维预测模型需要的参数有：开采空间方程V、x方向的主要影响半径rx、y方向的主要影响半径ry、地表下沉系数q、x方向的水平移动系数bx、y方向的水平移动系数by等。其中开采空间方程V由溶腔直接给定，可直接测量获得。主要影响半径、地表下沉系数、水平移动系数的获取比较困难，目前主要通过现场测量数据来获取。

实验和现场数据显示主要影响半径、地表下沉系数和水平移动系数与岩石强度有很大的关系［46-47］。

5.3.1　主要影响半径及力学获取途径

新概率积分三维预测模型，考虑了岩层的各向异性。因此，引入了两个主要影响半径参数：x方向的主要影响半径rx和y方向的主要影响半径ry。主要影响半径是在溶腔边界处，当开采达到充分采动时，地表移动和变形的最大范围（见图5.9）。

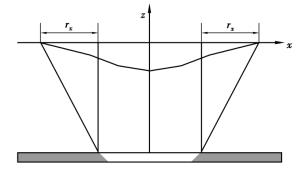
图5.9　x方向的主要影响半径示意图

在三维模型的推导过程中，rx、ry分别表示为

A、B分别为

在随机介质概率积分模型中，将岩石破碎体看成是互不相关的离散单元。a、b、c表示离散单元的尺寸参数。它们分别表示离散单元x方向、y方向和z方向的尺寸。

实验研究结果证明［47］，岩层破坏单元的尺寸能够通过岩层的力学参数来进行计算。

设岩层x方向的抗拉强度为σx，y方向的抗拉强度为σy。

可以用顶板简化为两边固支的梁的理论来计算岩层x、y两个方向的极限破坏强度，由材料力学可知悬臂梁中的应力为

式中　Jz——梁的惯性矩；

y——距离梁中性面的距离；

b——梁的宽度（这里取为单位厚度）；

h——梁的高度。

所以梁中的最大应力为

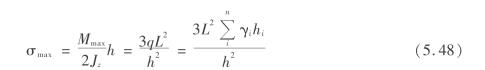
式中　q——梁的均布荷载；

L——梁的长度；

n——岩层数量；

γi——第i层岩层的容重；

hi——第i层岩层的有效厚度。相似材料模拟实验和数值模拟计算均显示梁从固支两端破坏，破坏后的尺寸即为随机介质模型中的介质大小，所以有

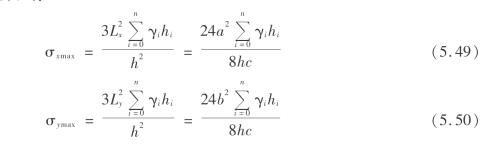
考虑式（5.44）和式（5.45），有

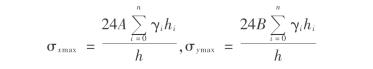
由式（5.42）和式（5.43），可得

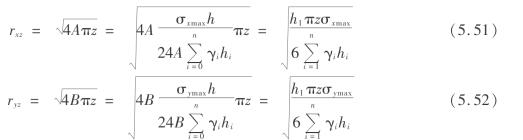
至此，得到了用岩层力学参数表示的rx、ry，在考虑岩层力学参数时，可以充分考虑该方向上节理、裂隙、断层等不连续面对岩层强度造成的影响。从式（5.51）和式（5.52）可以看到，靠近采空区的岩层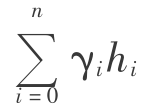很大，因此破坏尺寸较小；随着远离采空区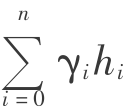，变小，破坏尺寸逐渐变大，这和开采的实际情况相符。

5.3.2　下沉系数、水平移动系数的确定

地表下沉系数是三维预测模型中的关键性参数，其取值的准确性决定了地表移动和变形的精度。目前，大量的实测资料已证实下沉系数与覆岩岩性有关，总体趋势是，岩体越坚硬，其值越小。然而，下沉系数与覆岩岩性之间的定量关系，以及是否与采深和其他因素有关等，还处于探索阶段。焦作矿院邹友峰采用相似第二定律推导出了地表下系数、水平移动系数的表达式，并通过全国大量观测数据，获得了由岩层强度计算的下沉系数和水平移动系数的经验公式［46］。通过推导得出下沉系数和水平移动系数是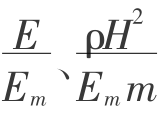的函数。其中，E为岩体综合变形模量，单位MPa；Em为中硬岩体变形模量，单位MPa；ρ为岩体平均质量密度，单位g/cm3；H、m为采深，采厚，单位m。

通过对106个观测站的监测数据进行分析，取Em＝3 600 MPa，ρ＝2.64 g/cm3，可得到下沉系数的经验计算式为

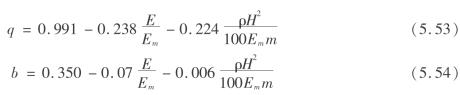
其中，岩体综合变形模量可计算为

式中　n——上覆岩层数。

当然，下沉系数和水平移动系数也可通过现场观测数据获得。

5.4　分层传递新概率积分三维预测模型

在随机介质概率积分模型及推导过程中有这样的假设：随机介质颗粒尺寸一致；整个上覆岩层的下沉系数由一个地表下沉系数来表示。然而，如果将上覆岩层看成一个整体，实际情况与此有较大的差别。很显然，上覆岩层破坏后的颗粒大小并不一致，而与岩层的性质有很大的关系，具有较强的分层特性。

因此，将会出现这样的情况，当移出一个颗粒时，由于颗粒尺寸不一，其上面的颗粒不能马上补充移出的颗粒所产生的空穴，从而控制了其上覆岩层的沉降。只有当开采空间相对于岩土体破碎和断裂后尺寸足够大时，才能充分符合像沙箱模型那样的沉陷过程。上述分析说明，在采空区范围足够大的情况下（充分采动时），上覆岩层的下沉是充分的，概率积分法预计精度是很高的。而在采空区范围较小的情况下，由于某些硬或较硬岩层的作用，阻止了空穴的传递，从而导致概率积分法预计值总是大于实测值的缺陷。

总之，没有考虑岩土体的层状结构、没有考虑不同岩土体的破碎和断裂尺寸是导致概率积分法下沉预计缺陷的根源。因此，有必要考虑不同岩土体的离散尺寸大小，来对概率积分模型进行适当的改进。

可以这样来看开采沉陷，将上覆岩层按岩性分成若干层，对于第1层岩层的移动变形，可以这样考虑：将第2层至地表的岩层移走，用相应的荷载加在第1层岩层上，对于第1层岩层来说其变形和原模型是一致的。这样，在第1层岩层的上表面将产生下沉空间，其形状由第1层岩层的预测参数决定；然后再将第2层岩层还原，在第2层岩层上加上等效的荷载，那么由于第1层岩层的下沉空间，将导致第2层岩层产生相应的下沉空间2。依此类推，直到地表（见图5.10）。这样，可以得到开采沉陷分层传递预测模型为

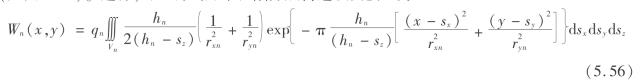
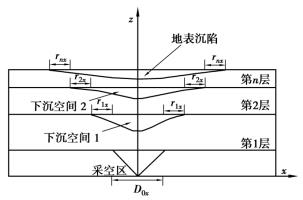
图5.10　分层传递模型

n＝1时，V取溶腔的参数，r、q取第1层岩层的参数。

n＞1时，V取第n-1层岩层下沉空间Wn-1（x，y）的参数，rx、ry、q取第n层岩层的参数。

式（5.56）即为分层传递新概率积分三维计算模型。

用式（5.56）对每层岩层分别进行计算，即可得到地表的下沉预测值。然后再用式（5.38）至（5.41）基于倒数第2层岩层产生的下沉空间，计算地表水平、倾斜等变形值。

在分层传递模型中需要每层岩层的rx、ry和q。rx、ry可以采用5.3.1节的计算方法进行计算；对于q可以采用5.3.2节的经验公式进行计算。

5.5　分层传递新概率积分三维预测模型的数值解法

如果V形状复杂，那么预测模型中的多重积分一般都不可积。因此，必须采用数值解法。对于积分空间V，可以将其离散为若干小的长方体（见图5.11），积分空间可用若干相同的长方体来模拟。设长方体长、宽均为a，高为b。如果a、b足够小，那么一定数量的长方体将趋近于真实的积分域（溶腔），这时可用长方体的型心质点坐标来替代长方体。

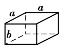
图5.11　积分区域离散

5.5.1　地表下沉数值解算公式

地表下沉公式可离散化为

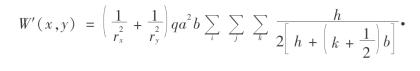
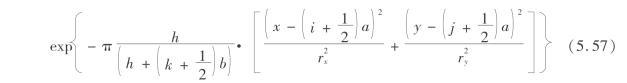
式中 i、j、k——整数，满足于点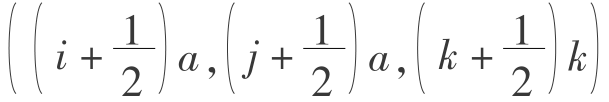在积分空间V内。

5.5.2　延指定方向的地表倾斜数值解算公式

延指定方向φ的地表倾斜公式可离散化为

5.5.3　延指定方向的地表曲率数值解算公式

延指定方向φ的地表曲率公式可离散化为

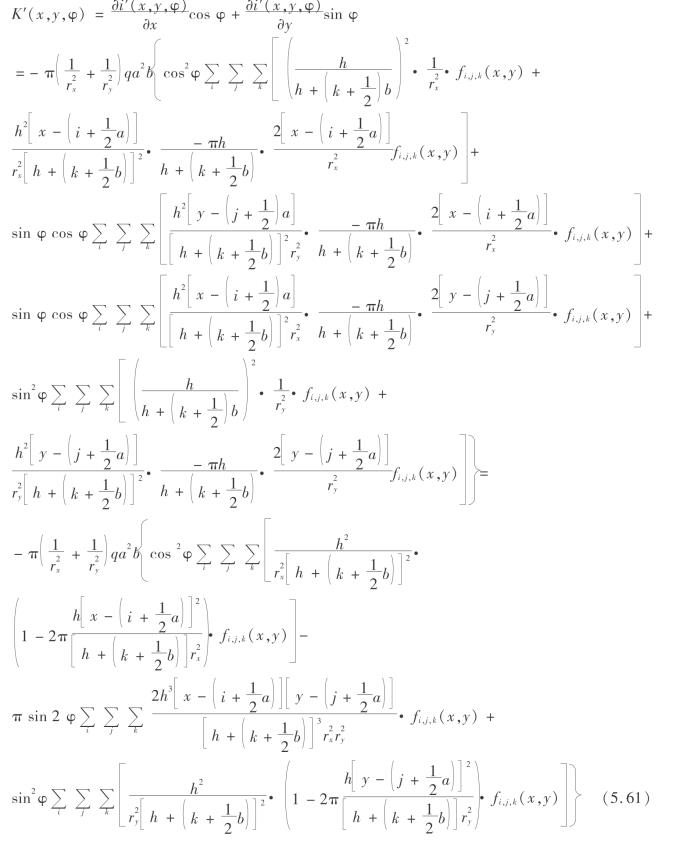
5.5.4　延指定方向的地表水平移动数值解算公式

延指定方向φ的地表水平移动公式可离散化为

5.5.5　延指定方向的地表水平变形数值解算公式

延指定方向φ的地表水平变形公式可离散化为

5.5.6　分层传递模型的数值解法

同样对于分层传递模型的数值化公式为

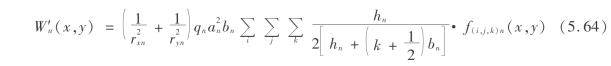
用式（5.64）对每层岩层分别进行计算，即可得到地表的下沉预测值。然后再用式（5.60）至式（5.63）基于倒数第2层下沉空间，计算地表水平、倾斜等变形值。

5.6　多溶腔开采沉陷预测模型

事实上，岩盐水溶开采单溶腔所造成的地表变形是比较小的。但是多个溶腔进行大面积开采时，将会导致严重的沉陷问题。因此，必须对多溶腔情况下的开采沉陷进行预测。

数值模拟证明了在这种情况下可以采用叠加的方法来进行处理，公式为

式中　lix、liy——第i个溶腔中点坐标距原点的距离。

同理可得其他几个公式为

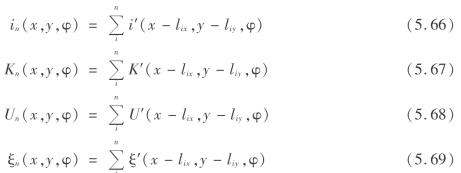
式（5.65）—式（5.69）即为多溶腔开采沉陷预测公式。

5.7　开采沉陷动态预测模型

研究资料表明［1，116-118］，地下开采引起的地表移动变形是一个复杂的四维空间问题。在煤田开采条件下，地表移动过程可从6个月延续到数年，而在盐矿床开采条件下，移动持续时间甚至达到100或100年以上［116］。地表各点处的移动变形值在开采期间变化明显，移动终止时发生压缩变形的区域，在移动期间可能遭受拉伸，反之亦然。因此在进行开采设计和选择地面建筑物保护措施时，不仅要考虑移动过程稳定后的终止状态，还必须考虑地表移动变形随时间的发展过程。

5.7.1　模型原理

假设地表下沉速率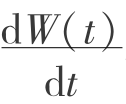与地表某点最终下沉值W0和某一时刻t的动态下沉值W（t）之差成正比［113］为

式中　c——时间影响因素，与上覆岩层的力学性质有关，单位为：/时间。

初始时刻：t＝0，W（t）＝0，对式（5.70）积分，可得

式（5.71）即为地表动态移动过程中的时间函数，令

式（5.72）称为时间影响函数，则

式中，W0如果用开采沉陷分层传递新概率积分三维预测模型进行计算，那么式（5.73）即为开采沉陷分层传递新概率积分三维动态预测模型。

5.7.2　时间影响因素的确定

以往下沉速度系数由地表移动动态的观测资料来确定，可用以下几种方法［120］：

①图解法将实测结果制成下沉时间曲线。该法虽较简单，但受制图精度的限制很不准确。

②对比法将实测结果制成下沉时间过程的无因次曲线，选取适当的系数c，使实测曲线和理论曲线一致，该法求取工作量较大。

③计算法用下沉增量进行计算。

以上3种方法都依赖于实测的动态观测站资料，由于尚未揭示该值的变化规律，对于大多数矿区获取该值都比较困难。

通过对大量观测资料的分析，得到下沉速度系数同以下几个因素有关［119］：

①下沉速度系数与开采速度成正比。如果开采速度是一个变量，则c也应是一个变量。

②下沉速度系数与采深成反比，在其他条件相同的情况下，采深越大，c值越小，反之，也成立。

③下沉速度系数与上覆岩层的性质有关。如果覆岩较硬时，c值较小，覆岩较软时，c值较大。在概率积分法参数中，tanβ也是主要决定于岩层的力学性质的一个参数，如果覆岩较硬时，tanβ值较小，而覆岩较软时，tanβ值较大。因此，c值应与tanβ值成正比。

根据以上分析，可以假定［119］：

式中　v——工作面推进速度，（m/d或m/a）；

　tanβ——主要影响角正切；

　H——矿层开采深度；

　a——待求常数。

　tanβ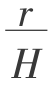＝，在三维模型中，因考虑了岩层在x和y方向的不同，有两个地表影响半径。因此，也有两个主要影响角正切tanβx，tanβy。这里，用两个值的均值来表示tanβ；同样工作面推进速度也用x和y两个方向推进速度的均值来代替v，即

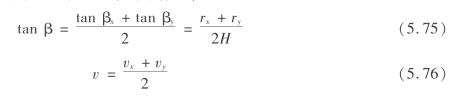
用国内外大量实测数据统计分析后得出，a＝2.0。那么