第4章　水溶开采沉陷有限元数值模拟

近年来，随着有限元等数值计算方法的工程应用，用数值模拟方法来研究开采沉陷成为可能。许多学者在这方面作出了不少有益的尝试。如安徽工业大学的高明中等采用Flac有限差分法对淮南矿区某矿地表沉陷进行了研究［41］；辽宁工程技术大学的唐又持等采用Ansys有限元分析软件对姚桥煤矿西六采区开采沉陷进行了数值分析及预测［42］。

有限元法是求解数理方程的一种数值计算方法，是解决工程实际问题的一种有力的数值计算工具［108-109］。有限元法将求解域看成由许多在节点处互相连接的单元构成，利用单元内假设的近似函数来分片地表示求解域上未知的场函数。这样，一个工程问题的有限元分析中，未知场函数及其导数在各节点上的数值就成为新的未知量，从而使一个连续的无限自由度问题变成离散的有限自由度问题，只要求出这些量，就可以用插值函数计算出各单元内场函数的近似值，从而得到整个求解域上的近似解。显然增加单元的数量或提高插值函数的精度可使近似解收敛于精确解。

开采沉陷过程是在采动情况下上覆岩层的移动、变形和破坏的过程。因此，必须要求有限元程序能够模拟岩层的这一过程。目前的有限元程序还不具备处理破碎岩体的能力。因此，在应用一些有限元软件进行开采沉陷分析时一般采用预先设定破碎带和裂隙带的方法来解决这一难题。破碎带和裂隙带的预先设定一般根据经验公式，会造成较大的误差。

考虑到目前的数值分析软件进行开采沉陷分析的不足，开发用于开采沉陷模拟计算的有限元软件——2D-Sink，在软件中引入了有限元理论的一些最新研究成果。然后采用该软件对岩盐水溶开采沉陷规律进行分析。

4.1　2D-Sink的特点及实现

2D-Sink基于Windows平台，采用VC6.0开发完成，是一种专用于开采沉陷研究的二维有限元分析工具，具备了以下几大特点：

①可视化前处理程序，提供了6节点三角形单元、8节点四边形单元和6节点非线性接触单元，可以方便地建立各种需要的模型，设定复杂的边界条件，自动剖分网格并进行合理的优化。

②可视化后处理程序，可以方便地查看各种等值曲线、云图、矢量图，以及能够方便输出任意节点的各种数据，这对形成开采沉陷的各种变形曲线很重要。

③软件具备多工况处理能力，能够模拟矿物的开采过程。多工况的设置十分方便，施工步数没有限制。

④软件采用增量法，实现了材料非线性处理，能够计算材料塑性变形问题。

⑤2D-Sink采用等带宽储存的LU分解算法，使软件的分析计算速度大为提高。

⑥构建了非线性接触单元，可以模拟层理面、裂隙及断层等不连续面。

⑦采用固定网格法［110，113］，实现渗流等效荷载的计算，使软件能够处理溶腔卤水渗流问题。

⑧采用最新的开挖等效荷载计算公式，避免了传统计算方法带来的误差［110］。

⑨在有限元分析过程中引入了损伤变量和单元破坏判断条件，可以分析岩体的损伤破坏过程。

⑩采用删除破碎单元和弹性加载的方法，实现了开采沉陷中破碎岩体的模拟。

4.1.1　有限元法的开挖

矿物的开采是一个渐进的过程，采空区也是逐步增大的，上覆岩层是伴随着这个过程周处理多工况的能力。

而复始的移动、变形和破坏。因此，用于分析开采沉陷的有限元软件，必须具备在2D-Sink有限元分析软件中，多工况采用分步计算来进行模拟，用前一工况步的计算结果作为后一工况步的初始状态。每一工况步计算模型的环境参数都不相同。因此，每一工况步都必须重新确定边界、计算开挖单元释放荷载、构建新的刚度矩阵、加入新的边界条件，然后解方程，并进行新的迭代分析，解算出工况步的结果（见图4.1）。

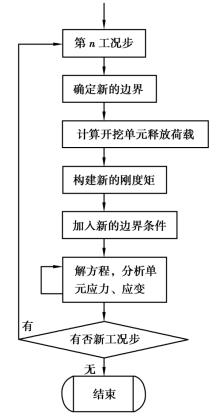
图4.1　多工况处理过程

在多工况处理过程中，开挖单元释放荷载的计算是一个关键问题，目前许多有限元程序未能正确地给出开挖引起的等效节点力［110］。开挖单元释放荷载的计算过程如下：

①遍历整个单元，对开挖单元作下面的处理。

②计算开挖单元等效释放荷载，公式为［110］

式中　ΩE——被开挖掉的那部分单元全体；

　SE——开挖界面；

　B——单元形态矩阵；

　σ——开挖单元产生的内力；

　b——体积力（重力或渗流力）；

　N——型函数。

但目前大多数有限元程序给出的开挖载荷仅含上式右边的第一项，这是最初由Brown等给出的结果［114］，实际上这是不正确的，例如当b是密度时，传统的计算方法就未计入重力对开挖力的贡献。由于开挖往往引起卸荷破坏，因此传统的计算方法可能会低估破坏区，且开挖体的埋深越浅，所引起的偏差就越大［110］。

③遍历结点，对具有开挖释放等效荷载的结点进行荷载集成。

4.1.2　非线性接触元

相似材料模拟实验表明，开采沉陷中层理效应十分明显。同时岩体中不可避免地存在裂隙、节理、断层等不连续面。因此，有限元模拟中必须要能够处理两个物体之间的接触问题。

在实际工程实践中，两个物理单元之间的接触，有两种情况：一种是两个单元固接在一起；另一种情况是两个单元之间在一定的力学条件下将产生滑动或分离。对于第一种情况，按一般的有限元方法进行处理即可。对于第二种情况，介质变成了非连续体，有限元处理起来就有一定的困难，因为在有限元分析中，是不允许单元之间产生滑动和分离的。因此，必须设置一种特殊的单元，使它能在其内部产生滑动和较大的变形来模拟两个单元之间的滑动和分离情况，这种单元称之为非线性接触元。

在2D-Sink中采用的非线性接触元为图4.2所示的六节点单元。1、2、3节点所在的边与4、5、6节点所在的边分别与其他单元连接（见图4.3），这两边之间的距离比起它们本身的长度来说，要小很多，可以忽略。因此与之相连接的单元就相当于相互接触。接触单元内部可以产生较大的变形，用来模拟A、B两个单元之间的分离；接触单元两条长边之间的剪切变形可以用来模拟A、B两个单元之间的滑动。接触单元的实现过程如下：

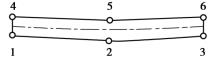
图4.2　非线性接触单元

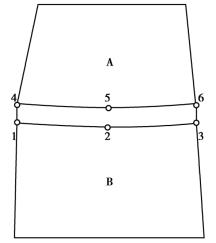
图4.3　非线性接触单元的应用

（1）位移函数和型函数

因为，接触元的宽度比长度小得多。因此，可以将接触元两接触面的位移用中心线（见图4.2中的虚线）的位移来代替。这样就可按一维形式可以构造出接触元的位移函数：

式中　N1、N2、N3——单元型函数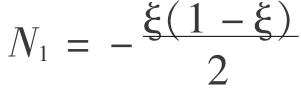，，N2＝1-ξ2，N3＝ξ（1＋ξ）/2。

满足

式中 ξ——接触单元局部坐标。

（2）形态矩阵

令

则形态矩阵可以表示为

式中　h——单元厚度；

　e——接触单元宽度；

按过程进行计算为

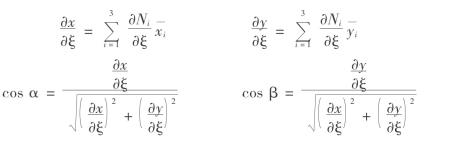
式中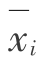——接触元中线3个节点的x坐标，

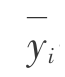　——接触元中线3个节点的y坐标，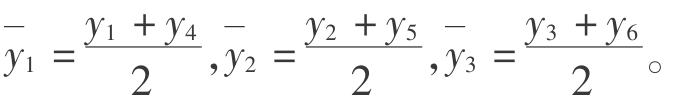

（3）几何方程

几何方程可以表示为

式中　δ——接触单元位移量；

　νs——接触单元剪切应变；

　εn——接触单元法向应变。

（4）物理方程

物理方程可以表示为

式中　τs——接触单元剪切应力；

　σn——接触单元法向应力；

　G——接触单元剪切模量；

　E——接触单元杨氏弹性模量。

（5）屈服条件及非线性分析

令Rt为接触元法向抗拉强度。

①如果σn＞Rt

接触单元将被拉开，这时接触元的两个接触面分开，因此它们之间将不会产生任何力的作用。

②如果σn≤Rt，则要考虑接触单元是否发生剪切破坏。

由库仑摩尔理论，接触单元的抗剪强度为C- fσn；

如果τs≤C- fσn，那么单元将不会发生剪切破坏，这时单元许用应力保持不变；

如果τs＞C- fσn，那么单元将发生剪切破坏，这时单元的法向应力将保持不变，而切向剪应力则应该为sign（τs）fσn。

式中，C为接触单元内聚力；f为接触元摩擦系数，f＝tanφ（φ是内摩擦角）；sign（τs）取τs的正负号。

4.1.3　单元破坏判断条件及处理

单元破坏过程用损伤变量来描述，损伤量可表示为

则

式中　E——无损伤岩体的杨氏弹性模量；

　D——损伤变量，满足0≤D≤1，当值为0时表示岩体完整，当值为1时表示岩体断裂破坏，当值在0～1之间时岩体处于损伤状态；

　E*——损伤岩体的杨氏弹性模量。

单元的破坏过程可以分为拉破坏和压剪切破坏来描述。

（1）单向受拉破坏本构关系及条件

单向受拉破坏本构关系如图4.4所示。其损伤变量可以描述为

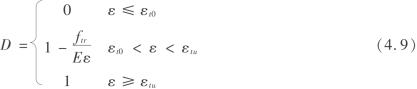
式中　εt0——拉破坏损伤阀值；

　ft——岩体单轴抗拉强度；

　ftr——单元残余强度；

　εtu——极限拉破坏应变，当应变大于该值时，岩体破坏。

由式（4.9）可知，单元拉破坏的初始损伤条件为ε＝εt0，破坏极限条件为ε＝εtu。

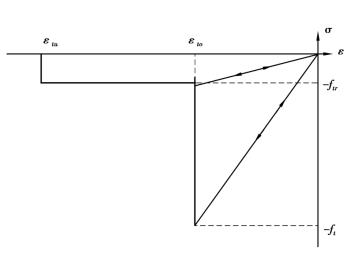
图4.4　单轴受拉时的弹性损伤本构

（2）压剪切破坏本构关系及条件

由库仑摩尔准则定义单元压剪破坏条件为

式中　φ——岩体内摩擦角；

　σ1、σ3——单元最大和最小主应力；

　fc——岩体抗压强度。

在单向压剪条件下，破坏本构关系如图4.5所示，可以描述为

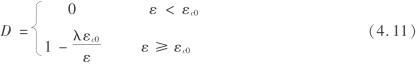
式中　λ——岩体单元残余强度系数，由式λ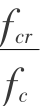＝确定；

　εc0——压剪破坏损伤阀值；

　fcr——单元残余强度。

由式（4.11）可以看出在压剪时单元，损伤初始条件为ε＝εc0，但没有破坏极限条件。因此，可根据实际情况设定单元岩体压剪破坏极限条件。软件中设置极限条件为εc0的整数倍，倍数可自行设置。

（3）破坏单元处理过程

已知有限元数值方法是建立在连续介质力学模型上的。当岩体受力完全破坏后（D＝1），就不再连续，这时有限元方法将不再适用。因此，破坏单元的合理处理是地表沉陷数值模拟的难点。2D-Sink中单元破坏后，表明单元不能再承受力的作用，则删除该单元，并对删除单元按开挖单元进行处理，计算边界开挖等效荷载，反作用于岩体，然后重新建立刚度矩阵和边界条件。破坏单元处理过程如图4.6中虚框内的部分。

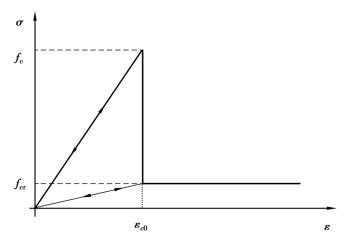
图4.5　单轴受压时的弹性损伤本构关系

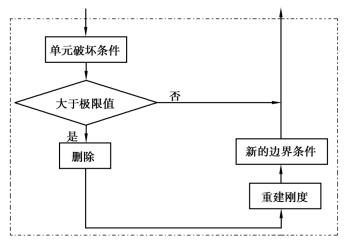
图4.6　破坏单元处理过程

4.1.4　垮塌破碎岩体充填效果模拟

矿物开采后，上覆岩层的受力平衡遭到破坏，岩层必然产生移动、变形和破坏。破碎岩体将充填采空区，破碎岩体的体积始终大于原体积。因此，当破碎岩体充填满采空区和垮塌区后，就能对更上面的岩层产生支撑作用，限制上覆岩层的进一步下沉。也就是说，对于给定的开采高度，即使在充分采动条件下，上覆岩层的下沉值也是有限的，用W0表示充分开采地表最大下沉值为

式中　m——采厚；

　q——下沉系数，由上覆岩层的岩性决定；

　α——岩层倾角。

然而，在有限元中垮塌岩体难以模拟，上覆岩层会失去垮塌破碎岩体的支撑而导致无限下沉，使整个模型的模拟计算不收敛。因此，必须采用一定的办法来模拟垮塌岩体的支撑力。目前的做法是在建立模型时，就确定好破碎带，显然，这一方法有很多不足之处。主要表现在，在模拟计算之前，凭借经验确定的破碎带会有很大的误差。

因此，在整个模拟计算过程中不断地记录垮塌单元体积，当满足式（4.13）时，认为垮塌破碎岩体充填满采空区，可以向上覆岩层提供支撑，所以有

式中　Vp——垮塌单元体积；

　k——垮塌岩体不受压时的碎胀系数，大于1；

　Vk——采空区体积。

垮塌破碎岩体的支撑力采用在采空区边界上加弹性约束的方法来实现。采空区冒落的矸石是一种松散介质。宏观上，它对顶板支撑的力学作用可以近似地用弹性支撑体表述。需要考虑的是，随着工作面的推进，矸石在覆岩作用下逐步被压实，材料的密度ρ、弹性模量E和泊松比μ随时间而增加。反映上述参数的变化规律［116］的经验公式为

式中　ρ——材料的密度，kg/m2；

　E——弹性模量，MPa；

　μ——泊松比；

　t——时间，单位年。

4.1.5　渗透作用下的等效节点力的计算

岩盐水溶开采，卤水的渗透性对顶板有很大的影响。因此，用数值方法模拟水溶开采沉陷，必须要考虑水的渗透作用。

本文采用固定网格法来处理渗流问题［110］。既然是在固定网格上求解有自由面的渗流问题，那么所求得的自由面势必切割一部分单元，但如何求得这部分单元在渗流作用下的等效节点力，采用如下的方法：

在渗流场中的任一微元体所受到的单位体积的渗透力［115］为

式中　γw——水的密度；

　φ——水头值。

在被浸湿的单元e内的任意点为

式中　ne——单元e的节点数；

　φ（i，e）——单元e第i个节点的水头值。

将式（4.16）代入式（4.15），然后利用式（4.17）求得单元i在渗透作用下的等效节点力为

式中　Ng——单元e的高斯点数目；

　W（ig）——对应高斯点ig的权系数；

　J（ig）——是相应的雅可比（Jacobian）值；

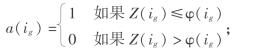
　Z（ig）——对应高斯点的垂直坐标。即对于被自由面所切割的那些单元而言，若其高斯点位于自由面以上，则其对等效节点力将没贡献。

4.1.6　材料非线性问题处理方法

材料非线性是指当岩体载荷达到一定值时，岩体的物理方程不再保持线性状态。岩体的应力应变关系发生变化，岩体进入塑性区或岩体发生蠕变等，前者是不依赖于时间的弹塑性问题，而后者则是与时间有关的黏（弹、塑）性问题。本软件只考虑了岩体的塑性问题。

（1）塑性强度理论

目前有很多种塑性强度理论及屈服函数，各种不同的强度理论仅能较好地反应部分材料的破坏形式，而没有一种对所有材料都适用的强度理论。因此，为了在有限元分析时能够根据不同的材料选择适当的强度理论，在2D-Sink中，设定有两个单剪理论：特雷斯卡（Tresca）准则、摩尔库仑准则（Mohur-coulomb）；两个三减强度理论：广义米赛斯准则（Mises）、Prager-Drucker准则，共4种强度准则。

1）单剪应力理论——特雷斯卡（Tresca）准则

Tresca准则是一种单剪强度理论，只考虑最大剪应力的影响，只要最大剪应力超过了材料的抗剪强度，则认为材料进入塑性状态。其屈服函数可表示为

式中　σ1——第1主应力；

　σ3——第3主应力；

　s——抗剪强度。

2）单剪切角理论——摩尔库仑准则（Mohur-coulomb）

摩尔库仑准则也是一种单剪强度理论，它不考虑主应力，只考虑最大主剪应力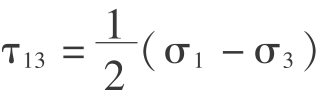，但并不是直接用最大剪应力超过材料抗剪强度来判断材料是否屈服，采用的屈服函数为

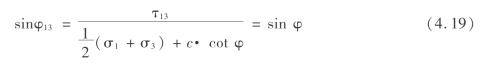
式中　c——材料内聚力；

　φ——材料内摩擦角。

3）三剪应力理论——广义米赛斯准则（Mises）

该理论综合考虑了3个剪切应力的作用，屈服函数可以表示为

式中 τ12、τ23、τ13——材料3个面的剪切应力。

4）广义三剪应力理论——Prager-Drucker准则

该理论考虑了3个主应力的影响，屈服函数可以表示为

式中 σ1、σ2、σ3——材料的3个主应力。

5）强度准则的统一表达形式

在π平面上可以将不同的强度准则用统一的函数形式表达为

式中　I1——应力张量第1不变量；

　J2——应力张量第2不变量；

　J3——应力张量第3不变量；

　θ——骆得角（lode）。

这样Tresca准则可表示为

(www.daowen.com)

库仑摩尔准则可表示为

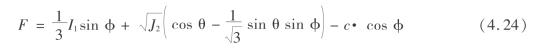
广义米赛斯准则可表示为

Prager-Drucker准则可表示为

式中 a、k——与材料内摩擦角φ和黏聚力c有关的常数。

F＜0时，材料处于弹性状态；F≥0时，材料就进入塑性状态。

（2）流动法则

流动法则规定塑性应变增量的分量和应力分量以及应力增量分量之间的关系可表示为

式中　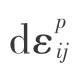——塑性应变增量的分量；

　dλ——待定有限量，与硬化法则有关；

　F——塑性势函数，后续屈服函数。

（3）硬化法则

硬化法则规定材料进入塑性变形后的后续屈服函数。一般采用的形式为

式中　k——硬化参数，依赖于变形历史；

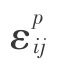　——塑性应变。

对与理想弹塑性材料，因无硬化效应，则后续屈服函数和初始屈服函数一样。

硬化法则有各向同性法则、运动硬化法则以及混合硬化法则，本文采用了能适应材料一般特性的混合硬化法则，即既考虑了各向同性法则，又考虑了运动硬化法则。这样，可将应变增量分为共线的两部分，即令

式中　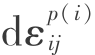——与屈服面扩张相关联的部分塑性应变增量；

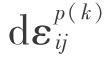　——与屈服面移动相关联的部分塑性应变增量。

并且满足

式中　M——混合硬化参数，表示各向同性硬化特性在整体硬化特性中所占的比例。

后续屈服函数可表示为

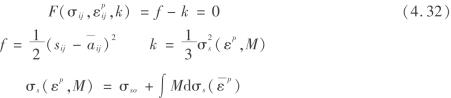
（4）加载、卸载准则

加载、卸载准则是判断进入塑性状态的材料是继续保持塑性加载还是弹性卸载。这一判断将决定在后续分析中是采用弹性本构关系还是继续采用塑性本构关系。

加载卸载准则可以表示为

①若F＝0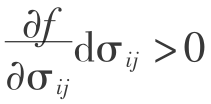，，材料继续塑性加载。

②若F＝0，，材料由塑性向弹性卸载。

③若F＝0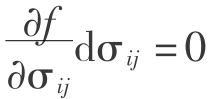，，对于理想弹塑性材料，为塑性加载；对于硬化材料，此时为中性变载，仍保持塑性状态，但不产生新的流动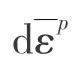（＝0）。

以上各式中，F为后续屈服函数。

（5）塑性矩阵

由屈服函数、流动法则以及硬化法则可以导出材料塑性矩阵［121］为

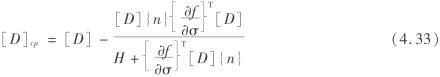
式中　［D］——弹性矩阵；

　｛n｝——流动矢量；

　H——硬化模量。

（6）有限元增量形式

有了塑性矩阵，就可以写出塑性增量方程为

用虚位移原理可以得到有限元系统平衡方程为

式中　τKep——弹塑性刚度矩阵；

　Δa——增量位移向量；

　ΔQ——不平衡力向量。

以上3个量都由各单元相应量集成而成为

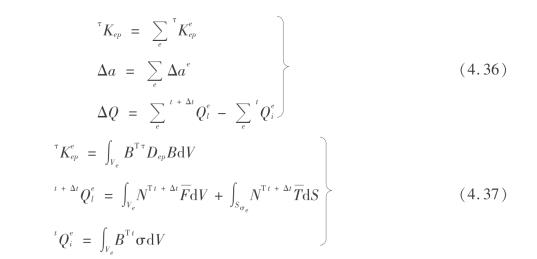
由式（4.35）解得Δa，由几何关系得到Δε＝BΔae，然后由式（4.34）得到Δσ，于是可得到t＋Δtσ＝tσ＋Δσ。然后再将t＋Δtσ代入式（4.35），直到ΔQ满足收敛条件为止。

4.1.7　非线性方程组的解法

对于弹塑性问题式（4.35）是一个非线性方程组，其中τKep依赖于未知量Δa，因此不能直接求解。软件采用Newton-Raphson方法对非线性方程组进行求解。

那么式（4.35）可写为

式中　n——迭代次数，n＝1，2，3，…

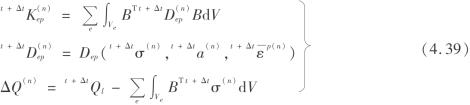
第一步有

具体迭代步骤：

①由式（4.39）计算t＋Δt K（ep n）和ΔQ（n），构成方程式（4.38）。

②按线性方程组的解法（4.2.8节）求解方程式（4.38），得到本次迭代的位移增量Δa（n）。有t＋Δt a（n＋1）＝t＋Δt a（n）＋Δa（n）。

③计算各单元的应变增量和应力增量为

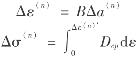
式中　Δε（n）′——Δε（n）的塑性部分。

由此，有

④用收敛条件判断是否收敛，如收敛则结束计算，相反则进入下一迭代步。

一般有位移收敛、平衡收敛和能量收敛3种收敛条件。软件采用了位移收敛条件为

式中 erd‖t a‖——给定的容许误差。

4.1.8　线性方程组的数值解法

有限元分析中，有很大一部分工作是解线性方程组，因此有

式中　K——刚度矩阵；

　a——要求解的位移矩阵；

　P——模型受力条件。

随着模型结点数的增加，刚度矩阵K的大小将以几何速度增长。表4.1是二维有限元分析中节点数与刚度矩阵的维数以及完全存储所用的计算机内存。

表4.1　刚度矩阵的大小、需要的计算机内存与节点数的关系

?

由表4.1可见，随着节点数的增加，计算机内存的消耗是惊人的。因此，必须找到更为有效的矩阵存储和方程解算方法。2D-Sink采用了等带宽来存储刚度矩阵，采用LU分解来解算线性方程组。大大节约了内存和提高了解算速度，表4.2是完全存储LU分解法和半带宽存储LU分解法对相同模型解算时间的对比。

表4.2　直接存储和等带宽存储LU分解算法比较

从表4.2可见，半带宽存储对解算速度有十分显著的提高。

从有限元理论知道，刚度矩阵K是对称矩阵，并且其数值全部集中在宽度为D的条带之内，在条带之外的数值全为零。因此，可以通过只存储条带内的数据，来减少刚度矩阵的存储量（见图4.7）。可以将刚度总大小由（2n）2减小到2n×D，在通常情况下D远小于2n。

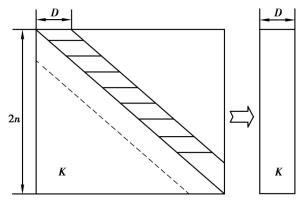
图4.7　半带宽存储

D可确定为

式中　Di——结点i的最大相关结点差值。

由式（4.42）可见，如果合理调整结点编码，可以有效减小内存的需求量。

两个矩阵元素的对应关系可确定为

式中　i*——等带宽矩阵中的行标；

　j*——等带宽矩阵中的列标；

　i——全阵中的行标；

　j——全阵中的列标。

因此，进行解算时，只需要在等带宽矩阵中按式（4.43）找到全阵中的对应元素即可，代入LU分解算法即可求解。

4.2　水溶开采沉陷有限元数值模拟

参照某盐矿的实际情况地层情况，对水溶开采沉陷进行有限元数值模拟，以期获得水溶开采沉陷的一般规律，为水溶开采沉陷预测模型的建立打下基础。

4.2.1　地层条件及力学参数

在进行模型构建时，将上覆岩层中岩性基本一致的岩层进行了复合处理。复合处理后形成7个复合岩层，其力学参数见表4.3。

表4.3　计算模型所用的岩石物理和力学参数

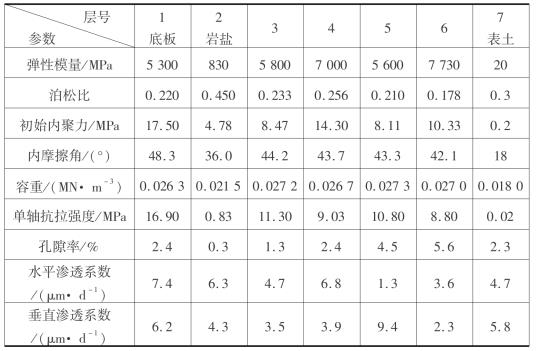
各复合岩层的物理力学参数根据复合岩层中各组分岩层的物理力学参数按其厚度进行加权平均处理计算获得，即

式中　xi——相应复合岩层中第i分层的某物理力学参数在该复合岩层的加权平均值；

　hi——相应复合岩层中第i分层的厚度，n是相应复合岩层中所包含的地质自然分层数。

4.2.2　模型建立

本文共建立了6种模型进行数值模拟研究。为研究层理对开采沉陷的影响，建立了一种不考虑层理的单溶腔模型；为了研究不同倾角岩层的开采沉陷规律，分别建立了水平、15°、30°3种倾角岩层单溶腔模型；为了研究断层对开采沉陷的影响，建立了一种含有断层的模型；为了研究大范围多溶腔开采沉陷规律，建立了一种多溶腔模型。在这些模型中，后5种都考虑了层理面。

（1）模型尺寸及网格划分

模拟开采沉陷规律必须模拟整个上覆岩层。因此单溶腔模型的宽度为2000 m，高度为690m；多溶腔模型的宽度为2800m，高度为690m。

网格（grid）的布置从岩盐开采处向四周逐渐变梳。单溶腔模型溶腔布置在模型盐层中心，最大跨距180m；多溶腔模型共在岩盐层等间距分布4个溶腔，溶腔间距110m，溶腔跨距180m。模型网络划分如图4.8至图4.12所示。

图4.8　水平岩层单溶腔网格模型

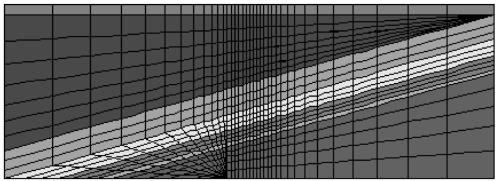
图4.9　15度倾角岩层单溶腔网格模型

图4.10　30度倾角岩层单溶腔网格模型

图4.11　断层单溶腔网格模型

图4.12　多溶腔网格模型

（2）边界条件

由于计算模型模拟全高，模型上边界是地表为自由边界；模型左右两边离岩盐开采处很远，开采对其水平位移的影响可以不计，因此，对这两边加上水平方向固定约束；开采对模型下边界的垂直位移影响可以不计，因此，下边界加上垂直方向固定约束。水溶开采过程中，溶腔内有水压，会对溶腔顶板提供一定的支护作用，因此，每一步开挖后在溶腔壁上加上水压。模型边界条件如图4.13所示。

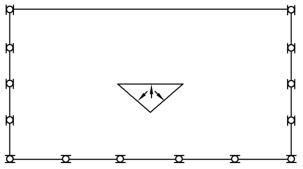
图4.13　模型上施加的载荷

（3）开挖过程

根据相同地质条件溶腔顶板完全破坏，溶腔报废时，溶腔的最大顶板跨距。每个溶腔分别设置3步开挖，每步开挖60 m，共开挖180 m。图4.14所示是模型分3步开挖后形成的溶腔。

图4.14　岩盐分步开挖形成溶腔

4.2.3　模拟结果及分析

（1）开采沉陷层理效应分析

层理是上覆岩层中的软弱薄层，是两个岩层之间的交接面，其力学性质较岩层本身要差很多。在进行有限元分析时，如果不考虑层理，那么，两个相邻岩层将固接在一起，必须满足连续变形；而实际情况是，当矿物被不断开采出来后，采空区逐渐扩大，将会在上覆岩层的某些层理间产生滑动或分离（离层），使相邻的两岩层不满足连续变形条件，这样不可避免地造成计算误差。其中离层的现象在相似材料模拟实验和数值分析中都可直观看到（见图3.16、图4.15）。因此，在进行有限元数值模拟时必须考虑层理。本文模型中的层理用非线性接触元进行模拟。

图4.15　开采过程中离层的产生

数值模拟结果表明层理对开采沉陷影响十分显著，用有限元模拟开采沉陷时，是否考虑层理，对预测精度有很大影响。在同样的地层和开采条件下，考虑层理模拟计算的地表最大下沉值和最大水平位移分别为0.181m和0.073m，而不考虑层理的计算结果分别为0.158m 和0.055 m。表4.4和表4.5列出了两种情况下3个开挖步的最大垂直和水平位移。可以看到，随着开采宽度的增加，层理的影响会越严重，不考虑层理将会导致模拟出现较大误差。

表4.4　考虑层理和不考虑层理时的最大下沉值

表4.5　考虑层理和不考虑层理时的最大水平位移值

开采沉陷的层理效应可以如下解释：

上覆岩层中的层理改变了其整体刚度，如果没有层理，上覆岩层相当于几个岩层黏合在一起组成一个厚度较大的梁或板，由于其厚度大，所以刚度很大，刚度大的厚硬岩层在岩层移动的发展过程中起着至关重要的作用，它的弯曲、稳定或断裂在很大程度上决定了地表下沉值的大小。因此，在弹性模量取值合理的条件下，用不设置层理的有限元计算模型得到的地表下沉值总是远小于工程实测值。设置层理以后，相当于原来刚度大的岩梁被层理面分隔成几个刚度较小的岩梁，刚度小了，在相同的开采程度下，就会产生更大的挠度或更易于失稳破坏，地表下沉值也相应增大。

（2）水平岩层开采沉陷规律

第1步开挖后，顶板悬空，在层理处的应力分布有压应力和切向应力，由于层理力学性质较岩层要差许多，切向应力将会导致层理产生相对滑动，从而破坏掉层理的完整性，使层理不能承受拉应力。但这时，由于悬空范围不大，两岩层间的垂直位移一样，水平位移不同，虽然层理破坏但还不会出现离层；第2步开挖后，顶板悬空距离增大，层理处仍然分布有压应力和切向应力，在切向应力的作用下，层理滑动范围增大，仍没有产生离层；随着第3步开挖的进行，顶板悬空距离继续增大，使层理上下面分离产生明显离层，离层最大分离距离为0.141 m（见图4.15）。悬空使顶板承受较大拉应力，拉应力使顶板破坏，破坏高度45 m（见图4.16）。

图4.16　顶板破坏范围

图4.17是水平单溶腔模型3步开挖形成的地表下沉曲线和地表水平位移曲线图。3步开挖导致地表的最大下沉值分别为0.032 m、0.097 m、0.181 m，地表最大下沉点在岩盐开始溶解点的正上方，曲线以最大值处为中点，左右对称分布；最大水平位移值分别为±0.013 m、±0.039 m、±0.073 m，对称分布于岩盐开始溶解点正上方的两旁，最大值的位置偏向于溶腔方向。

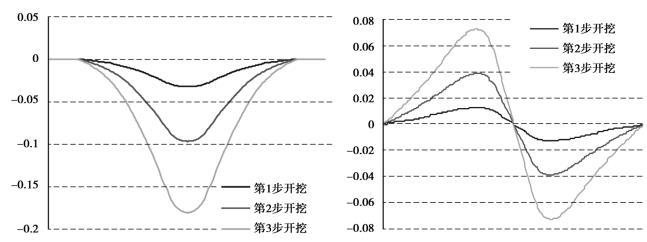
图4.17　水平岩层地表下沉和水平位移曲线

（3）开采沉陷倾斜效应分析

图4.18和图4.19分别是15度和30度倾角岩层开采地表下沉曲线和水平位移曲线图。

可以明显看到，地表最大下沉值位置向下山方向偏移，15度模型3步开挖的偏移量分别为8.06 m、16.13 m、24.19 m，30度模型3步开挖的偏移量为83.3 m、89.74 m、96.15 m。可见顶板跨距的增大或岩层倾角的增大，都将导致偏移量的增加；水平位移在下山方向的最大值比上山方向大，15度模型3步开挖分别相差0.002 m、0.004 m、0.018 m，30度模型3步开挖分别相差0.015 m、0.022 m、0.028 m。可见顶板跨距增大或倾角增大，都将导致差值的增加。15度模型的最大下沉值为0.175 m，最大水平位移值为0.080 m；30度模型的最大下沉值为0.140 m，最大水平位移值为0.108 m，可见随着倾角的增加，在开采相同量的岩盐时，地表最大下沉值将减小，而地表最大水平位移值将增加。

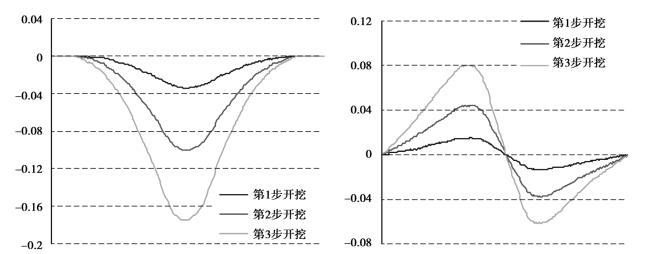
图4.18　15度倾角地表下沉和水平位移曲线

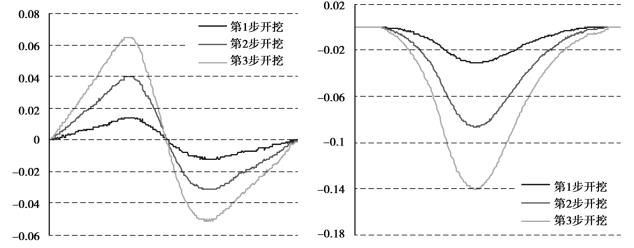
图4.19　30度倾角地表下沉和水平位移曲线

（4）开采沉陷断层效应分析

图4.20是含有断层的模型开采地表下沉曲线和水平位移曲线图。

可以看到，断层对开采沉陷的影响十分显著。3步开挖的地表最大下沉值为0.033 m、0.099 m、0.194 m；地表最大水平位移值在无断层方向为0.013 m、0.035 m、0.067 m，有断层的方向为-0.007 m、-0.03 m、- 0.062 m，两边有一定差值，有断层方向的水平位移较小。与无断层水平模型相比，断层引起地表下沉值增大，水平位移值减小。同时断层的存在使地表最大下沉点向无断层方向偏移，水平位移的零点向无断层方向偏移，也就是说在有断层的一边，开采影响范围要大一些。随顶板跨距的增加，水平位移的零点也向无断层方向偏移。

地表下沉和水平位移曲线

（5）多溶腔开采沉陷规律

图4.21是4个溶腔开采时，形成的地表下沉曲线和水平位移曲线，可见其形状与单溶腔开采时相似，只是数值大得多。相同地质条件下，多溶腔模型3步开挖的最大下沉值分别为0.079 m、0.254 m、0.56 m，比单溶腔分别大2.5、2.6、3.1倍；3步开挖的地表最大水平位移值分别为±0.029 m、±0.094 m、±0.205 m，比单溶腔分别大2.2、2.4、2.8倍。

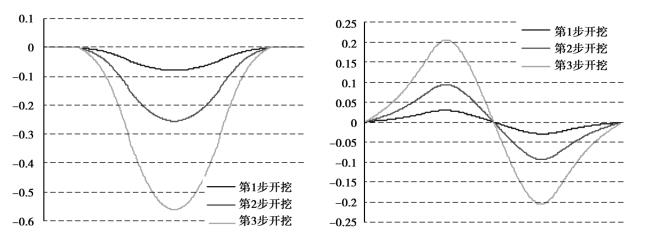
图4.21　多溶腔地表下沉和水平位移曲线

数值模拟结果显示，多溶腔开采时，在距顶板一定距离的岩层内会出现波浪形曲线。图4.24是距顶板115 m处岩层的下沉曲线和水平位移曲线，两个图形呈现明显波动现象。但是这种现象会随着距顶板距离的增大而逐渐消失，变成和单溶腔开采相似的曲线。图4.23是溶腔顶板上221 m处的下沉曲线和水平位移曲线。这时，下沉曲线的波动基本消失，而水平位移曲线还有一定波动。直到顶板上225 m处（见图4.22），多溶腔开采造成的波动才基本消失，岩层移动和变形曲线的形状与单溶腔开采相似。因此，多溶腔开采引起的波动效果的影响范围，大约为采厚15倍，并且水平位移的波动范围比垂直位移范围大。

（6）开采沉陷叠加原理

将地层条件完全相同的单溶腔模型，作完全相同的开挖模拟计算，得到地表下沉曲线和水平曲线后，按以下方式进行叠加：

设单溶腔开采地表下沉曲线方程为Ws（x），那么多溶腔叠加的方程为

式中　n——溶腔数量；

　li——第i个溶腔中点距原点坐标的距离。

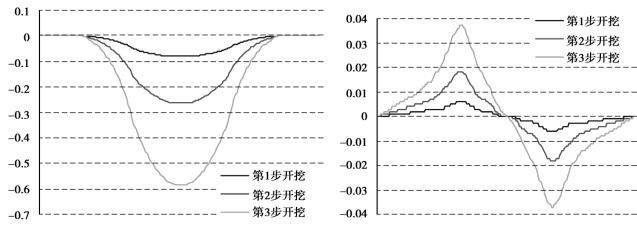
图4.22　多溶腔顶板上255m处下沉和水平位移曲线

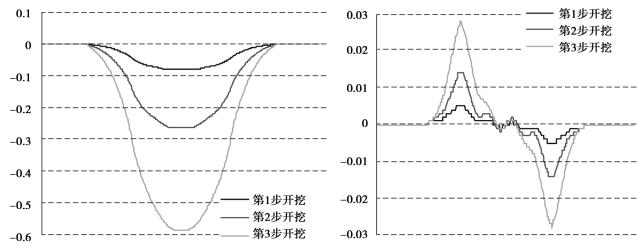
图4.23　多溶腔顶板上221m处下沉和水平位移曲线

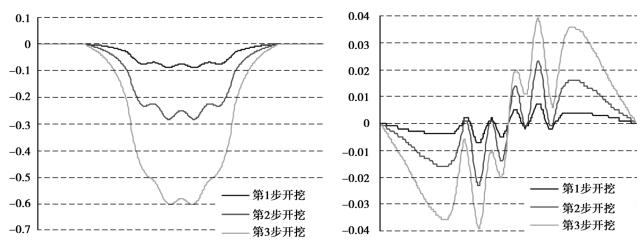
图4.24　多溶腔顶板上115m处下沉和水平位移曲线

如图4.25所示为叠加后的地表下沉曲线和地表水平移动曲线，将它们与4溶腔模型的地表下沉曲线和水平移动曲线（见图4.21）进行比较，可以发现它们的形状几乎一致，最大下沉值完全相同为0.56 m，最大水平位移值也基本相同，相差0.005 m。因此，多溶腔开采的地表变形可以用单溶腔开采的地表变形曲线叠加而得到，这一点对多溶腔开采沉陷预测十分重要。

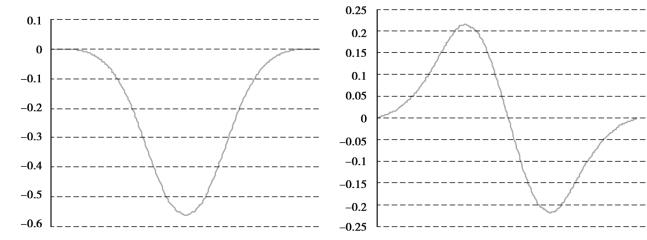
图4.25　4个单溶腔模型叠加后的下沉曲线