第3章　岩盐水溶开采沉陷相似材料模拟实验

相似材料模拟实验自1937年在苏联全苏矿山测量科学研究院首次用于研究岩层与地表移动问题至今，作为室内研究的一种重要手段，具有研究周期短、成本低、成果形象直观等特点，特别是能对影响因素进行重复分析，已被广泛用于矿山开采沉陷规律研究中，与实地观测和理论研究相配合，对指导建筑物下、铁路下、水体下压煤开采实践，发挥了重要作用［87-91］。

该方法根据相似原理在主要满足几何相似和力学相似的基础上，考虑到边界条件和初始条件相似及生产工艺的影响，参照现场实际地质及生产条件，采用与天然矿岩物理力学性质相似的人工材料，按比例做成模型，并在模型中进行采掘实验。观测模型的变形、位移及岩层破坏的发生发展过程，从实验结果按相似原理推测原型中发生的情况。这种方法克服了现场生产中矿山压力显现及上覆岩层移动的“不可见性”，形象直观地反映了矿山生产过程中的力学现象，可在较短的实验周期内，完成整个生产过程的模拟［92］。

3.1　实验目的及方案

3.1.1　实验内容及目的

应用相似材料模拟实验，对岩盐水溶开采沉陷进行研究，主要研究内容有：

①上覆岩层损伤演化过程及规律。

②上覆岩层移动、变形和破坏规律。

③开采沉陷的层面效应及分层特性。

④开采沉陷岩层破碎岩体尺寸特性。

通过对以上内容的研究，再现上覆岩层的移动、变形和破坏过程。获得岩盐水溶开采沉陷上覆岩层及地表变形规律。了解开采沉陷按岩层性质而产生的分层特性及上覆岩层移动变形过程中表现出来的层面效应，这将是地表沉陷的前提条件［93］；得到岩层破碎岩体尺寸与岩层力学性质的关系，以及获得岩层在开采沉陷过程中的损伤演化方程。

3.1.2　实验方案

依据库兹涅佐夫的建议［94］：如果平面应力模型前后垂直暴露面能保持稳定而不破坏，用平面应力模型模拟现场的平面应变情况，就可得到相似的应力和应变分布特征。针对以上研究目的，本文拟采用长1.5 m，宽0.3 m，高1.2 m的转体实验台，作平面应变相似材料模拟实验来进行研究（见图3.1）。该实验台的一端安设有转动轴，模型实验台可在垂直面内转动，可用来模拟缓倾斜盐层。

图3.1　转体模型实验台

模型的载荷主要是自重，为了全面了解上覆岩层的移动、变形和破坏过程，本文模拟全高，模型不用施加外力。

相似材料模拟实验要求模型与原型的岩层厚度，采深以及开采空间的几何尺寸均应满足几何比。一般来说，模型几何比越大，其精度越高，越能反映原型的实际情况，但所需成本和时间也越多。况且，几何比的确定还要受模型的外形尺寸及其稳定性和加载设备等的限制。因此，矿山压力模拟实验一般选取的定性模型几何比为1∶200～1∶100，定量模型几何比为1∶50～1∶10。但是，如果采取适当措施，小几何比模型也能保证实验精度。如在水工和土木工程研究中，葡萄牙国家土木工程研究所就用1∶500～1∶200的小几何比模型进行研究，取得良好效果。清华大学水利系在进行某重力拱坝三维小块体地质模型实验时，就曾采用1∶300的小几何比并取得了良好效果。实践证明，只要材料性能合适，在提高加工精度及砌筑工艺水平，采取可靠的加载措施及较高精度的量测设备等技术措施的基础上，适当缩小模型的几何比是可行的［2］。由于本次实验选取的平面实验台，其高度限制了几何比的选取。故本实验采用较好的模拟技术措施和高精度的测量手段，选取模型几何比为1∶300。

按实验台尺寸，模型模拟高度为

1.2×300＝360 m

模拟长度为

1.5×300＝450 m

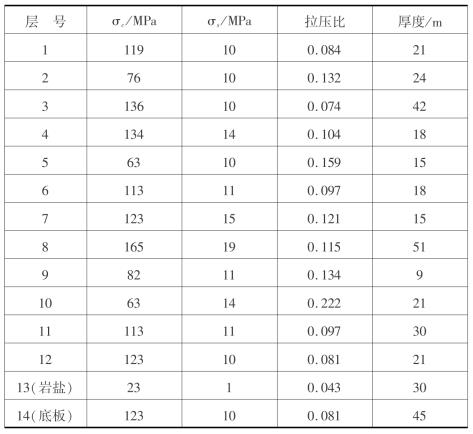
模型共14个自然分层，从上到下依次排序，其中第14层为底板岩层，第13层为矿物层（岩盐），12层上覆岩层，各岩层的性质分布如表3.1所示。

表3.1　各岩层物理力学性质

3.1.3　实验设备及耗材

所需实验设备有相似材料模拟实验台、EMS-2型工程多波地震仪、高解析度数码相机、笔记本电脑、摄像头、小钢尺及各种连线等。

所需耗材有河沙、石膏、石灰、染料、水等。其中，河沙为骨料，石灰、石膏为胶结物，染料用于区分岩层。

3.2　测量系统

本文实验测量的数据有开采过程中模型的力学参数及岩层损伤情况；上覆岩层的位移情况；上覆岩层的移动、变形、破坏过程等。针对这些目的，采用了以下测量方法：

3.2.1　模型力学参数及损伤量测量

本文采用声波测量方法来对开采过程中岩层的力学参数及岩层的损伤演化情况进行测量。使用EMS-2型工程多波地震仪（见图3.2），测定每次开采后岩层的纵波波速和横波波速，然后解算出岩层的力学参数和损伤情况。

图3.2　EMS-2型工程多波地震仪

EMS-2型工程多波地震仪适用于多波分量地面勘探，多波联合勘察，瑞雷波勘探等。可以实现许多测量功能，本文主要采用该仪器来实现相似模型在开采的影响下，力学参数的变化过程及岩层损伤量演化过程。

（1）仪器可行性

本文要测量的是模拟模型，相比实体在几何尺寸上要小很多。因此，对仪器的采样时间间隔有较高的要求。声波在模型中的传播时间为

式中　t——声波在模型中的传播时间；

　h——声波传播的距离，取1.5 m；

　v——声波在模型介质中的传播速度，取均值约3000m/s。

那么，t＝1.5/3 000＝0.000 5 s＝0.5 ms。

要求仪器的采样间隔必须小于0.5 ms，EMS-2型工程多波地震仪的采样时间间隔最小可设置为0.02 ms，因此能够满足测量要求。

（2）测量原理

仪器由震源（锤击或其他方式）激发产生的弹性波经过一定的路径传播到达检波点，检波器的三分量传感器将振动信号转换为相应的电信号，并送入智能采集板的3个对应通道，经多路选择器和两级程控放大器后，进入高精度ADC被转换为数字信号，并存储，等待主机发出取数命令后，发送到主机在高速闪存中存储。信号流程图如图3.3所示。

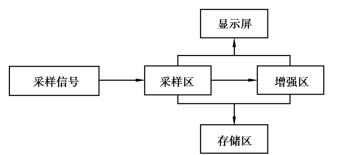
图3.3　信号流程图

测得了岩层的纵波波速和横波波速，就可以用式（3.2）计算出被测模型中的杨氏弹性模量E*、剪切模量G、泊松比μ以及模型的损伤变量等。

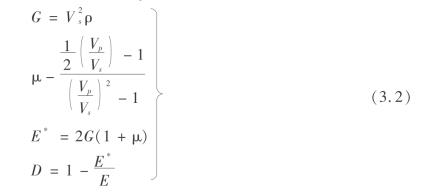
式中　Vs——横波波速；

　ρ——岩体密度；

　G——岩体剪切模量；

　Vp——纵波波速；

　μ——岩体泊松比；

　E*——损伤岩体的杨氏弹性模量；

　E——无损伤岩体的杨氏弹性模量，可用岩石试件在实验室测得；

　D——岩体损伤量。

3.2.2　岩层位移测量方法及原理

位移测量是模型实验的一项基本观测，是进一步分析研究模型对象力学行为的基础。传统的位移测量方法通常是物理测量或机械测量方法。这些方法的缺点有［95］：

①传感器与实验体接触，对实验体的物理性能有一定的影响，安装也比较麻烦。

②传感器的量程有限，只能测量小范围的位移量。

③采样点有限，不能全方位反映模型的位移状况。

④可靠性存在一定问题。

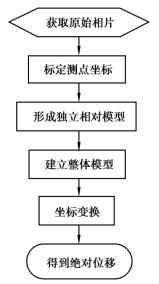
图3.4　数字近景摄影测量过程

因此，本实验采用数字近景摄影测量方式。这种方法是一种非接触式三维测量方法，可以克服传统位移测量法的缺点，并具有测量精度高，方便易行等优点。

（1）数字近景摄影测量的原理［95-99］

数字近景摄影测量过程如下（见图3.4）：将模型初始状态和每步开挖后的状态用数码相机拍摄下来，并转存到计算机上；对每张相片中的各测点进行坐标测量；对相同开挖状态下所拍摄的相片进行各相片间的相对定向，形成各独立相对的独立模型；通过各独立模型的变换进行模型连接，建立统一的整体模型；通过空间相似变换和绝对定向，实现实际坐标的计算，并将初始状态及各步开挖状态下的各测点的坐标统一到同一坐标系中；将每步开挖状态下的各测点的坐标值与初始状态下的坐标值相减，即得到不同开挖状态下各测点的绝对位移。

在进行相片解析以获取位移信息时，当形成立体相对的两张相片的内、外方位元素未知时，可采用单相空间后方交会解算求得其内、外方位元素。当内、外方位元素已知时，可通过相空间前方交会由地面上某点M和相坐标求出其物方坐标，但每张相片均需要5个以上的物方控制点。

相对定向的共面条件为

式中　X1，Y1，Z1——相片1的相点在其相空间坐标系中的空间坐标；

　X2，Y2，Z2——相片2的相点在其相空间坐标系中的空间坐标；

　BX，BY，BZ——相片2的主点在相片1的相空间坐标系中的空间坐标。

将式（3.3）线性化后即可得到用于相对定向的共面观测方程，并通过相对定向形成各相对的独立模型。相对定向不需要按常规方法由左向右依次进行，而是经过判别程序选择最佳组合。这样，设站位置和摄影方向可以任意选择。

相对定向后，通过对各独立模型的变换进行模型连接，建立整体模型。由此所得到的整体模型只是与实体相似，需经过空间相似变换和绝对定向实现与地面坐标的相连。设某点地面坐标为XM＝（XM，YM，ZM）T，相空间坐标为X＝（X，Y，Z）T，则由模型坐标转换为地面坐标的空间相似变换关系表示为

式中　A——由3个空间旋转角所构成的旋转矩阵；

　ΔX＝（ΔX，ΔY，ΔZ）T——3个坐标平移量；

　λ［95-99］——缩放系数。

求解这7个变换参数至少需要7个误差方程式，即在整体模型中有两个空间坐标控制点和1个高程控制点，多余控制点可以提高解算精度。如果实际问题中不需要与地面坐标系连接，则只要1条已知边长和1个已知方向即可完成定向。

图3.5　高解析度数码相机

计算中采用光束法平差，由于误差主要来自镜头畸变和相机的分辨率，所以计算中加入自检校平差，以便对镜头畸变进行修正。

上述相片解析方案使得实地工作时可采用任意方式摄影，大大降低了对作业环境的要求。

实验中使用高解析度数码相机（见图3.5），进行镜头矫正后平均分辨率可达0.1 mm左右。

（2）摄影测量观测误差及矫正

摄影测量观测值的误差一般包括系统误差、偶然误差和失误误差。系统误差主要是由相机本身的镜头畸变误差、镜头保护玻璃偏斜引起的光学误差及用作参照物的小钢尺的刻度误差等引起的。由于像点坐标中包含的系统误差与偶然误差是混杂在一起的，当量测误差较大时，不易对系统误差进行改正。只有当像素点密度较大时，才能有效地进行系统误差修正。

相片的系统误差是相片坐标的函数，对于数码相机而言，不存在相片变形，系统误差主要是由镜头畸变所引起的。一般中、低档相机的镜头畸变都较大，必须通过建立较多的物方控制点来求得镜头畸变参数，本文采用3参数修正模型表示为

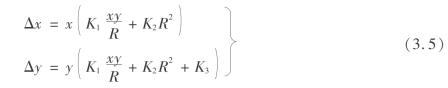
式中　Δx，Δy——镜头畸变产生的修正值；

　x，y——某一测点的像平面坐标值，R＝；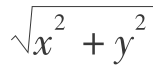

　K1，K2，K3——镜头矫正参数，为常数。

实验中使用的数码相机，经实验测得镜头矫正参数K1，K2，K3分别为0.000 043 12、-0.000 097 81、- 0.017 354 15。

3.3　相似原理及相似准则

3.3.1　相似原理

所谓相似，就是在同一特征现象中，如果表征现象的所有量，在空间相对应的各点和在时间上相对应的各瞬间，各自互成一定的比例［94］。现象相似的性质和被研究的现象之间的相似特征及联系可用相似定理来表示。

相似第一定理：对相似的现象其相似指标等于1。

相似第二定理：设一个物理系统有几个物理量，其中有K个物理量的量纲是相互独立的，那么这个物理量可以表示成相似准则π1，π2，π3，…，πn之间的函数关系式。

相似第三定理：对于同一类物理现象，如果单值量相似，而且由单值量所组成的相似准则在数值上相等，则现象相似。

相似第一定理说明了相似现象具有什么样的性质；第二定理说明了个别现象的研究结果如何推广到所有的相似现象中去；第三定理说明了满足什么样的条件才能实现现象间的相似。

3.3.2　量纲分析法及步骤

量纲分析法是以量纲方程为核心，以方程的齐次性为依据而进行的，其理论基础包括量纲齐次方程的数学理论和相似第二定理即π定理。

若物理方程f（x1，x2，…，xp）＝0共含有p个物理量，其中r个是基本量，并保持量纲的协调性，则可写为

式中　π1，π2，…，πp-r——物理方程中的物理量所构成的无量纲量，称为相似判据。

量纲分析法步骤如下：

①从x1，x2，…，xp中按不同量纲选取r个，组成基本量群。要求这些参数是基本量纲或不能互相导出的量纲，且每个基本量纲在所选的r个物理量中至少出现一次。

②将基本量群中的量纲的幂相乘作为分母。

③将其他没被选入量群的物理量分别作为分子，构成p- r个分式，每个分式为无量纲量，即相似判据π。

3.3.3　相似准则

由于矿山地质条件非常复杂，在开采过程中影响地表沉陷的因素很多，在实验中不可能全面实现。如寻求围岩相对移近量ΔH的函数表达式，在考虑其主要影响因素的前提下，可用函数关系式［101-107］表示为

式中　H——开采层深度；

　L——几何特性；

　E——岩石的弹性模量；

　σ——岩石强度特征，它可以是抗拉、抗压、抗剪强度；

　γ——岩石容重；

　γ′——岩盐容重；

　Q——岩盐支承反力；

　t——总的变形时间；

　t0——岩石蠕变时间；

　η——岩石动力黏滞系数；

　φ——岩石的内摩擦角；

　μ——岩石的泊松比。

按量纲原理，式（3.7）可改写成无量纲的形式为

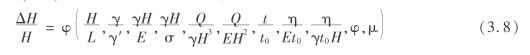
式（3.8）的无量纲化无论在什么测试系统中都应成立。按照相似原理，无量纲化就是相似准则，而模型与原型的相似准则，在数值上必须相等。因此，由式（3.8）可得到相似准则为

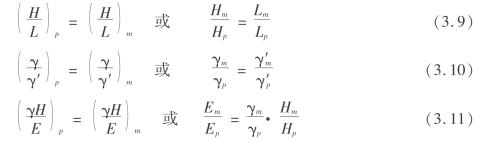
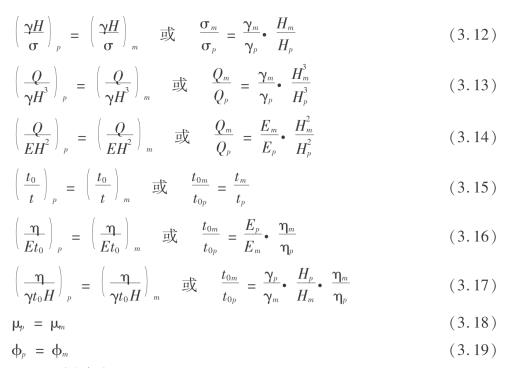
式中　m、p——模型（model）和原型（prototype）。

式（3.9）至式（3.19）表明了模型与原型相似时，理论上应满足的相似准则。然而，在实验中要满足所有的相似准则是不可能、也是没有必要的。只要抓住物理过程的实质，满足其主导相似准则即可。在研究开采沉陷的相似材料模拟实验中，几何相似、动力相似和时间相似是最主要的。本章的实验在考虑边界条件和初始条件的前提下，主要满足几何、动力、时间相似准则。

3.4　相似比的确定

几何比：几何相似，要求模型和原型的尺寸比例为常数，即

常数αl的选择根据研究的问题和实验条件而定，αl确定后，模型和原型所有对应的线性特性之比都应等于此值。本次实验中，αl＝1/300。

时间比：在相似材料模拟实验中，时间比反映了模型和原型运动相似的条件。因原型和模型都在重力场作用下，二者的自由落体运动可用公式表示为

由于重力加速度是相同的，故

即(www.daowen.com)

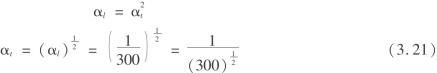
动力比：动力相似要求模型和原型在对应点和对应时刻，所受的力互成一定的比例。在实验中反映力的特征主要是容重和强度。

容重比：从式（3.10）中可得

按相似准则，要求所有的岩层容重之比都相等，即

对于沉积岩层，其容重差异并不大，取其平均容重为γp＝2.5 g/cm3，且选αγ＝0.6，则

γm＝γp·αγ＝1.5 g/cm3

强度比：由式（3.11）有

式中，σ为强度特性，可以是抗拉强度、抗压强度、抗剪强度及弹性模量。按准则，应满足所有的强度特性，但现有的相似材料还没有达到如此高的相似程度，而且根据资料［102-103］表明，只要其主要特征量满足式（3.24）即可。考虑到溶腔顶板的破坏及围岩的变形特性，本实验以岩石的单轴抗拉强度、抗压强度为主要特征量。

3.5　材料配比实验

在相似材料模拟实验中，相似材料的选择是非常重要的，它直接影响着模型实验与原型的相似程度。一般而言，相似模型材料应满足下列要求：

①材料的某些力学性质与岩石相似。

②力学性质稳定，不易受外界条件的影响。

③改变材料配比，可使材料的力学性质有较大的改变。

④模型制作方便，凝固时间短。

⑤来源丰富，价廉且对人体无害。

考虑到这些要求，选择了河沙作为骨料，石灰、石膏为胶结物的混合材料作为相似材料。

在实验室作了材料的抗拉、抗压强度及容重实验，通过对千余块试件进行测试，获得了沙胶比（沙∶石灰、石膏）从4∶1至15∶1的抗拉、抗压强度，实验结果见表3.2所示。

配比号的含义：后面两位是黏结物石灰和石膏的比例，分别用h和g表示，前面的位数是沙的含量，用s表示。那么，混合物总份数为s＋h＋g，其中h＋g＝1。

实验结果表明，随着沙胶比的增大，相似材料的强度减小，拉压比有加大趋势；在沙胶比一定的情况下，调节胶结物的比例也可改变材料强度（见图3.6）；相似材料成型以后，随着放置时间的增长，含水率降低，力学性质随之变化（见图3.7）。

表3.2　相似材料配比实验结果

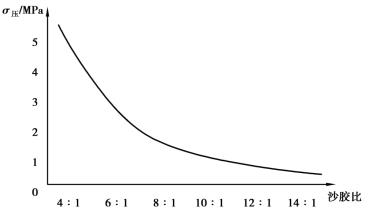
图3.6　沙胶比对抗压强度的影响

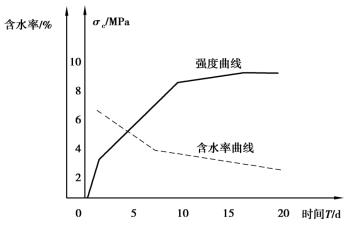
图3.7　相似材料强度与含水率的关系

为了满足动力相似，由式（3.24）和式（3.12）可得

将σp分别代入各岩层的抗拉、抗压强度，即可求出相应的模型材料所需的强度指标，然后从材料配比实验结果中选出满足或基本满足强度指标的材料比例，最后根据模型中岩层的体积、容重和材料比例计算出各分层所需的材料重。各岩层的质量用公式计算为

式中　h——分层厚度，单位cm；

　D——模型宽度，单位cm；

　B——模型长度，单位cm；

　γm——分层容重，单位kg/cm3。

由式（3.25）计算出各分层材料的强度，然后根据表3.2查取配比号。

设相似材料的质量配比为沙∶石膏∶石灰＝A∶B∶（1- B），含水率q＝0.1，那么每个分层材料的质量计算：

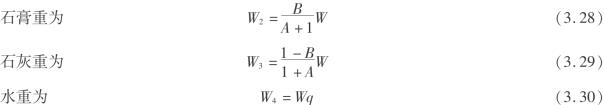
计算结果如表3.3所示。

表3.3　模型实验材料配比表

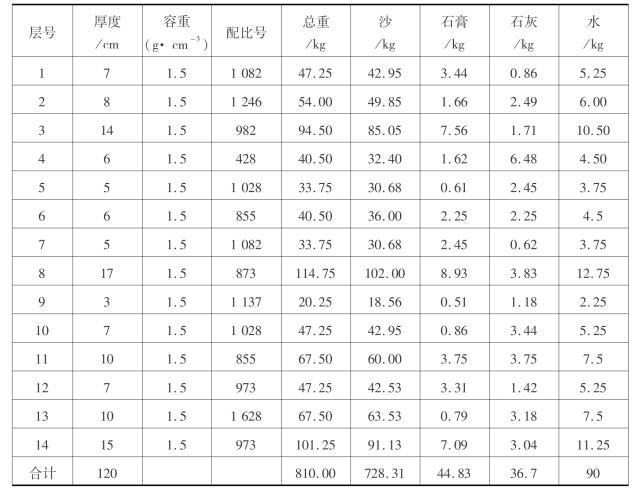
3.6　模型制作

模拟实验台兼作模具。制模时，前表面用木板封闭，木板上标注好每一层岩层的厚度。按表3.3所示的配比称好各材料的质量、搅匀，逐层装入模型架中，并夯实到标注的刻度。在层理间加入适量的云母粉和滑石粉模拟自然层理，并在每一分层中加入少量云母片模拟初始节理、裂隙等弱面。装入材料的同时，后表面的木板也随着材料增高逐渐封闭。为了减少摩擦，在模型架的两边分别放置塑料薄膜。等材料全部上完后，在模型前后用角钢固定，防止模型前后表面产生膨胀。

3.7　水的处理

模型实验中，因为考虑到模型的稳定性及材料的特性，以及岩盐溶腔顶板破坏主要是以拉伸破坏为主，顶板受上覆岩层的质量和溶腔水压作用，可将顶板载荷简化为上覆岩层质量与溶腔水压之差，将溶腔水压换算成采深。因此，不模拟溶腔内的水压。

3.8　开采及测量

根据实验目的及地区的气候，本实验采用湿模型法作模型实验。在模型制作完成后的3～7天，拆去前后模板，测定模型材料的含水率，当与材料配比实验的含水率相符合时，即开始开采和测量数据。

按时间比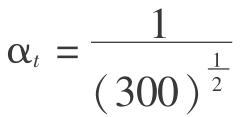＝1/17，则84 min相当于实际的24 h。如果每天开采一次，即84 min进行一次开采。

假设岩盐水溶开采，溶腔几何形态近似于倒圆锥体，在平面模型上为倒三角形。按αl＝1/300，实验一次掘进2.5 cm，45度的溶蚀角，共开挖8次，挖完整个厚度，然后再向两边平行推进，昼夜实际开采7.5 m。开采推进过程如图3.8所示。

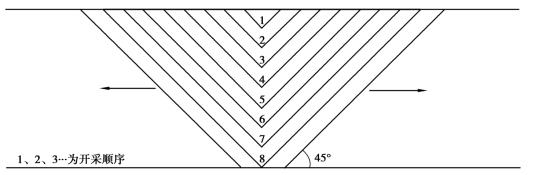
图3.8　开采推进过程

在模型上覆岩层中总共布置13行测点，每行9个测点，共计9×13＝117个。测点设置如图3.9所示。

采用摄影系统摄制整个开采过程；每次开挖前用高清晰度数码相机拍摄模型并用地震仪测量岩层力学参数和损伤量。

数码相机固定在三脚架上，使用电脑软件控制进行拍摄，确保每次拍摄时，相机位置固定。

岩层波速测试采用声波透射法，在每层岩层的两端，一端进行声波发射，另一端进行声波接收。声波发射采用锤击法，用小铁锤敲击声发射点。发射和接收示意图如图3.10所示。从开挖开始就对每层岩层的损伤量进行测量；直到某层岩层发生明显破坏和断裂时，终止对该层岩层进行测量。

图3.9　位移测点

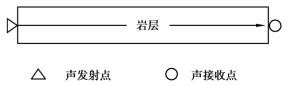
图3.10　弹性波透射法测试

3.9　实验误差及修正

研究表明相似材料模拟实验研究开采沉陷的误差主要表现在相似性误差、边界条件误差、相似材料配比误差、模型自重压缩引起垂直沉降误差和模型边界开裂引起的水平移动误差等［92］。

其中相似性误差主要表现在时间比αl＝α2t，研究表明上式确定的时间比例，未考虑相似材料与实际岩层的强度、变形破坏性质等，故存在一定的片面性。另外，由于材料随时间变形的理论研究不足，时间比例αt还难以用一个确切的式子加以表达。因此，不可避免地引起时间相似误差。

动力学相似要求模型与实型间所有作用力保持相似，即满足牛顿数为

式中　Rm——相似材料力学参数；

　RH——岩石力学参数；

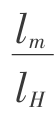　——模型比例尺；

　——相似材料与岩石的容重比。

材料的力学性质包括抗压强度、抗拉强度、抗弯强度、黏聚力、内摩擦角等。模型实验中仅选择抗压强度和抗拉强度作为动力学相似指标，因而只能近似地达到整体力学性质的相似。同时，岩石作为特殊的固体材料，是由多种矿物晶粒、孔隙和胶结物组成的混杂体，经过亿万年的地质演变和多种复杂的构造运动，从本质上形成了岩石结构从宏观到微观极其复杂的非连续体和非均质体，由实地采集岩样测试获得的强度指标一般不能全面反映岩体的整体强度，而模型强度指标的确定是以岩石强度指标为依据，不可避免地形成模拟强度的误差。

边界条件误差：覆岩与地表移动问题属于结构纵深很长的工程问题。根据弹性力学平面问题的划分，在实型中截取其中的一片来研究。可将其归类于平面应变问题。对于平面应变，则有εy＝0，σy＝μ（σx＋σz）≠0；而相似材料模型则可看成是等厚度薄板形式的弹性体，可归类于平面应力问题。对于平面应力，则有σy＝0，εy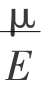＝-（σx＋σz）≠0。可见模型与实型分属于平面问题中的平面应力和平面应变两种类型，两者间边界条件的不符，在一定程度上降低了两系统间的相似性，由此必将引起模型的实验误差。

相似材料配比误差：研究表明，模型湿度变化将引起模型材料强度变化，导致模型与实型力学条件的相似误差。此外，由于材料来源不同，其性质可能有所差异，诸如河沙的级配不同或混入的杂质不同等，也能引起相似材料强度值偏差。这些在实验中难以控制，不可避免地导致误差。

模型自重压缩引起垂直沉降误差：随着模型的铺设，上覆岩层载荷的增加，将导致下位岩层产生压缩。这一压缩量将导致垂直沉降误差。

模型边界开裂引起的水平移动误差：模型实验中模型两侧开裂不仅与模型本身的干燥收缩有关，也与模型的开采、岩层倾角、地表形态等有关，且以开采影响为主。开采将导致模型地表以下、中轴线以上部分受压缩，中轴线以下受拉伸，如图3.11所示。拉伸、压缩的结果使模型两侧岩体失去平衡产生转矩，导致模型两侧出现楔形开裂，使水平移动产生误差。

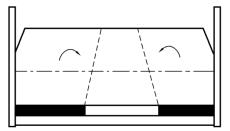
图3.11　模型边界开裂示意图

其中，相似性误差和边界条件误差，目前还不可避免；相似材料配比误差可以通过改善实验条件来消除；模型自重压缩引起垂直沉降误差和模型边界开裂引起的水平移动误差可以进行修正［92］。

模型自重压缩引起垂直沉降误差修正：随着模型的铺设，上覆岩层载荷的增加，将导致下位岩层产生压缩。假设第i层模型材料的厚度为hi，弹性模量为Ei，容重为γi，则上覆载荷引起的第i层岩层的压缩量为

上覆岩层自重载荷引起的第i层模型材料的压缩下沉总量为

如果假设E为模型材料的平均弹性模量；γ为模型材料的平均容重；H为模型高度，则在模型深度为z的水平上产生的压缩下沉为

从而可得

式中　k——模型常数，。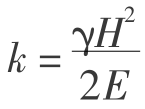

可用式（3.34）对沉降量进行矫正。

模型边界开裂引起的水平移动误差修正：如图3.11所示，拉伸、压缩的结果使模型两侧岩体失去平衡产生转矩，导致模型两侧出现楔形开裂。其偏角公式为

式中　J——惯性矩；

　c——积分常数；

　M（x）——转矩。

为讨论方便，取M（x）＝m＝常数，由边界条件Q（x）x＝l/2＝0，可得

式中　l——模型长度。

由式（3.36）可知，偏角是坐标x的线性函数。而地表铺层的水平位移与其偏角成正比，由此可得水平位移修正也是坐标x的线性函数。为此，只要量出模型两侧开裂的水平宽度，就取得了水平移动的最大改正值。按线性关系确定模型边界到模型地表中部所有测点的水平移动改正值。

3.10　实验结果及分析

实验中建立了两种模型，模型1在分层间没有添加云母和滑石；模型2在分层间加有少量云母和滑石来模拟层理。两种模型的其他情况完全一致。

模型1总共进行了25次开挖，开挖宽度为187.5 m。当溶腔顶板跨距为45 m时，溶腔顶板开始出现裂隙，裂隙高度为3.0 m；当溶腔顶板跨距为90 m时，顶板上有部分小块剥落；随着跨距的增加，顶板裂隙带增宽；当溶腔跨距为187.5 m时，顶板失稳垮塌，垮塌高度54 m，宽度90 m。至此，溶腔报废，不再进行开挖。在整个开挖过程中，上覆岩层中没有离层出现。

模型2总共进行15次开挖，开挖宽度为112.5 m。当溶腔顶板跨距为30 m时，溶腔顶板开始出现裂隙，裂隙高度为2.5 m；当溶腔顶板跨距为60 m时，顶板上有部分小块剥落，上覆岩层出现离层，离层位置在顶板上51 m处；随着跨距的增加，顶板裂隙带增宽；当溶腔跨距为112.5 m时，顶板失稳垮塌，垮塌高度34 m，宽度60 m，并且在顶板上81 m处产生离层。至此，溶腔报废，不再进行开挖。

由于模型1的岩层间没有加云母和滑石模拟层理，致使整个上覆岩层胶结为一个整体。因此，其模拟结果与实际情况有很大的差别。以下的分析都以模型2的测量数据进行。

3.10.1　岩层损伤演化过程

在实验过程中，从开挖开始就对每层岩层的损伤量进行测量，直到某层岩层发生明显破坏和断裂时，终止对该层岩层进行测量。

表3.4所示为模型2每次开挖的岩层损伤量数据表。

表3.4　开挖过程中岩层损伤量演化表

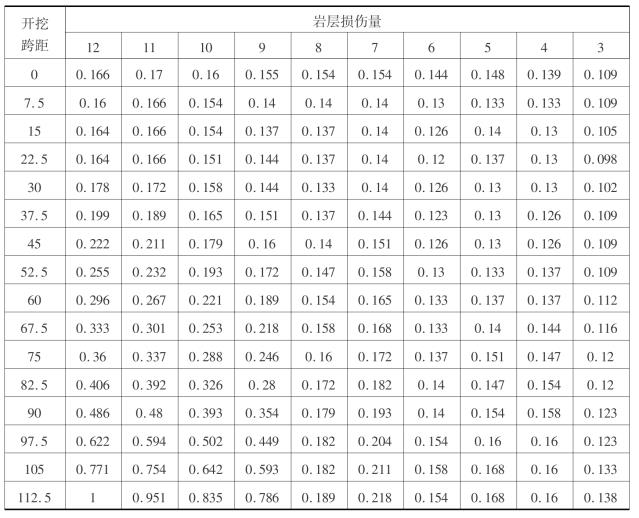
将如表3.4所示的数据作在以开挖跨距为横坐标，损伤量为纵坐标的坐标轴上，可得到上覆岩层开挖影响的损伤演化曲线（见图3.12）。

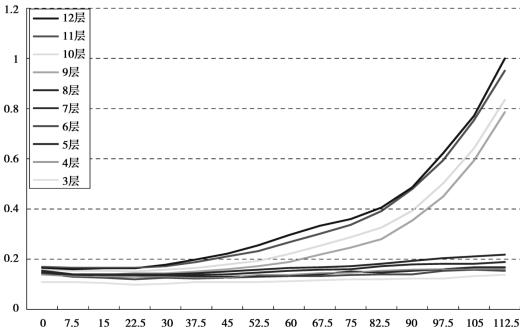
图3.12　上覆岩层损伤演化曲线

由图3.12所示可以明显地看到，第12至第9层岩层产生了较为严重的破坏：其中第12层岩层完全破坏垮塌；第11层岩层部分垮塌，剩余部分严重破碎；第10、第9层岩层也破碎严重基本失去承重能力。第8以上各岩层受影响较小，没有产生明显的破坏情况。在第9和第8岩层间可以十分明显地看到离层现象。由岩层力学参数可知，第8层岩层较厚，强度较高，在其下部岩层失去承载能力时，它能够对上部岩层提供支撑力，而不产生较大的破坏情况。

从破坏严重的岩层损伤演化曲线可以看到，岩层的损伤演化基本可以分为3个阶段：第1个阶段，岩层损伤量基本保持不变，甚至可能因局部应力增大而导致损伤变小的可能；第2个阶段，岩层损伤量以一定的斜率保持稳定而缓慢地增长；第3阶段，岩层损伤以指数函数形式加速增长，很快导致完全破坏而失去承重能力。实验中第12至第9层岩层损伤演化达到了第3阶段；而第8以上各岩层基本处于第2甚至第1阶段。

对第12至第9层岩层损伤演化数据进行回归分析，可以得到由开挖跨距为变量的岩层损伤演化方程为

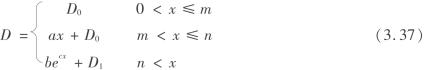
式中　D0——岩层初始损伤量；

　D1——第2阶段的最大损伤量，D1＝an＋D0；

　a、b、c——回归参数，随岩层不同而改变；

　m——岩层进入第2损伤阶段的跨距值；

　n——岩层进入第3损伤阶段的跨距值。

3.10.2　岩层移动变形

为了观测岩盐开采后上覆岩层及地表的位移情况，在每层岩层上，都布置了位移观测点，如图3.9所示。定义观测点的序号为，从左上角的测点序号为1，水平向右一直到9，然后从左边开始第2行，依次编号，直到右下角，共117个测点。实验总共进行了15次开挖，每次开挖后进行位移测量，测量方法采用近景数字摄影法，获得每次开挖后所有测点相对于初始状态垂直和水平方向的位移值。以下是模型2的上覆岩层位移分布特征：

对最终状态拍摄的图像进行处理后获得了所有测点垂直方向和水平方向的位移值，表3.5列出第1、4、8、9、11层岩层上的测点位移。将这些测点值进行插值后，分别绘制成垂直方向和水平方向的岩层位移曲线图（见图3.13、图3.14）。

表3.5　部分测点x、y方向最终位移量

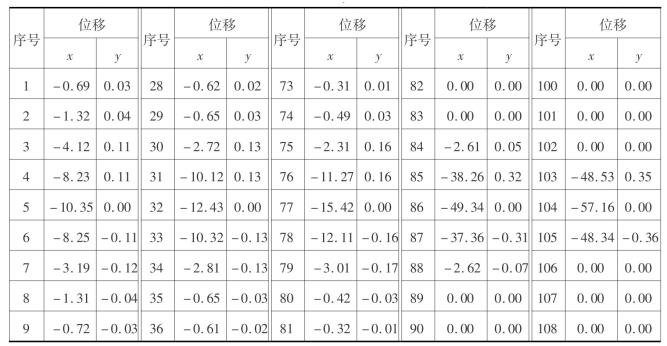
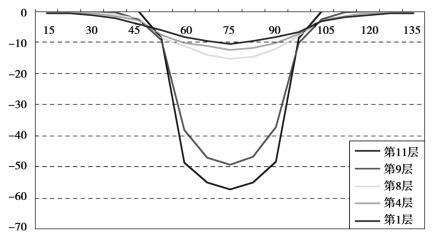
图3.13　模型岩层垂直位移

对于垂直位移，可以看到：垂直位移随上覆岩层距岩盐层垂直距离的增大而减小，同时距岩盐层越近的岩层，其垂直变形越集中在中间小范围内，而两边几乎不会发生位移变化，比如第11层岩层只在60～90 cm范围内产生了垂直变形；相反远离岩盐层的岩层其垂直位移减小，但移动范围增大，比如第1层岩层几乎整体都产生了垂直位移。在同一水平层上，距盐腔中心的距离越小，其垂直位移越大。

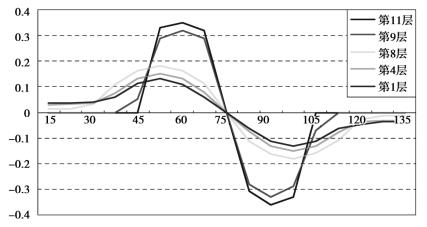
图3.14　模型岩层水平位移

水平位移几乎有同垂直位移类似的规律。只是其变形量是集中或分散在溶腔中心点两旁的。

不难看出，位移量越小的岩层其变形范围越大；反知位移量越大的岩层其变形范围越小。

位移图上明显反映出了岩层岩性对岩层变形的影响。第8层岩层位移曲线和第9层岩层位移曲线有明显的区别。而第1、4、8层岩层的位移曲线则差别不大；第9、11层极为相似。说明第8层岩层和第9层岩层间的位移变化并不连续，出现了离层。这和岩体损伤分析结果一致。

3.10.3　开采沉陷的层面效应及分层特性

上覆岩层是岩性相差很大的许多层岩层按一定的顺序沉积形成的，在岩层之间一般都存在着弱面（层理），层理对开采沉陷的影响很大。最为明显的就是离层的产生。在离层产生处，层理不但发生了法向位移，同时也发生了较大的切向位移。这一点从模型的岩层移动变形图上可以清楚地看到。层理承受抗拉和抗剪的能力都很差。因此，层理的存在，在一定程度上改变了上覆岩层的整体刚度，使整个上覆岩层相当于由多层相互独立的单一岩层直接堆砌而成。这样，在相同采动条件下，弱面抗拉、抗剪能力越弱，则地表移动变形就越大。这一点可以从两个模型的岩层移动变形值可以明显看出。在相同开挖跨距时，模型2的变形比模型1明显要大一些。上覆岩层的层状结构，决定了上覆岩层的移动变形具有分层特性，上覆岩层不会作为一个整体进行变形、移动和破坏。

3.10.4　岩层破碎岩体尺寸特征

按简化两端固支梁理论，由式（2.22）可知有，岩层最小破坏尺寸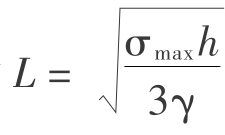，岩层破碎岩体尺寸与岩层强度、容重和垮塌厚度有关。图3.15所示是岩层初次垮塌时的过程。从图上可见，顶板垮塌前出现微小离层，然后岩层从顶板两帮断裂垮塌。此现象与简化两端固支梁理论相同。因此，实验现象验证了岩体初始损伤影响开采沉陷的力学机制，同时也证明了岩层垮塌尺寸是由岩层强度、容重和垮塌厚度决定的。

图3.15　岩层初次垮塌过程