本章主要研究城镇化发展的微观基础：集聚—扩散机制，它是经济活动运行的前提和基础。本章的研究仍然侧重于理论分析，以介绍理论模型为主，同时通过空间计量模型进行实证检验，表明区域经济增长带有明显的集聚趋势。后面的章节会就相关内容展开论述，并作相应的实证研究。

集聚机制是指在集聚效应（极化效应）的作用下，包括人口在内的各种经济要素在地理空间上表现为向某一位置集中和聚合的趋势；扩散机制是指在扩散效应（涓滴效应）的影响下，经济要素由分布密集的中心地向周围地域空间扩展和分散的趋势[1]。集聚效应起源于马歇尔（Marshall，1890），主要来源于规模经济所产生的正的外部性，规模经济是城市经济理论的重要特征，其产生的原因常被解释为：劳动力共享、专业化投入和知识溢出。企业在城市中集聚能够面对面交流信息而降低各种各样的交易成本。此外，消费者也比较容易获得各种各样的差别化产品。这种正的外部性使得企业和消费者在城市集中。同时，在城市经济活动中也有与集聚相对立的力量，过度集中在大城市会产生负的外部性，如污染、长距离的交通成本以及土地稀少而带来房价和租金飙升等。城市空间集中度是由集聚力和扩散力的均衡来决定的。一些重要的因素也会对集聚和扩散作用施加影响，其中一个最主要的因素是运输成本，它会随着科技进步和交通条件改善而降低。事实上，当农村地区人口流失，工业革命以后大城市纷纷涌现，20世纪70年代以后许多发达国家城市集聚已经停止或者说扩散现象开始发生。假如运输成本随着时间降低，在下降的运输成本和空间集聚之间存在一个“U”型关系。也就是说，在运输成本非常低或者非常高的时候扩散发生，处于中间水平时集聚发生。（Helpman，1995；Krugman和Venables，1995；Venables，1996；Puga，1999）一般来说，在城市集聚的最初阶段，集聚的经济效果明显，集聚不经济影响微弱；但城市空间达到一定规模之后，集聚不经济影响逐步增强并抵消集聚经济的正效应，直到最后完全抵消。因此，集聚经济利益在开始阶段随着城市空间规模的扩大而不断增强，达到一定规模后又呈现出递减趋势，直到最后可能降为零，从而使城市吸引力基本消失，城市的空间规模不再增长。（谢永琴，2006）上述研究解释了集聚和扩散的机制：当运输成本足够高时，企业就会分散到各地满足对最终产品的需求；当运输成本处于中间，企业就会集聚在一起分享外部性带来的前向—后向关联；然而当运输成本下降足够多，集聚不再重要，因为与其他企业或消费者接触非常容易。

集聚—扩散机制贯穿于区域经济发展的整个过程，集聚主要导致区域局部地区的快速增长，而扩散则带来整个区域的经济发展。笔者认为，扩散机制发生作用的原因除了规模不经济以外，还包括知识溢出。因为知识溢出是外部性的潜在力量。城镇化被认为是通过促进集聚获得收益，如本地化信息和知识的溢出效应，从而推动经济增长。（Henderson，2003）如果将负的外部性产生的扩散看作被动扩散，则由知识溢出所产生的扩散就是主动扩散。因为现实当中知识可达性对城市体系的发展演化具有非常重要的影响。

集聚经济是推动城市形成和发展的直接动力，城市集聚产生规模报酬递增是进一步加强集聚的动力。城市体系可以看作一个整体，它是由内生的大量不同规模的城市构成，而每一个城市内部又具备了“中心—外围”结构。作为单独的城市，其发展过程也是一个“集中—分散”的过程，中心和外围之间的关系也是先趋异后收敛。一开始受集聚力的影响，产业和要素向中心地区集中，在马歇尔外部性的影响下有了知识的创新和积累，进一步提高了中心地区的劳动生产率和技术工人的人力资本。随着知识资本的不断积累，加上劳动力要素的流动产生知识溢出效应。虽然通信科技不断发展，网络广泛普及，信息传递的运输成本逐步降低，但是知识和技术的传播仍然不能摆脱区域的限制，主要由于：一方面，知识溢出和溢出方与接受方的距离有关，这是因为知识的溢出效应随着距离而衰减（距离上海近的城市受上海知识溢出效应的影响远远大于受杭州的影响，同样与杭州距离近的城市受杭州的影响远远超过受上海的影响），同时应该注意到有些知识和信息，特别是那些无法符号化和规范化表述出来的默会知识[2]，必须通过面对面接触和交流才能传递，即使要跨区域传播也需要十分漫长的过程。另一方面，知识溢出主要和接受方的吸收能力（包括人力资本、制度环境、教育水平等方面）有关。距离近但是吸收能力弱的地区受知识溢出效应的影响也未必强。根据知识可达性来衡量，知识溢出效应空间范围的大小直接决定着技术知识对区域经济增长的贡献。知识能够容易到达的地区，经济会增长较快，经济发展带来人口的集中，城镇化水平也会相应提高。因此，知识的溢出和扩散将有助于缩小中心与外围地区的差距，使区域经济发展走向平衡和收敛。

在城市体系中，知识由单个城市的中心首先向该城市外围溢出，使城市整体发展水平提高，城市内部的差距减小。接着知识再向以这个城市为中心的外围吸收能力强的地区溢出，推动该地区的经济增长并提高它的集聚水平，使城市与城市之间的差距缩小，向平衡化方向发展，这同样适用于协调地区与地区之间的发展。在极化条件下，中心地的集聚主要包括人力资本、资金、生产要素、产业。集聚通常发生在基础设施条件比较好、城镇化水平比较高的城市，这又为进一步的知识和技术创新创造必要条件；中心向外围的扩散是由于很多学者认为的过度集聚带来的规模不经济，在负的外部性的压力下（地价上涨、劳动力成本提高）使产业和生产要素向外围扩散。这反映了区域经济发展自我协调的趋势和过程，作为政策制定者不可能被动地等待出现过度集聚状况或者当规模不经济发生作用后，由经济主体自己组织实现均衡。实际上在未达到过度集聚的临界点之前，知识溢出效应已经开始生效，并且信息和知识作为高级生产要素不受到极化作用力的影响，而是先由近及远向外围地区扩散，它们也是推动其他要素进一步扩散的原动力，贯穿于集聚和扩散的整个过程。因此，解决区域协调发展（包括区域内和区域之间）问题的有效途径是建立有效的知识传导机制，加强培育落后地区的知识吸收能力。

在研究城市集聚—扩散模型当中，亨德森（Henderson，1999，2005）研究了城市增长模型，重点集中在城市的形成、内生增长对城市规模和数量变化的影响等方面。在亨德森的模型中为了避免集聚不经济，同时又分享制造业集聚的地方化效应[3]，简单而又极端的假设就是令城市之间和区域之间的运输成本为零，于是均衡条件下一个城市只能生产一种商品，但这是不现实的。同时，在克鲁格曼（Krugman，1991）的模型当中，跨区域的运输成本为正，而忽略了城市之间的交通成本，得出了与亨德森模型相反的结论，即每一个企业都生产多样化产品并集聚在一起避免跨区域的交通运输，这是形成城市集聚的最主要原因，也是实质性的扩展，但是由于忽略了城市之间的运输成本，仍然不现实，这两种模型都属于比较极端的情况。田渊（Tabuchi，1998）把这两种模型统一起来，假设城市之间和城市内部都是正的运输成本，提出了一个关于亨德森模型和克鲁格曼模型的合成理论。借助这个合成模型，考察企业和工人在区域之间集聚和分散的原因。此模型在克鲁格曼模型的基础上加入阿隆索（W．Alonso）模型中对土地的消费，进一步考察土地市场的价格机制对城市集聚和扩散的影响。

在田渊（Tabuchi，1998）模型中有两个区域，每一个都包含一个CBD中心，周围空间都是没有什么特色的平原，同质性的工人都住在CBD周围并往返于之间，生活在区域k的某工人的效用函数表示为：

其中，cik是区域k对商品i的消费，CSk是区域k住房空间的消费，CAk是区域k对农产品的消费。假定农产品运输无成本，农产品价格是由国际市场决定的，是标准计价物。参数μ和γ是正的，且μ＋γ＜1，σ是替代弹性，σ≥1。有N种不同的商品，使用CES效用函数暗示了工人喜欢产品多样化。用萨缪尔逊的“冰山”模型反映跨区域运输成本，一单位的货物中只有τ部分（τ∈［0，1］）能到达另一个地方。换句话说，商品的到岸价格是离岸价格的1／τ倍，如果pik是区域k（k＝1，2）商品i的离岸价格，则商品i在另一个区域的到岸价格是pik／τ。

假定区域k有Nk个企业，那么在区域1的工人的收入限制是：

其中，x是到CBD的距离，r（x）是在地点x的住房租金，T（x）是交通成本的一般表达式，w1是区域1的工资率，区域2的收入限制的定义也是类似。交通成本是随距离而增加的。工人从土地所有者那里租房子，他们保持着租金收入。在方程（5－2）的收入限制条件下，针对cik最大化方程（5－1）的效用得到：

把所有的人口总数定为1，每个地区农民的数量固定为（1－μ）／2，区域k制造业工人的数量是Lk，L1＋L2＝μ，农民几乎是不移动的，制造业工人根据两个区域的效用差别来自由移动。制造业生产单个差别化商品i的成本包括一个固定成本和一个固定的边际成本，为lik＝α＋βcik。其中，lik是区域k生产商品i的劳动力投入，cik是区域k生产商品i的产出。每一个企业根据价格pik最大化其净利润pikcik－wk（α＋βcik）。假定在垄断竞争市场的固定替代弹性为σ，则一阶条件下得到：

此外，假设企业可以自由进出，且均衡条件下利润为零。在收入限制条件方程（5－2）下针对ck，CSk和CAk最大化效用方程（5－1）得到μ［w1－T（x）］＝N1p1c1＋N2p2c2／τ，将这个方程结合方程（5－3）、（5－4）和ck。因此，CMk能够通过wk、T（x）和参数表示，将CMk，CSk和CAk代入到方程（5－1）的效用函数并计算x＝xk（土地租金都等于每一个城市边界的租金）时，得到效用比率方程（5－5）：

其中，xk是CBD到城市边界的距离，f≡L1／（L1＋L2）∈［0，1］。在城市边界，土地租金满足农业租金rA无论在哪里都是固定的，因为农产品的运输成本为零，定义r（xk）＝rA。当方程（5－5）等于1时，实现长期均衡。

住房的土地消费，在克鲁格曼（Krugman，1991）的模型当中缺失。在单中心城市，每个消费者在收入限制条件下满足农产品、工业产品、居住空间和地点等方面的效用最大化。根据一阶条件，得到著名的区域均衡条件：

此方程意味着在任何地点x上的土地租金支出的边际变化被交通成本的边际变化所抵消，通过一阶条件除去变量ci和CA得到：

从这两个方程可以得到：

租金曲线被给定为：

其中，r0是CBD的租金，确信土地租金随着到CBD的距离增加而递减，位于x地点的人口密度假定为人均居住空间的倒数：

介于x和x＋dx的人口是2πxdx／Cs（x），把这个区域积分得到城市人口。因为城市人口等于区域k制造业工人的数量，则可以得到制造业工人的均衡数量：

其中，方程（5－8）是由方程（5－6）和（5－7），用xk代替x且rA代替r（xk）得到。

此时，每个区域所有收入为：

其中，φk被定义为可支配工资占总工资的比重，可支配工资是总的工资扣除交通成本，介于0和1之间。按照克鲁格曼的模型把z1k定义为区域k（k＝1，2）在区域1商品的支出与在区域2商品支出的比重，使用方程（5－3）和方程（5－4），z1k可以写成：

区域k工人的所有收入等于两个区域的所有消费者对区域k所制造商品的消费支出：

方程（5－12a）的等号右边是区域1所有制造业商品的消费，方程（5－12b）的等号右边是区域2所有制造业商品的消费。令方程（5－5）等于1并且把方程（5－10）中的φk代入方程（5－9），通过一系列的方程求解变量f、xk、wk、Yk 和z1k（k＝1，2），由于方程都是非线形的，很难求出具体解的表达式。

接下来主要考察区域之间交通成本τ对于城市体系结构的影响。由于方程体系的复杂性，以下分析讨论几种极端情况的结果：交通成本无限大（τ＝0）和交通成本为零（τ＝1）。由于跨区域交通成本随时间降低，低τ对应于古代，高τ对应于现在。特别是要检验城市集中、扩散均衡的稳定性，稳定的均衡意味着任何企业离开到其他城市都不可能得到更多收益。

1）τ＝0交通成本无限高，每个城市都倾向于自给自足

城市集中即是稳定均衡。方程（5－13）表明在运输成本很高的情况下（如τ→0），当替代弹性σ非常小或者制造业就业比重μ非常高时，企业集中。前者意味着当制造业商品之间的替代弹性非常低而交通成本非常高时，在小城市的居民效用就会非常低，因为购入不可替代商品的成本太高，所以生活在大城市有各种各样的商品可供选择而变得更有吸引力。后者μ非常高的理由更加直接，当制造业比农业更重要时当然会形成集聚。

此时γ＝1／2，扩散即是稳定均衡。当跨区域交通成本非常高，在古代区域之间没什么交通工具，每一个城市都是独立的自给自足经济，城市规模的分布取决于农民的分布规模，最初的替代弹性σ非常高且制造业就业比重μ非常低。

2）交通成本为零（τ＝1）

当跨区域交通成本为零，城市之间完全的经济一体化，对应于现在和将来跨区域交通变得非常便利，扩散对于任何初始状态和任意参数都是城市体系的稳定均衡状态。由于技术进步跨区域运输成本可以忽略，将来城市集聚会停止，企业和工人会分散。没有集聚的必要，分散使消费者享受更多的土地消费和短时间的往返。这种情况同样适用于信息服务产业，通过互联网跨区域的信息传递相当于跨区域的货物传递，就像交通工具的技术进步一样，通信方面的技术进步同样也使城市活动向外扩散。

集聚—扩散机制在区域经济发展的不同阶段起的作用不同，在时间上集聚起主导作用先于扩散起主导作用。集聚促进城区与郊区互动，在中心城镇化阶段发挥主导作用。在中心城镇化阶段，区域内的各种资源、人口、产业、交通基础设施等不断由区域相对分散的均衡状态向区域内个别条件稍好的经济核心集中，这些条件稍好的经济核心，事实上是区域内最早出现的城区。在一段时间内，由于城区土地利用空间巨大没有出现“城市病”，城区人地关系和谐，集聚会保持下去并促进城区空间进一步扩张，同时伴随着其势能不断提高。当城区用地紧张、人口容量超载、企业经济效益下降等“城市病”出现时，扩散开始逐渐发挥主导作用，这一阶段也就是郊区城镇化或逆城镇化阶段。在这个阶段中，城区用地紧张、人口超载、劳动力成本上升，许多加工制造业发展受限，迫使人口居住区向郊区扩散、加工制造产业到郊区重新选址以谋求新的发展空间。需要说明的是，不能简单地说在中心城镇化阶段，城区与郊区的互动中仅存在集聚力量，在郊区化或逆城镇化阶段仅存在扩散力量。事实上，在中心城镇化阶段，在城区与郊区的互动中也存在着扩散，这时的扩散表现为城区发挥城市的基本职能，即城区向郊区提供商品和服务，带动郊区的发展；在郊区城镇化或逆城镇化阶段，同样也存在集聚，这时集聚遵循市场经济的基本规律，对资源进行优化配置。

新型城镇化相对于传统城镇化而言，突出的是城乡统筹和大中小城市、小城镇协调发展。既要加快发展一批具有影响力、带动力和竞争力的大城市，强化大城市的产业支撑，充分激发大城市的集聚和辐射能力，又要推进那些工业基础较好、交通便利、综合承载力较强的中小城市发展，强化其与大城市的经济联系；既要发展新型工业化又要改造传统农业，转变农业增长方式，加快农业现代化发展。在新型城镇化过程中，农村生产力得以充分释放，农村大量的剩余劳动力进入非农生产部门成为产业工人，人口的集中带动产业的集聚和服务业的发展。杨开忠（2001）认为劳动迁入将增加城市劳动力供给和地方支出，因而抑制城市工资上升，增加生产规模报酬，进而提高城市生产率，增强城市盈利能力。这将导致城市积累能力提高和新的资本形成，新资本的形成吸引劳动力迁入，而劳动力迁入又将增加城市地方支出。从农户角度来看，所谓农业产业化就是农户专门经营农业价值链中某一个或某些增值活动，其他增值活动逐步市场化的过程。农村劳动力流入城市将使农户自身经营农业增值活动的预期机会成本上升，农户倾向于减少自己经营农业增值活动的范围和规模，增加从市场上购买农业增值服务的范围和规模，从而扩大农业增值服务的市场，拉动农业产业化。农业产业化将推动农业的规模化、专业化和农产品科技含量大幅度提高，一方面推动农业产出增长并且农业劳动力和土地进一步向城市转移，进而促进城镇化发展；另一方面降低了农户通过市场获取农业增值服务的价格，从而反过来推动农业产业化发展。大城市集聚了包括文化知识、技术创新和社会资本等在内的高端生产要素，具有资源比较优势的城市在集聚效应的作用下快速发展起来，同时也拉大了与周边城乡之间的差距。随着统筹城乡一体化的推进，阻碍城乡人口流动壁垒的消除，城乡在交通、通讯、互联网、教育、培训等领域都逐步实现了一体化，为城乡之间生产要素的自由流动创造了条件。那些经济发展水平高的中心城市以空间和产业为途径将资本、人才、技术、市场、信息、思想观念、生活方式等向周边地区扩散，使农民在生产、生活方式发生改变的同时整体素质明显提升。在现有的城市体系中，小城镇是城市与农村的政治、经济、文化的连接体和中转站，它是城乡之间人流、物流、信息流传递转换的重要桥梁和纽带。有重点地发展小城镇，引导农村人口和产业向条件较好的小城镇集中，培育优势特色产业，提高小城镇人口的集聚规模和公共服务能力，进一步发挥小城镇的承载、承接作用是统筹城乡一体化发展的有效途径。浙江省针对一些中心镇发展面临的集聚辐射能力不强、基础设施和公共服务滞后、要素制约突出等问题，于2010年作出开展小城市培育试点的战略决策，确定了27个小城市培育试点镇[4]，通过把中心镇培育成小城市作为推进新型城镇化、促进城乡统筹发展的重要载体。

集聚和扩散是城市群空间发展最重要的理论之一，也是城市群地域结构演化的重要动力机制（朱英明，2001）。我国正处于工业化、城镇化加速发展阶段，城市群空间体现出集聚与扩散共同推进的循环往复过程。首先是单个城镇区域不断扩展、区域城镇个数不断增多并向着核心城镇集中，在空间上表现为城镇的集聚，城市群开始出现。随着城市群区域内城镇的质量优化和数量攀升，城市群的内涵式和外延式扩展持续进行，在空间上表现为城镇的扩散，整个区域的城镇化水平达到均衡状态；与此同时，在一个较高的起点上，区域开始新一轮的发展（彭翀和顾朝林，2011）。美国区域发展与规划专家弗里德曼（J．R．Friedman）依据工业化水平将区域经济发展划分为四个阶段并对其空间特征进行了深入的研究。基于其研究成果，区域空间基本上历经低水平均质化—极核化—点轴化—均衡化—一体化的演进过程。在工业化中期阶段表现为区域空间组织构架、点轴系统形成，集聚因素作用强烈，区域不平衡扩大；在工业化后期及后工业化阶段，区域空间组织构架、点轴系统进一步完善，等级差别缩小，集聚因素作用减弱，区域不平衡缩小，区域组织以均衡化、网络化、等级规模合理化为特征；等等（李慧中和王文海，2007）。

以服务业为主的第三产业在城镇化水平比较高的地区集聚，在原来的城市群中产生以中心城市为代表的增长极，在中心城市极化作用的影响下，城市群开始向“都市圈”演变[5]，并且导致城市间功能的重新定位和整合，“都市圈”的影响和辐射范围沿着轴向外扩散、蔓延，使不同节点城市形成网状连接。大经济圈的形成正是基于这样的原理，经历了点—线—面的发展轨迹。在空间上则表现为以增长极为中心沿“梯度”向多极方向动态变化。区域经济处于低水平的均质化阶段，整体经济发展水平落后；当区域经济进入极核化阶段，增长极具备较强的集聚力量，此时要素向极核集中，极核的产业结构升级加速，服务业成为经济增长的引擎；当区域经济进入点轴化和一体化阶段，服务业不仅仅局限于在极核发展，空间组织架构的形成与完善为服务业的区域性空间分布展开提供了强大的依托。从长三角的发展历史以及今后的发展趋势判断，长三角应该经历了中心城市—多中心的城市群—以大城市为中心的“都市圈”—广域集聚中心这样的一个形成过程。长三角的多中心城市群的发展使原本孤立、分散的块状经济向以城市为节点的新型经济网络体系发展，而“都市圈”的形成能充分发挥大、中、小城市合理的梯度分工，克服单一中心城市扩散效应随距离衰减的局限性和过度膨胀引起的不经济性。“都市圈”中作为金融、信息、技术以及人力资本枢纽的超级城市主要发展生产性服务业为主的技术密集型和资本密集型产业，重点放在信息交流、管理创新、产品技术研发、市场营销等价值链高端环节，同时参与国际化分工；大中城市作为“都市圈”内的次增长极，主要起传递和扩散的作用，承接来自超级城市的制造业和服务业的转移；底层的乡镇作为城市发展的腹地，主要参与国内分工，是零配件、小商品、农产品的加工基地。

城镇化是资源从农业部门转移到工业部门的过程。与之相关的模型有两部门模型和新经济地理模型，它们都考察了不同部门的转换，但是不包括城市和经济增长。两部门模型（two sector model）追溯可到刘易斯（Lewis，1954）考察部门之间的转换，是一个静态模型，主要关注城市的偏向性问题或者政府政策对城乡分割的影响。两部门模型有一个外生给定的“先进的”城市部门和一个“落后的”农村部门（Rannis和Fei，1961；Harris和Todaro，1970）。在模型当中，城市部门的劳动边际产品超过农村部门。劳动力流动由于无效的（外生给定的）劳动分配制度，如工人获得报酬是根据平均产品而非边际产品或者人为地限制城市部门对劳动力的吸纳，如制定部门最低工资。后来凯利和威廉逊（Kelley和Williamson，1984）以及贝克尔（Becker，1992）提出的相对复杂的两部门模型都是动态的一般均衡模型（CGE），包括储蓄行为、资本积累、人口增长。在城市和乡村地区有大量的经济部门，部门内和跨区域的劳动力市场都很明确。模型分析了政策工具的广泛影响，包括部分特殊贸易或者关于住宅、产业、服务等的资本市场政策。然而起点是外生给定的城乡生产率差距，并且开始取决于人口迁移成本和外生技术可获得性。城镇化过程是外生力量的结果，即技术进步或者贸易变革偏向城市。但是两部门模型用来解释城镇化过程仍有缺陷：首先，两部门的发展起点如何在模型中定义；其次，没有集聚力量使产业在城市部门集中；最后，尽管提到两个部门但是没有涉及空间和区域方面的问题。“中心—外围”模型（coreperiphery model，Krugman，1991）企图弥补这方面的缺陷，主要解决在一个双区域的国家内，在什么情况下工业化或者城镇化分散在不同区域，什么情况下集中在一个区域。克鲁格曼详细介绍了规模经济，它促进了区域的内生集中。有两个区域，不考虑起点，只假定一个区域的起点比另一个区域高，工业化同时发生在两个区域或者只发生在一个区域，在某种前提下一个区域落后或者不落后（收入水平低）但至少人口下降，模型中以交通成本来表示空间概念。“中心—外围”模型主要考察发展问题：中心地区（沿海地区）或者外围地区（内陆地区）的发展。但是“中心—外围”模型在城镇化方面的应用受到了限制，因为在其很多版本的模型当中，农业部门的人口是固定的，其只是单维度地考虑问题，如当区域之间的交通成本下降时，“中心—外围”结构将如何发展，而不考虑技术进步的存在。此外，“中心—外围”模型没有考虑到政策的影响，如工资补贴的影响、城乡贸易和资本市场的不完整性等。虽然其最大的贡献是引入了交通成本，但是却忽略了整个城市体系的作用。城市模型应该主要关注城市的形成过程，即城市部门是由许多城市构成，数量和规模都是内生的，政策要着眼于国内市场的不完整性、城市管理者和开发商的作用、城市内部的竞争，以及财政和税收的重要作用。

布莱克和亨德森（Black和Henderson，1999）提出了城市体系的内生增长模型，直接探讨城镇化与经济增长之间的关系。分析包括两部分：第一部分回顾传统的静态模型，集中在城市的形成、城市规模和数量的确定以及城市内部的产业结构等；第二部分是关于经济增长。

城市经济的增长模型由两部分组成。第一部分是城市部分，它描述了生产和人口的空间组织。在经济体当中，有一个国家的城市土地市场的形成过程，涉及土地、发展商或任何自治的地方政府。笔者假定经济中只有两种类型的城市，每一个城市执行不同的功能，城市之间存在不同规模的平衡、不同的人力资本水平和工人收入水平。每一种类型都包含许多城市，虽然对两种类型城市提供有限的分布规模，但已经足以确立起基本原则。在经济体中，属于类型1的城市生产基准价格商品和一个中间投入品，这些中间投入品被类型2城市当中的企业购买。类型2城市中的企业专业化生产消费品，相对于基准价格定价为P。这些城市绝对地专业化于贸易类商品的生产，城市之间的贸易无交易费用，回避了更多元化的特大城市在经济中的作用。例如，格莱泽（Glaeser等，1995）提出多样化有助于增长，亨德森（J．V．Henderson）等使用迪克西特—斯蒂格利茨模型（Dixit和Stiglitz，1977）作为基于城市里非贸易中间投入品部门多样化的城市规模经济的基础。不过，即使本地多样化是重要的，单个城市仍然需要有突出的专业化生产来满足城市之间种类更广泛的商品贸易。纽约的工业结构尽管存在巨大的多样化，仍然相对集中在金融、出版、时尚等行业，因此要建立起关于增长的基本准则。

第二部分城市增长模型的组成涉及家庭移民和人力资本的投资决定。在一个简单的世代重叠的模型当中说明人口的分布和各城市的人力资本分配。在家庭集团中，每一个家庭开始的时候人均人力资本是相同的，每一个家庭都以同样的增长速度g增长，每一个家庭未来的折扣率是ρ，如果ρ＞g，就能确保良好的解决方案。任何时刻，都要选择家庭总收入的一部分用于分配给每个成员消费，假定为c，表示分配多少用于增加家庭的人力资本存量。家庭成员必须分散在不同类型的城市中，并决定在各类型城市中居住的家庭成员的人均人力资本的投资。对于现有的家庭成员，当前所拥有的人力资本是不可转让的，只能期待新生儿。

对于整个家庭来说，每个人消费C产生的一般形式的最优效用函数为：

限制条件：

在方程（5－15）中，假定家庭初始规模为1，家庭在时间t的规模是egt，H是家庭的人力资本存量，z是家庭成员在类型1城市当中所占比重，1－z是家庭成员在类型2城市中所占比重，I1和I2分别代表了居住在类型1城市和类型2城市的工人的人均纯收入。相应地，h1和h2分别代表了他们各自的人力资本水平。接着建立I1和I2的表达式，要么被代入到约束条件或者看作额外的限制条件。

限制条件（a）的方程表达了家庭的人力资本增长值（P）在所有家庭收入zegtI1＋（1－z）egtI2和家庭消费Pcegt中是不同的。在限制条件（a）当中人力资本的形成是通过对类型2城市当中所生产商品的消费转换而来并且按照价格P出售。限制条件（b）表明整个家庭人力资本是位于类型1城市成员zegt和类型2城市的成员（1－z）egt单个人力资本（h1和h2）的总和。关于限制人力资本的转换有两个重要的假设。首先，限制条件（c）中表示家庭既不能出借也不能消费他们的人力资本，消费品到人力资本的转换是不可逆的。其次，对（c）的限制表明一旦建立起来，人力资本只能作为对同一类型城市的新生儿的捐赠是可转让的。限制条件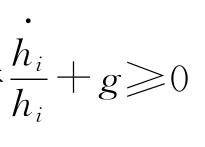表明在某种城市类型中的每一个成员的人力资本最大化的百分比就是他们后代的增长率，此外，还有其他限制，如人力资本对于任何产业或者城市都是特殊的，在跨城市之间的移民是部分或者全部不可转移的。

假定家庭成员在不同类型的城市收入不同，分别是I1和I2，为了维持人均消费的平等，一般情况下跨城市之间都会有一个家庭内部的转移成本C。对于公式的刚性约束可以做如下放宽：首先，不考虑父系社会特殊的家庭内部收入转移，考虑处在低人力资本城市的个体对处在高人力资本社会的家庭成员投资并且获得相应的补偿；其次，整个家庭可以分裂成若干小单位，只要每个小单位开始状态都有同样的人力资本存量H／egt；最后，如果存在人力资本市场，每一个家庭或者家庭单位都可以完全居住在一种类型的城市，向其他类型城市家庭的人力资本进行借入或者投资。为了优化方程（5－15），有必要决定真实收入I1和I2的表达式以及本地化知识或者人力资本溢出的细节。为此，笔者先研究城市的生产、城市的规模（会反过来影响人力资本投资的回报），然后研究方程（5－15）的家庭投资和移民问题。这些将决定整体人力资本水平的提高、城市的形成和增长以及城市规模的分布。

在上述的两种类型的城市中，每种类型的城市专业化于生产特定类型的商品。类型1城市的结构如下：城市中的每一个企业都只有一个工人组成。每一个时期工人决定生产多少或者对个人人力资本的积累投资多少。假设只有一个工人的企业，方便理解人力资本的溢出只能是跨企业的而不会在企业内部。在类型1城市的企业i产出为：

在方程（5－16a）中，n1是这个城市当中产业1的就业人数；h1是这个城市所有工人人力资本的平均水平；h1i是企业i工人的人力资本；δ1代表本地消费总量产生的规模经济，是n1的比例；企业i相对整个城市人力资本平均水平的产出弹性是ψ1，它代表了人力资本在本地的溢出效应。笔者使用本地化人力资本的平均水平而不是人力资本总量，因为规模经济是以nδ11的形式获得，hψ11看作nδ11知识溢出的丰富程度。方程（5－16b）说明了在类型1城市中工人i的私人收入W1i仅仅是这个工人的产出。

假定所有的工人都是相同的，存在一个对称均衡，在类型1城市中h1i＝ h1，整个城市的产出是n1X1i或者1。技术的特殊性在于人力资本溢出和规模外部性是本地化的。此外，规模外部性只针对本产业，本地区其他产业很难从X1产业中获得收益。集聚的人口进入城市要承担交通方面的成本，正如亨德森（Henderson，1974）所说的那样开发者将形成专业化城市。因为对于同样的人口和运输成本，拥有单个较大规模产业的专业化城市的人均产出比多样化城市中每个独立产业在较小规模上运行的人均产出要大得多。

1）上下班交通

所有的生产行为在城市中都发生在一个点上，也就是CBD。围绕CBD的是一圈住宅，那里每个居民生活在一定范围空间以每单位距离的固定成本τ往返于CBD。虽然基础建设投资、拥挤、污染等问题对于分析城市增长至关重要，但并不放在本模型中讨论。为了简化而又不失一般性，使用最简单的城市内部空间结构版本，在这个版本中土地市场的均衡通过租金斜率体现，从CBD到城市边缘呈线形递减，在城市边缘的租金为零。随着城市人口增加，城市规模扩大，平均的往返距离和租金斜率都在增加。也就是说，整个城市的往返交通费用和租金是根据城市人口确定的。住宅市场的均衡要求所有的居民居住在相同大小的场地并支付相同的租金R（u）加上运输成本τu，u是到CBD的距离，任何消费者都有相同的剩余用来投资或者购买其他商品。在半径为u的城市边缘的租金加交通成本是τu1，因为R（u1）＝0，其他地方是R（u）＋τu。让城市边缘和其他地方的租金加交通成本之和相等，得到租金率R（u）＝τ（u1－u）。由此可以计算这个城市的所有租金为或者是，总的交通成本是。给定城市的人口n和一个人居住空间的大小，n或者u1＝π－1／2n 1／2，替换得到方程（5－17）和（5－ 18）。?

所有交通成本为：

所有土地租金为：

其中。

方程（5－17）是重要的成本，其平均交通成本随着城市规模的增加而增加（弹性是1／2），就会形成压力限制城市规模的扩大。方程（5－18）构成了城市开发者的总的租金收入。

2）城市开发者

类型1城市都是由开发商控制，他们获取城市土地租金，吸引企业落户于这个城市，具体指定城市的人口（尽管人口在均衡条件下是自由移动的）。在全国范围内有许多潜在的相同的地点可以形成城市，但是每个开发商只选择控制一个地点，这就是传统规划（Hamilton，1975；Scotchmer，1986）。但是这个结论同样可以从其他方式获得。在静态条件下，亨德森和贝克尔（Henderson和Becker，2000）认为结论仅仅是证明联合均衡，同样发生在自组织模型当中，即每一个存在的城市是由一个独立的当地政府管理。在增长背景下，他们认为一个均衡的形成是开发商开始建立新城市并使利润最大化，而已经存在的城市转交给居民或者由独立的地方政府管理。在一个有代表性的城市，把开发商的最优化问题简化为一系列时间的利润最大化问题（Deo 和Duranton，1995），这个假设来源于一个如下简单事实：在模型中只有私人的人力资本，开发商不能对居民人力资本的积累进行投资。接着，会考虑制度的规范，即开发商可能会对人力资本进行投资使知识溢出内部化。一个开发商的瞬间利润是方程（5－18）的土地租金减去每个企业的迁移支付T1。开发商面对一个自由移民的条件下每个工人的净收入（扣除租金和交通成本）等于在其他类型1城市的劳动力市场上可获得的真实收入I1，开发商决定城市的类型和规定城市人口nl，迁移支付是T1，为了最大化当前利润。

限制条件：

从方程（5－15a）当中，假定在城市中存在对称性，将限制条件中T1的表达式带入到方程（5－19），令∏1＝0（开发商和城市在国家土地市场上自由进入）得到的结果是：

方程（5－20）的结果是所有对企业的迁移支付Tlnl等于城市全部的土地租金，当企业进入一个城市以后，由于提高了规模收益缩小了私人边际产品（方程5－16）和社会边际产品之间的差距（差距是δ1W1）。开发商或者政府有动力资助进入的企业，使本地规模的外部性收益在区域内部化。方程（5－21）的结论表明，均衡的城市大小是关于规模和其他参数的函数，同样也是人均人力资本的函数。二阶条件和方程（5－21）揭示了参数限制，在经济体当中有必要存在大量的类型1城市。方程（5－21）还说明了当规模弹性δ1增加到往返交通成本弹性1／2（根据方程5－17）时，城市规模也随着扩大。当时，所有X生产只发生在一个城市，因为城市规模扩大所带来的边1际规模收益总是超过边际成本。最后，假定方程（5－21）满足方程（5－19）的限制条件，城市的规模将是“自我加强型”，家庭也不能把人口从其他城市转移过来获得收益。

根据城市规模和人力资本的关系，2ε1定义了城市规模相对于人均人力资本的弹性，并且随着θ1和ψ1的增加而增加。ε1分解为私人收益部分φ1，外部性收益部分，规范的均衡解需要φ1＜1。当ε1作为规模经济的水平增加的时候，δ1也增加到交通成本弹性1／2。规模报酬放大了人力资本的回报，在方程（5－22）中，ε1是一个城市净收入相对于平均人力资本水平的弹性。当人力资本积累的时候，不仅收入增加，城市规模也在增加。为了解出收入W1和真实净收入I1，将方程（5－20）和（5－21）代入到方程（5－18）和方程（5－16a），城市产出是X1，得到：

3）类型2城市

类型2城市专业化生产消费品，在国内竞争市场上以价格P销售，拥有单个工人的企业产出为：

外部规模nδ22、人力资本hψ22和方程（5－16a）的X1i相对应，h2j是工人j的人力资本，X1j是第j个企业使用类型1城市所生产的中间投入品，一个企业的利润就是PX2j－X1j，选择X1j并代入PX2j－X1j，求出企业利润的最大化得到工人的剩余利益：

如同类型1城市，类型2城市的开发商决定城市类型和选择T2和n2确保，限制条件是。W2在方程（5－24）中已经给出，如果在城市内部对称条件下h2j＝h2，从类型1城市推出类型2城市的交通成本和租金，会发现交通成本和租金是根据X1这个计价商品来支付的。笔者按照前面的方法解决问题，令∏2＝0，得到的结论是T2 ＝1／2bn12／2，代入后对应方程（5－21）和（5－22），笔者可以定义均衡状态的城市规模方程（5－25）和实际收入方程（5－26）。

假定方程（5－15）家庭动态优化：(www.daowen.com)

如果忽略限制条件（c），则可以构造一个家庭的哈密尔顿（Hamiltonian）函数：

方程（5－27）不完整因为需要把每个家庭I1和I2的限制条件加进去，如家庭i所预想的，类型1城市的工人基于方程（5－19）和（5－16a），I1i＝W1i＋ ，而T1、h1和n1被认为是固定的。从而aI1i／ ah1i＝θ1W1i／h1i，如果假定对称（即h1i＝h1）且使用方程（5－21）和（5－22），那么a I1i／ah1i＝θ1／（1－2δ1）I1h1－1＝φ1I1h1－1，同样类型2城市的aI2i／ah2i＝θ2／（α－2δ2）I2h2－1＝φ2I2h2－1，对方程（5－27）求导并考虑到对称性且代入上述公式得到：

横截条件需要

在方程（5－28c）和（5－28d）中，家庭在不同类型城市之间进行人力资本配置来平衡私人的投资回报。当把两者结合起来得到I1／I2＝（φ2／φ1）h1／h2，然后又和从方程（5－28b）和（5－28c）当中解出的λ2／λ1结合起来，得到：

为了解出不同家庭成员在各类型城市中的比重需要解出z，并进一步考察国内市场上的均衡。

国内市场的均衡需要城市之间的贸易平衡，也就是类型1城市的供给等于类型2城市的需求。全国对X1的供给是m1X1，m1是类型1城市的个数，m2是类型2城市引进X1作为中间投入品x1的数量，使用X1会在两种类型的城市产生交通成本。贸易平衡需要m1X1＝m2n2x1＋m1（bn31／2）＋m2 （bn32／2）。采用对称性，每一个家庭分配相同比例的工人去不同类型的城市，在每一时刻，z＝m1n1／N且1－z＝m2n2／N，N是全国总人口。当令需求等于供给时，m1（X1－bn31／2）＝m2n2［（x1／n2）＋bn12／2］。从方程（5－19）、（5－15）和（5－20）得出n1I1＝X1－bn31／2，从方程（5－24）和（5－25）得出（x1／n2）＋bn12

／2＝I2（1－α＋2δ2）／（α－2δ2）。把这些关系联系起来得到m1n1I1＝m2n2I2（1－α＋2δ2）／（α－2δ2），将方程与方程（5－29b）以及z＝m1n1／N和1－z＝m2n2／N结合起来代入得到z，如方程（5－30）。

任何家庭中去类型1城市的工人的比重z相对于h（h1或者h2）都是不变的，相对于时间也是一个常数，就算所有工人被指派到一个城市也不会改变它的类型。并且可以解出类型1和类型2城市的数量ml和m2，在某一时刻作为全国人口N的函数，将方程（5－30）和z＝m1n1／N结合起来得到：

解出反映人口迁移计划的z，同时也能够解出人力资本的使用h1或h2，h作为人均家庭资本储备的函数，假定h＝He－gt，根据方程（5－15）的限制条件（b）中得到h＝zh1＋（1－z）h2代入方程（5－29）和（5－31）得到

方程（5－30）直接告诉我们家庭成员的相对分布不会因城市类型而变化，根据方程（5－29）和后面的（5－35），对时间差分。人力资本以同样的速率在两种类型城市平行的增长。唯一的资本传递发生在工人和他们的孩子之间，平衡条件下，针对专门的技术（X1或者X2）人们相互之间无法传递人力资本。最后结合方程（5－29）和z ＝m1n1／N且1－z＝m2n2／N代入后得到：

在方程（5－33）中，假如ε1＞ε2，当h增加时，消费品的相对价格也增加。如果生产基准计价物类型城市的收入相对人力资本的弹性超过在生产消费品类型的城市，则P增加，因而消费品变得更贵重。结果总结为以下几部分：首先，资源在各城市之间的分布均衡包括以下特征：①人力资本和人均收入的比率，h1／h2和I1／I2是不随时间变化的，这意味着持续被测量的真实收入不平等，即I1＞（或＜）I2和hl＞（或＜）h2当φ1＞（或＜）φ2时，φi表示在类型i城市当中人力资本投资的私人回报。②人口在跨城市之间的相对分布也不随时间变化的。③当ε1＞（或＜）ε2时，εi是类型i城市人力资本投资的社会回报，消费品X2的价格P随着人力资本的积累提高或者降低。不仅考虑真实收入还要考虑收入的不平等，给定人力资本水平I1和I2，随城市类型不同而变化，但是名义收入W1和W2的差异化是给定的，此外，不同城市的生活成本也存在差异，所以W1／W2＝（α－2δ2）（1－2δ1）－1α－1（I1／I2）。

尽管每一种类型城市的人均人力资本水平随时间变化，在每一种类型城

市的人力资本都以相同速度增长，，在城市规模方程（5－ 21）和（5－25）结合方程（5－33）中的P，得到

小圆点代表时间导数，单个城市规模增加是人力资本积累增加速度的2ε1倍。ε1是类型1城市的人力资本水平的收入弹性。如果经济经历稳态增长，ε1就会接近1，城市规模增长速度就会接近人力资本积累速度的2倍。尽管外部性提高了城市新增人口的边际收益，人力资本的积累提高了人均劳动生产率，使城市规模的增长超过人力资本的积累。但城市数量的增加是怎么样的情况呢？从方程（5－31）给出了m1和，其中全国人口增长速度由方程（5－34）给出。然后

如果由人力资本积累所引发的单个城市规模的扩大不是以容纳快速增长的总人口，城市数量就会增加，单个城市规模的增长速度与人力资本的积累速度是成比例的。假定各类型城市的相对规模和数量不随时间变化，跨类型的城市增长是平行的，相对规模分布是保持固定的。

根据奎格利（Quigley，2008）的结论，交通成本和内部规模经济不是城市存在的唯一的经济学解释，否则城镇化对经济增长的作用就会非常有限。在现代经济当中，城市发展的意义主要是外部性效应（external effects）和知识溢出（knowledge spillover）。这些因素都与工业化水平提高、技术进步和经济发展密不可分。其中，外部性效应有很多定义和分类，最常用的定义来自于专业化分工，主要产生于大量相邻的经济个体之间的相互影响，包括教育、知识传递、模仿等。下面从四个方面论述城市集聚效应的产生。

专业化的益处是在密集的城市中出现了较多的生产型企业，可以支持更多专业生产中间产品的企业。专业化可以提供更多减少商品生产成本的机会。例如，当部分中间产品可常规生产时或最终产品可机械化或自动化生产时，生产效率就会大幅度提高。同时，专业化生产的收益也会延伸到生产型服务业。例如，专门的法律服务，专业从事会计、版权、担保交易等可提供更有效率服务的公司。不管是生产商品还是服务的中间商，专业化生产都增加了降低成本的机会。专业化生产的潜在收益是进一步提高在企业之间共享投入的机会，这些在规模更大、更密集的城市地区更容易实现。例如，修理、印刷、广告和通讯等专业服务只要实体经营场所的密度足够高，就可提供给更广泛的商品生产者。如果满足最终需求的生产企业本身围绕着相同行业或产品在空间上更集中，专业化生产的外部收益就会出现，从而产生了本土化经济。但是，如果满足最终需求的企业生产不同的商品却在空间上密集，外部性收益也可能产生，从而导致城镇化经济。在这两种情况下，允许提供更多的中间产品和服务的企业进行专业化生产，进而导致成本降低。

因为更大的城市规模有利于更好地在工人技能和工作要求之间或者在生产中间产品和最终产品的需求之间匹配，所以可能导致交易成本的外部性和生产的互补性。例如，劳动力市场有效降低了拥有不同技能的劳动者寻找更好工作机会的搜寻成本，也降低了不同需求的雇主寻找各自满意雇员的搜索成本。在物质资本和人力资本之间的互补性生产，意味着城市劳动力蓄水池里有比较大的人力资本存量，预计雇用这些工人的企业将更多地投资于有形资本。在搜索成本昂贵和城市劳动力市场匹配不完善的情况下，一些低技能的工人将最终处理更多的物质资本，他们会变得更有生产效率并且赚取更高的收入。工人的人力资本回报和雇主的有形资本回报都会随着城市人力资本存量的增加而增加，即使在每个工地都是按照规模报酬不变的方式进行生产。

运用在劳动力市场匹配方面的互补性概念区别于在人口稠密的城市地区拥有相似教育程度和技能的劳动者集群所产生的外部性。生产力的溢出即受过教育的或有技能的工人会提高其他工人的生产率，不管城市产业结构是多元化还是专业化，可能会出现生产密集的空间环境。在这样的集群环境中便于企业之间的技术传播、复制和创新，企业之间的专利家谱都能作为例子说明地方化生产的外部性，这种生产外部性因为城市密度和集中在一起的熟练工人彼此接近而得到加强。这些经济体可能使产业在空间上集中（本地化经济）或更高密度的不同行业集中（城镇化经济）。

最后，当大量的经济主体互相接近时可能会节省可观的成本。例如，从某种程度上来说，在城市劳动力市场的需求波动和企业之间的相互作用是不完全相关的，既然有些企业打算雇用工人而其他公司将缩减雇员，那么就业是可以保持稳定的。在一定程度上，对产品需求的波动在买家之间不相关，企业希望承担较少的库存，因为一些消费者需要购买而另一些则不需要。大量的不完全相关的经济行为主体在相互接近状态下所作出的决定可以提供一种自然形式的保险。来自大数定理的基本观点很简单，它可以根据较大样本的空间对分布曲线在每一个时刻得到较好的估计，这方便所有经济行为主体根据最佳信息作出判断。这对市场买卖双方进行投入品采购、中间产品储存、产品销售等情况都是适用的。

根据增长极理论，区域经济发展过程中先以回流作用为主导，随着集聚不经济的增加，扩散作用开始取代回流作用成为主导机制。本章之所以选择长三角作为研究对象是因为其特殊的发展阶段。长三角的经济增长多年来明显高于全国平均水平，内部空间结构开始由多中心向一体化趋势迈进，这正是扩散机制开始发挥主导作用的现实依据（在经济落后地区扩散机制可能并不显著）。目前，长三角的城镇体系主要包括特大城市、大城市、中等城市、小城市、小城镇组成的五个等级层次，等级层次愈高，城市越少，呈现明显的金字塔格局。城镇化水平也在不同层次间存在差异，规模越大、层次越高的城市，城镇化水平也越高。由于中心城市在集聚过程中的能量溢出产生辐射效应，所以中心城市辐射能力的强度同城市本身所处的等级层次有关，等级层次越高的城市，集聚效应越强，释放的能量也越大，辐射范围也越广，而且传递的方向是由高到低，呈梯度扩散的。

目前，国内外对集聚、扩散效用的定性研究成果比较多，定量研究却非常少。吴玉鸣、徐建华（2004）与吴玉鸣（2006a；2006b）使用地域范围较大的省级数据对中国区域经济增长的集聚现象作过研究，但是没有揭示城市增长极对同级或者下级市、县经济增长的扩散作用。柯善咨（2009）根据增长极和非均衡增长理论构建了扩散和回流的实证模型，使用空间计量经济学联立方程对中部地区6省579个市、县在2000—2005年间的非农产业经济增长和溢出效应进行分析，并且将扩散的范围纳入其实证研究中。结果表明，中国中部地区城市增长极的扩散和回流效应主要存在于50千米—100千米范围内。在此范围内，地级及以上城市间GDP增长相互促进作用，对县级市和未设市的县镇有显著的扩散作用；县级市GDP增长对邻区县级市GDP增长有促进作用，但是对邻区未设市县镇的GDP增长有显著的回流效应。

为了说明城镇化集聚—扩散机制的影响，本章研究对象是长三角两省一市共计132个市、县。除了上海这个直辖市以外，还包括浙江省的杭州市（富阳市、临安市、建德市、桐庐县、淳安县）、宁波市（余姚市、慈溪市、奉化市、象山县、宁海县）、温州市（瑞安市、乐清市、洞头县、永嘉县、平阳县、苍南县、文成县、泰顺县）、嘉兴市（平湖市、海宁市、桐乡市、嘉善县、海盐县）、湖州市（德清县、长兴县、安吉县）、绍兴市（诸暨市、上虞市、嵊州市、绍兴县）、金华市（兰溪市、东阳市、义乌市、永康市、武义县、浦江县、磐安县）、衢州市（江山市、常山县、开化县、龙游县）、舟山市（岱山县、嵊泗县）、台州市（温岭市、临海市、玉环县、三门县、天台县、仙居县）、丽水市（龙泉市、青田县、云和县、庆元县、缙云县、遂昌县、松阳县、景宁自治县）以及江苏省的南京市（溧水县、高淳县）、无锡市（江阴市、宜兴市）、徐州市（丰县、沛县、睢宁县、新沂市、邳州市）、常州市（溧阳市、金坛市）、苏州市（常熟市、张家港市、昆山市、吴江市、太仓市）、南通市（海安县、如东县、启东市、如皋市、海门市）、连云港市（赣榆县、东海县、灌云县、灌南县）、淮安市（涟水县、洪泽县、盱眙县、金湖县）、盐城市（响水县、滨海县、阜宁县、射阳县、建湖县、东台市、大丰市）、扬州市（宝应县、仪征市、高邮市）、镇江市（丹阳市、扬中市、句容市）、泰州市（兴化市、靖江市、泰兴市、姜堰市）、宿迁市（沭阳县、泗阳县、泗洪县）。

空间计量经济学模型有多种。（Anselin等，2004）笔者使用的空间计量经济模型主要是纳入了空间效应（空间相关和空间差异）的空间常系数回归模型，包括空间滞后模型（spatial lag model，SLM）与空间误差模型（spatial error model，SEM）两种。

1）空间滞后模型（SLM）

该模型主要是探讨各变量在某一地区是否有扩散现象（溢出效应）。其模型表达式为：

方程（5－36）中，y为因变量；X为n×k的外生解释变量矩阵；ρ为空间回归关系数；W为n×n阶的空间权值矩阵，一般用邻接矩阵（contiguity matrix）；Wy为空间滞后因变量；ε为随机误差项向量。

2）空间误差模型（SEM）

该模型的数学表达式为：

方程（5－37）中，ε为随机误差项向量，λ为n×1的截面因变量向量的空间误差系数，μ为正态分布的随机误差向量。

根据柯布－道格拉斯（Cobb－Douglas）型生产函数建立如下基本方程：

其中，i代表某个城市，t代表时间，Y为国内生产总值，L为劳动，K为资本，A为技术水平。

把方程（5－38）滞后一期，对两边求对数得出关于增长率的模型，即

其中，A是全要素生产率，看作除资本和劳动以外的所有影响经济增长的因素。影响经济增长的因素很多，如初始经济发展水平、区位、投资、产业、人力资本、对外贸易、市场规模、政府政策、环境和文化等。同时，相邻地区在产出和就业上存在互补和竞争的关系，一个地区的产出受其相邻城市的影响。此外，影响具有累积性，即前期的因素会影响后期的经济增长，即所谓的动态的外部性。

其中，∑σixi是所有影响全要素生产率A变化的因素集合，WY表示相邻地区的产出，Wx表示所有来自相邻地区的外部性。将方程（5－40）代入到方程（5－39）整理得到：

或者

其中，εi是随机误差项，假设其服从独立正态分布εi～N（0，σ2），且E（εiεj）＝0。

因为在浙江省农业产业比重（产值和就业）非常低[7]，本章忽略农业与非农业增长之间的差别，直接用人均GDP作为解释变量Y。K表示人均固定资产投资，L表示就业人口。根据柯善咨（2009）、吴玉鸣和徐建华（2004）的研究以及数据的可得性，A的变量包括人口密度（Density）、医疗设施（Hospital bed）、通讯条件（Telephone）、市内交通条件（Road）、人力资本（Human）、外商直接投资（FDI）以及政府财政支出（Expenditure）。变量定义与统计描述见表5－1。

本章基础年份的数据主要来自于2001和2012年版的《中国城市统计年鉴》《浙江省统计年鉴》《上海市统计年鉴》和《江苏省统计年鉴》。

1）计量模型的判别流程

安瑟林（Anselin，1988）建议采用极大似然法估计空间滞后模型（SLM）和空间误差模型（SEM）的参数。判断地区间经济行为的空间相关性是否存在，一般通过Moran I检验、两个拉格朗日乘数（lagrange multiplier）形式LMERR、LMLAG和稳健的R－LMERR、R－LMLAG等来判断（吴玉鸣，2006a；2006b），如图5－1所示。

对于是采用一般的线性回归模型，还是采用SLM或SEM更加符合客观实际，可以依据安瑟林（Anselin，2004）提出的判别准则：如果在空间依赖性的检验中发现，LMLAG较之LMERR在统计上更加显著，且R－LMLAG显著而R－LMERR不显著，则可以断定适合的模型是空间滞后模型；相反，如果LMERR比LMLAG在统计上更加显著，且R－LMERR显著而R－LMLAG不显著，则可以断定空间误差模型是恰当的模型。除了拟合优度R2检验以外，常用的检验准则还有自然对数似然函数值（log likelihood，LogL）、似然比率（likelihood ratio，LR）、赤池信息准则（Akaike information criterion，AIC）和施瓦茨准则（Schwartz criterion，SC）。对数似然值越大，似然比率越小，AIC 和SC值越小，模型拟合效果就越好。这几个指标也用来比较OLS估计的经典线性回归模型和SLM、SEM，似然值的自然对数最大的模型哪个最好（吴玉鸣，2006a；2006b）。

2）空间权重矩阵的定义

在空间数据分析中要求把空间或者位置信息以数值的形式表式。空间权重矩阵的选取是空间数据分析中最关键也是最重要的部分。对于空间权重元素Wij定义的标准有很多，最常用的就是邻接标准和距离标准。邻接标准的规则是区域i和区域j在地理空间上有共同的边界定义为相邻。

其中，i＝1，2，…，n；j＝1，2，…，m。

距离标准是当区域i和区域j之间的距离在给定距离范围（如d）内时，权重元素值定为1，否则为0。

图5－1　空间计量模型的判断流程

（源自：Anselin L：《Exploring spatial data with GeoDaTM：a workbook》，University of Illinois，Urbana－Champaign2004年版。）

选择距离标准构建权重矩阵时，所选的距离不能小于“门槛距离”[8]。如果设定的距离小于此值，会出现“孤岛”。对于特定的情况，一些实验（和连接结构检查）需要设定比最小门槛大些的值。本章根据地图上长三角的各个地区，相对位置，按照高阶邻接标准创建空间权重矩阵。

随着城镇化发展，城市结构和城市体系的发育状况影响了行政区划的调整，县域经济的发展壮大使一些地区升级为县级市，还有一些地方撤市（县）设区，提升了中心城市的竞争力和辐射力。为了使2000年和2011年的统计数据具有一致性和可比性，本章将前后年份的行政区划统一起来，以2011年为标准将2000年的萧山区和余杭区并入杭州市，鄞县并入宁波市，衢县和柯城区并入衢州市，椒江、路桥、黄岩并入台州市，鹿城区、龙湾区、瓯海县并入温州市。江苏省的淮阴市、淮阴县并入淮安市，江宁县并入南京市，锡山市并入无锡市，宿豫县并入宿迁市，盐都县并入盐城市，吴县并入苏州市，武进并入常州市，邗江并入扬州市，丹徒并入镇江市，江都市并入为扬州市，通州市并入南通市，铜山县并入徐州市。

首先利用普通最小二乘（OLS）法和极大似然估计（ML）法对方程（5－28）和（5－29）进行估计，然后通过Moran指数、拉格朗日乘数来判断空间计量经济学模型的形式。结果见表5－2，OLS估计的拟合优度检验值R2为71．98%，SLM和SEM的R2分别为72．00%和74．03%。由于采用ML法来估计参数，基于残差平方和分解的拟合优度检验意义不大。Moran指数检验证实了长三角县、市之间的经济增长存在空间自相关性，如果忽视空间自相关性而直接采用经典线性回归模型的OLS估计将会出现偏差。由此可见，任何地区的产出都不是独立的，都受到其他地区溢出效应的影响。

由空间依赖性检验结果可知，LMERR和R－LMERR都通过了5%水平下的显著性检验，LMLAG、R－LMLAG均未能通过10%水平下的显著性检验。根据上述判别准则，可以断定空间误差模型（SEM）是恰当的模型。比较SLM和SEM模型的对数似然函数值LogL、LR、AIC和SC值，SLM和SEM的自然对数似然函数值LogL（－7．3754、－4．3409）都比OLS（－7．4239）估计的结果大，其中SEM的LogL值最大，但是SEM的AIC（28．6819）和SC （57．6603）都比SLM的（36．7507、68．6271）小，这进一步证明了采用空间计量模型比经典线性回归模型拟合效果好，并且相对而言，采用SEM模型更合适些。根据空间误差模型的意义，它同时包含了两种空间溢出效应：一方面通过内生的空间滞后变量受相邻地区经济增长的影响，另一方面也可以通过外生空间滞后变量受邻近地区影响经济增长因素的影响。当然，这种判断不十分严格，为了方便比较，笔者同时给出了OLS、SLM和SEM的估计结果（表5－2）。其中，资本对经济增长的贡献为正且显著，而劳动的贡献虽然不显著都为负，表明长三角经济增长主要是靠资本推动，资本投入水平是造成地区之间增长差异的主要因素，而劳动生产率水平偏低将成为制约经济进一步发展的瓶颈。在SEM模型中除了资本以外，体现社会保障水平的医疗条件、人力资本、通信网络、政府支持以及来自其他地区集聚和扩散的效应都是影响本地区经济增长的重要因素。此外，市内交通条件这个指标也对经济增长产生负效应，虽然未通过10%的显著性检验，但说明今后在交通基础设施建设方面有待进一步加强和完善。

本章主要研究集聚—扩散机制，它是经济活动运行的前提和基础。集聚—扩散机制在区域经济发展的不同阶段起的作用不同，在中心城镇化阶段发挥主导作用，在郊区城镇化或逆城镇化阶段，扩散力量占主导。新型城镇化既强调发展一批具有影响力、带动力和竞争力的大城市，强化大城市的产业支撑，充分激发大城市聚集和辐射能力，又要推进那些工业基础较好、交通便利、综合承载力较强的中小城市发展，强化其与大城市的经济联系；既要发展新型工业化又要改造传统农业，转变农业增长方式，加快农业现代化发展。本章的研究侧重于理论分析，主要介绍田渊（T．Tabuchi）和亨德森（J．V．Henderson）等人的理论模型，借此说明集聚—扩散机制的内涵以及城镇化与城市体系的发展。根据奎格利（Quigley，2008）的结论，在现代经济当中，城市发展的意义主要是外部性效应（external effects）和知识溢出（knowledge spillovers），这些因素都与工业化水平提高、技术进步和经济发展密不可分。其中，外部性效应有很多定义和分类，最常用的定义来自于专业化分工，主要产生于大量相邻的经济个体之间的相互影响，包括教育、知识传递、模仿等。最后，本章又利用空间计量模型对长三角两省一市共计132个市、县经济增长的影响因素和相邻地区关联性进行实证检验，结果说明，任何地区的产出都不是独立的，都受到其他地区溢出效应的影响。通过与经典线性回归模型的比较后发现，采用空间计量模型的拟合效果更好，再次证实了相邻地区之间集聚—扩散机制的存在。

[1]在许多文献中，对扩散的研究主要集中在知识溢出（knowledge spillover）。

[2]Polanyi（1958）把知识分为两类，即编码知识（codified knowledge）和默会知识（tacit knowledge），编码知识指的是正式的知识，或者是可以书面化的知识，默会知识则是指非得言传身教的知识。

[3]同一产业的企业集聚会产生地方化经济（马歇尔外部性），多样化产业集聚会产生城镇化经济（Jacobs外部性）。

[4]浙江省人民政府办公厅：《关于开展小城市培育试点的通知》，2010。

[5]“都市圈”（metropolitan area）是因城市间功能聚集、运作协同、点—圈—线式空间结构布局日趋突出所形成的城市区域。“都市圈”是城镇化进程中的高级阶段，是在城市群的基础上形成的。与城市群相比，“都市圈”内城市间不仅限于物理上的空间关系，还实现了功能上的整合。

[6]在亨德森（J．V．Henderson）的模型当中，假设城市都是专业化生产的，但在各种条件下这都是一个均衡结果。因为他将城市之间的运输成本设为零，所有的运输成本都内部化为城市范围内，如果假定规模收益来源于产业内部的地方化经济，任何专业化城市的优越性都将超过多样化城市。比如，一个混合型城市产业1和产业2分别有n1和n2个工人，把这个城市分成两个专业化城市，一个城市有n1个工人，另一个有n2个，规模经济来自于产业内部并没有降低，分别为nδ11和nδ22，但是小的专业化城市的人均交通成本比大的混合型城市要低，而实际收入要高。

[7]根据《浙江省统计年鉴》，2000年时浙江省第二、三产业产值比重占到89．8%，到2007年比重上升到95%以上。

[8]保证每一位置都至少有一个邻居的距离。