5.7　节点设计原理

整个结构是由构件和节点（connection）构成的。单个构件必须通过节点相连接，协同工作才能形成结构整体。即使每个构件都能满足安全使用的要求，如果节点设计处理不恰当，连接节点的破坏，也常会引起整个结构的破坏。可见，要使结构能够满足预定功能的要求，正确的节点设计与构件设计，两者具有同等的重要性。

由于连接节点受力状态较为复杂，不易精确地分析其工作状态。所以，在节点设计时应遵循下列基本原则:

1．连接节点应有明确的传力路线和可靠的构造保证

传力应均匀和分散，尽可能减少应力集中现象。在节点设计过程中，一方面要根据节点构造的实际受力状况，选择合理的结构计算简图；另一方面节点构造要与结构的计算简图相一致。避免因节点构造不恰当而改变结构或构件的受力状态，并尽可能地使节点计算简图接近于节点实际工作情况。

2．便于制作、运输和安装

节点构造设计是否恰当，对制作和安装影响很大。节点设计便于施工，则施工效率高，成本降低；反之，则成本高，且工程质量不易保证。所以应尽量简化节点构造。

3．经济合理

要对设计、制作和施工安装等方面综合考虑后，确定最合适的方案。在省工时与省材料之间选择最佳平衡。尽可能减少节点类型，连接节点做到定型化、标准化。

各类节点的具体构造不尽相同，也很难同时满足上述各项原则。总起来说，首先节点能够保证具有良好的承载能力，使结构或构件可以安全可靠的工作；其次则是使施工方便和经济合理。

5.7.1　次梁与主梁的连接节点

次梁与主梁的连接有铰接（hinged connection或simpleframingconnection）和刚接（fully restrainedconnection）两种。若次梁按简支梁或连续梁计算，但在连接节点处只传递次梁的竖向支座反力，其连接为铰接。若次梁按连续梁计算，连接节点除传递次梁的竖向支座反力外，还能同时传递次梁的端弯矩，其连接为刚接。

次梁与主梁的铰接形式按其连接相对位置的不同，可分为叠接和平接两种。

5.7.1.1　次梁与主梁铰接

1．叠接

叠接是把单跨次梁直接放在主梁上，如图5-21所示，并用焊缝或螺栓固定其相互间位置。当次梁支座反力较大时，应在主梁支承次梁的位置设置支承加劲肋，以避免主梁腹板承受过大的局部压力。主梁腹板横向加劲肋的间距要结合次梁的支承位置来确定。

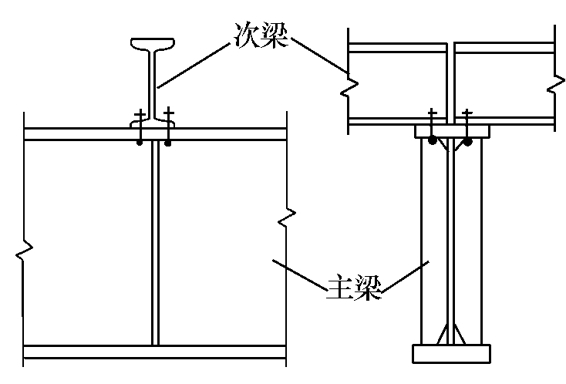
图5-21　次梁与主梁的叠接（1）

另一种叠接做法是次梁在主梁上连续通过，如图5-22所示。由于次梁本身是连续的，次梁支座弯矩可以直接传递。当次梁需要拼接时，拼接位置应选择在弯矩较小处。当次梁荷载较大或主梁上翼缘较宽时，可在主梁支承次梁处设置焊于主梁中心的垫板，以保证次梁支座反力以集中力的形式传给主梁，避免主梁受扭作用（图5-23）。这种连接的优点是构造简单，次梁安装方便；缺点是主次梁结构所占空间大，其使用常受到限制。

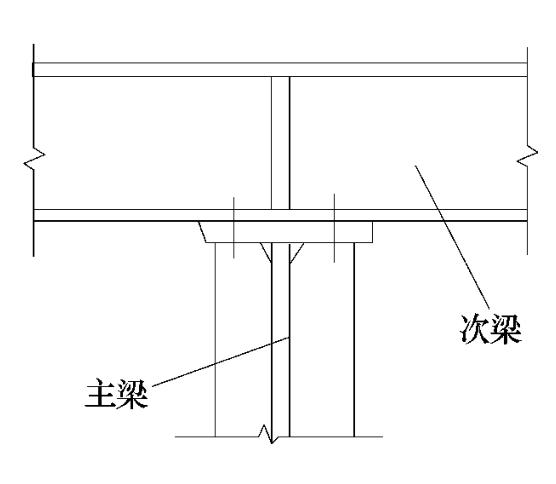
图5-22　次梁与主梁的叠接（2）

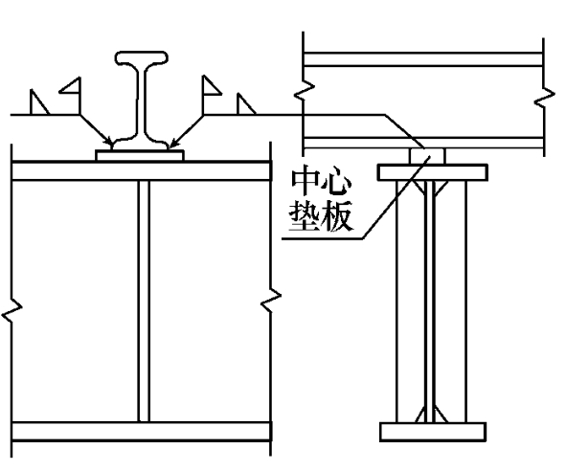
图5-23　主梁的中心垫板

2．平接

平接是将次梁连接在主梁的侧面（图5-24），可以直接连在主梁的加劲肋［图5-24（a）］、短角钢［图5-24（b）］和承托［图5-24（c）］上。次梁顶面根据需要可以与主梁顶面相平，或比主梁顶面稍低。平接可以降低结构高度，故在实际工程中应用较为广泛。

图5-24（a）、（b）中的连接构造，需将次梁的翼缘局部切除。考虑到连接处有一定的约束作用，并非理想铰接，通常将次梁支座反力值加大20％～30％进行连接计算。当次梁的支座反力较大，用螺栓连接不能满足要求时，可采用工地焊缝连接承受支座反力，此时螺栓仅起安装和临时固定位置的作用。

图5-24（c）适用于次梁支座反力较大的情况。支座反力全部由承托传递，支座反力引起的压力在承托上面按三角形分布，反力合力作用点位于承托顶板外边缘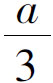处［图5-25（c）］。次梁端部的腹板应采取适当的固定措施防止支座处截面的扭转。

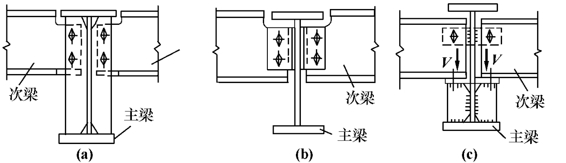
图5-24　次梁与主梁的平接

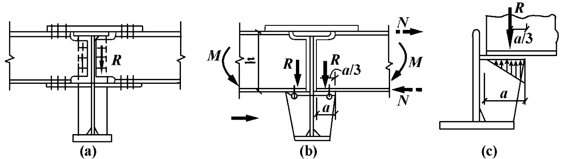
图5-25　次梁与主梁的平接

5.7.1.2　次梁与主梁刚接

次梁与主梁刚接时，由于连接节点除传递次梁的竖向支反力外，还要传递次梁的梁端弯矩，当主梁两侧的次梁梁端弯矩相差较大时，会使主梁受扭，对主梁不利。因此，只有当主梁两侧次梁的梁端弯矩差较小时，才采用这种连接方式。

次梁与主梁的刚接常采用平接形式。此时，次梁连接在主梁的侧面，并与主梁刚接，两相邻次梁成为支承于主梁侧面的连续梁（图5-25）。为此，两跨次梁之间必须保证能够传递其支座弯矩。图5-25（a）为采用高强度螺栓连接。图5-25（b）为次梁支承在主梁的承托上，采用焊接连接。由于次梁弯矩主要由其翼缘承受，所以在次梁翼缘上应设置连接盖板。次梁支座负弯矩M可以分解为上翼缘拉力和下翼缘压力的力偶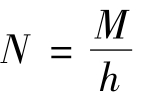（h为次梁高度）。计算时，次梁上、下翼缘与连接板的螺栓连接或焊接连接要满足承受N力的要求。次梁的竖向支座反力R则通过螺栓传给主梁腹板加劲肋［图5-25（a）］，或直接通过次梁梁端承压传给主梁的承托［图5-25（b）］。次梁的竖向支座反力只在承托顶板上的作用位置可视为距承托外边缘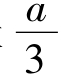处，承托顶板上的压力为三角形分布［图5-25（c）］。

5.7.2　梁与柱的连接节点

梁与柱的连接一般可分为三类:其一，铰接连接，这种连接柱身只承受梁端的竖向剪力，梁与柱轴线间的夹角可以自由改变，节点的转动不受约束；其二，刚性连接，这种连接柱身在承受梁端竖向剪力的同时，还将承受梁端传递的弯矩，梁与柱轴线间的夹角在节点转动时保持不变；其三，半刚性连接（padially restrained connetion），介于铰接连接和刚性连接之间，这种连接除承受端传来的竖向剪力外，还可以承受一定数量的弯矩，梁与柱轴线间的夹角在节点转动时将有所改变，但又受到一定程度的约束。在实际工程中，上述理想的刚性连接是很少存在的。通常，按梁端弯矩与梁柱曲线相对转角之间的关系，确定梁与柱连接节点的类型。当梁与柱的连接节点只能传递理想刚性连接弯矩的20％以下时，即可认为是铰接连接。当梁与柱的连接节点能够承受理想刚性连接弯矩的90％以上时，即可认为是刚性连接。半刚性连接的弯矩—转角关系较为复杂，它随连接形式、构造细节的不同而异。进行结构设计时，必须通过试验或其他方法提供较为准确的节点弯矩—转角关系。设计部门很难办到，因此目前较少采用半刚性连接节点。

5.7.2.1　梁与柱的铰接连接

1．梁支承于柱顶的铰接连接

图5-26为梁支承在柱顶的铰接构造。梁的支座反力通过柱顶板传给柱身，顶板与柱身采用焊缝连接。每个梁端与柱采用螺栓连接，使其位置固定在柱顶板上。顶板厚度一般取16～20mm。

在图5-26（a）中，梁端加劲肋对准柱的翼缘板，使梁的支座反力通过梁端加劲肋直接传给柱的翼缘。这种连接形式构造简单，施工方便，适用于相邻梁的支座反力相等或差值较小的情况。当两相邻梁支座反力不等且相差较大时（例如左跨梁有活荷载，右跨梁无活荷载），柱将产生较大的偏心弯矩。设计时柱身除按轴心受压构件计算外，还应按压弯构件进行验算。两相邻梁在调整、安装就位后，用连接板和螺栓在靠近梁下翼缘处连接起来。

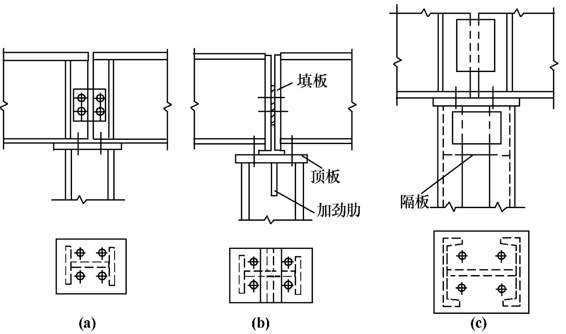
图5-26　梁支承于柱顶的铰接连接

在图5-26（b）中，梁端采用突缘支座，突缘板底部刨平（或铣平），与柱顶板直接顶紧，梁的支座反力通过突缘板作用在柱身的轴线附近。这种连接即使两相邻梁支座反力不相等时，对柱所产生的偏心弯矩也很小，柱仍接近轴心受压状态。梁的支座反力主要由柱的腹板来承受，所以柱腹板的厚度不能太薄。在柱顶板之下的柱腹板上应设置一对加劲肋以加强腹板。加劲肋与柱腹板的竖向焊缝连接要按同时传递剪力和弯矩计算，因此加劲肋要有足够的长度，以满足焊缝强度和应力均匀扩散的要求。加劲肋与顶板的水平焊缝连接应按传力需要计算。为了加强柱顶板的抗弯刚度，在柱顶板中心部位加焊一块垫板。为了便于制造和安装，两相邻梁之间预留10～20mm间隙。在靠近梁下翼缘处的梁支座突缘板间填以合适的填板，并用螺栓相连。

图5-26（c）为梁支承在格构式柱顶的铰接连接构造。为了保证格构式柱两单肢受力均匀，不论是缀条式还是缀板式柱，在柱顶处应设置端缀板，并在两个单肢的腹板内侧中央处设置竖向隔板，使格构式柱在柱头一段变为实腹式。这样，梁支承在格构式柱顶连接构造可与实腹式柱的同样处理。

2．梁支承于柱侧面的铰接连接

梁连接在柱的侧面上，在柱侧面设置承托，以支承梁的支座反力，其铰接构造如图5-27所示。

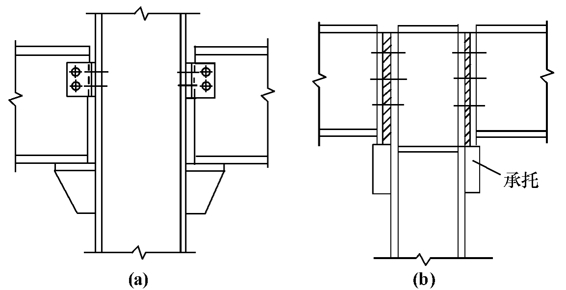
图5-27　梁支承于柱侧面的铰接连接

当梁的支座反力不大时，可采用如图5-27（a）所示的连接构造。梁端可不设支承加劲肋，直接放在柱的承托上，用普通螺栓固定其位置。梁端与柱侧面预留一定间隙，在梁腹板靠近上翼缘处设一短角钢和柱身相连，以防止梁端向平面外方向产生偏移。这种连接形式比较简单，施工方便。

当梁的支座反力较大时，可采用如图5-27（b）所示的连接构造。梁的支座反力由突缘板传给承托，承托一般用厚钢板制作，有时为了安装方便，也可采用加劲后的角钢。承托的厚度应比梁端突缘板的厚度大10～12mm，承托的宽度应比梁端突缘板的宽度大10mm。承托与柱侧面用焊缝相连。承托的顶面应刨平，和梁端突缘板顶紧并以局部承压传力。考虑到梁端支座反力偏心的不利影响，承托与柱的连接焊缝按1.25倍梁端支座反力来计算。为了便于安装，梁端与柱侧面应预留5～10mm的间隙，安装时加填板并设置构造螺栓，以固定梁的位置。当两相邻梁的支座反力相差较大时，应考虑偏心影响，对柱身应按压弯构件进行验算。

5.7.2.2　梁与柱的刚性连接

框架梁与柱的连接节点做成刚性连接，可以增强框架的抗侧移刚度，减小框架横梁的跨中弯矩。在多、高层框架中梁与柱的连接节点一般都是采用刚性连接。梁与柱节点的刚性连接就是要保证将梁端的弯矩和剪力可以有效地传给柱子。图5-28是梁与柱的刚性连接构造图。

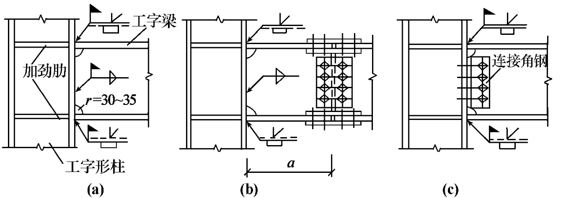
图5-28　梁与柱的刚性连接

图5-28（a）所示为多层框架工字形梁和工字形柱全焊接刚性连接。梁翼缘与柱翼缘采用坡口对接焊缝连接。为了便于梁翼缘处坡口焊缝的施焊和设置衬板，在梁腹板两端上、下角处各开r=30～35 mm的半圆孔。梁翼缘焊缝承受由梁端弯矩产生的拉力和压力；梁腹板与柱翼缘采用角焊缝连接以传递梁端剪力。这种全焊接节点的优点是省工省料，缺点是梁需要现场定位、工地高空施焊，不便于施工。为了消除上述缺点，可以将框架横梁做成两段，并把短梁段在工厂制造时先焊在柱子上，如图5-28（b）所示，在施工现场再采用高强度螺栓摩擦型连接将横梁的中间段拼接起来。框架横梁拼接处的内力比梁端处小，因而有利于高强度螺栓连接的设计。图5-28（c）为梁腹板与柱翼缘采用连接角钢和高强度螺栓连接，并利用高强度螺栓兼作安装螺栓。横梁安装就位后再将梁的上、下翼缘与柱的翼缘用坡口对接焊缝连接。这种节点连接包括高强度螺栓和焊缝两种连接件，要求它们联合或分别承受梁端的弯矩和剪力，常称为混合连接。

图5-29（a）为工字形梁与柱的刚性连接节点（柱腹板内不设横向加劲肋的刚性节点）的变形示意图。在梁的受压翼缘处［图5-29（b）］，由梁端弯矩引起的集中压力对柱腹板产生挤压力，应验算:柱腹板计算高度边缘处的局部承压强度以及柱腹板在横向压力作用下的局部稳定；在梁受拉翼缘的拉力作用下［图5-29（c）］，防止柱翼缘发生横向变形过大，保证梁翼缘应力均匀分布，应验算柱翼缘的厚度。

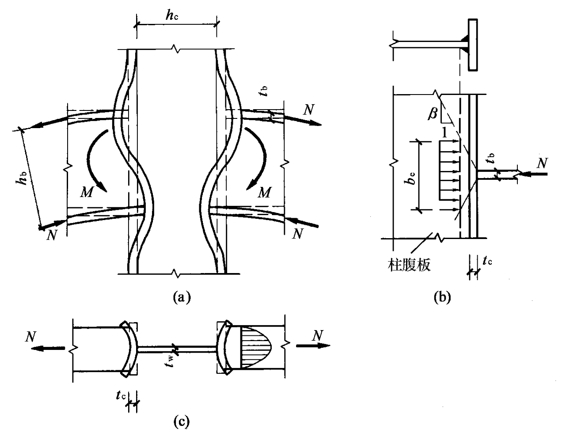
图5-29　梁柱节点的变形和柱腹板的受力

在梁的受压翼缘处，柱腹板的厚度t_w应同时满足:局部承压条件:

局部稳定条件:

在梁的受拉翼缘处，柱翼缘板的厚度t_c按强度计算应满足:

式中，A_fc、A_ft分别为梁受压、受拉翼缘的截面面积；f_c、f_b分别为柱、梁钢材抗拉（压）强度设计值；b_e为在垂直于柱翼缘的集中压力作用下，柱腹板计算高度边缘处压应力的假定分布长度，参照规范梁中局部承压Lz的公式计算；h_c为柱腹板的宽度；f_fy为柱钢材屈服点。

如果上述关于梁的受压或受拉翼缘处的计算不能满足，就需要对柱的腹板设置横向（水平）加劲肋。梁与柱刚性连接中柱腹板横向加劲肋的尺寸要求应满足《钢结构设计规范》中7．4．3条的有关规定。

梁与柱刚性连接节点的节点域如图5-30（a）所示，由柱的翼缘板和腹板的横向加劲肋所包围，即节点域的边长分别是梁和柱的腹板高度。节点域在周边剪力和弯矩作用下，柱腹板存在屈服和局部失稳的可能性，应验算其抗剪强度和稳定性节点域在梁端弯矩作用下将产生较大的剪力。设梁端弯矩仅由梁翼缘板承受，柱腹板上边加劲肋受力如图5-30（b）所示，则有:

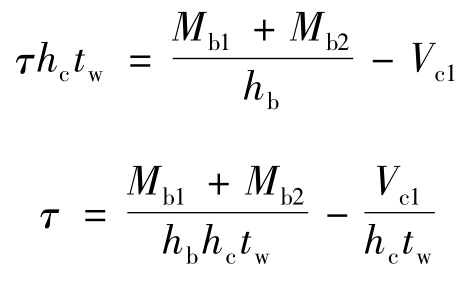
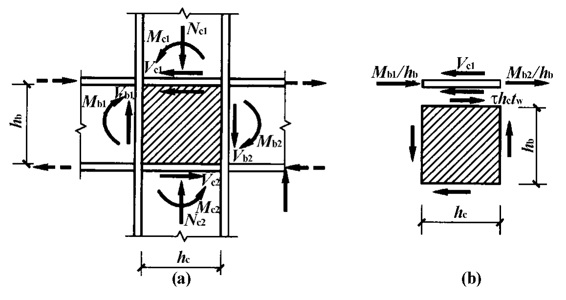
图5-30　梁与柱刚性连接的节点域

节点域中的应力比较复杂，剪应力τ在节点域的中心为最大，剪切屈服由中心开始逐步向四周扩展。由于节点域四周有较强的弹性约束，节点域屈服后，剪切承载力仍可提高。试验证明:节点域的剪应力τ达到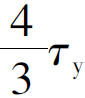时，节点域仍能保持稳定，因此将节点域屈服剪应力提高到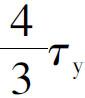。即节点域抗剪屈服条件为: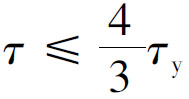。忽略柱剪力V_c1及柱轴力的影响，节点域抗剪强度按下式验算:

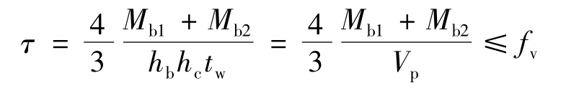
或

式中，M_b1、M_b2分别为节点两侧梁端弯矩设计值；f_v为钢材抗剪强度设计值；h_b、h_c分别为梁和柱的腹板高度；t_w为柱腹板厚度；V_p为节点域腹板的体积，柱为工字形截面时，V_p=h_bh_ct_w；柱为箱形截面时，V_p=1.8h_bh_ct_w。

当柱承受较大的压力N_c时，应将f_v乘以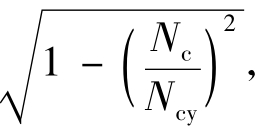以考虑柱压力N_c对节点域抗剪承载力的影响，式中N_cy为柱的屈服轴压承载力。

为了防止节点域的柱腹板受剪时发生局部失稳，节点域内柱腹板的厚度t_w应满足下式要求:

式中，h_c、h_b分别为柱和梁的腹板高度。

当柱腹板节点域不满足抗剪强度的要求时，柱腹板应予补强。如图5-31所示，对焊接H形组合柱，宜将柱腹板在节点域范围内更换为较厚板件。加厚板件应伸出柱上、下横向加劲肋（即梁上、下翼缘高度处）之外各150mm，并采用对接焊缝将其与上、下柱腹板拼接。

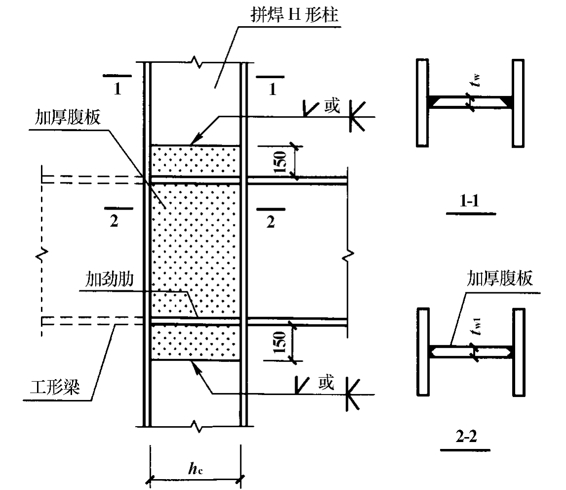
图5-31　节点域腹板的加厚

5.7.2.3　梁与柱的半刚性连接

图5-32为多层框架梁与柱的半刚性连接节点。

在图5-32（a）中，梁端上、下翼缘处各用一个角钢作为连接件，并采用高强度螺栓摩擦型连接将角钢的两肢分别与梁和柱连接，这种连接属于半刚性连接。图5-32（b）为梁端焊一端板，端板用高强度螺栓与柱翼缘连接，常称为端板连接。试验结果表明:图5-32（b）比图5-32（a）的转动刚度大，当图5-32（b）中的连接端板足够厚且螺栓布置合理、数量足够时，端板连接对梁端的约束可以达到刚性连接的要求。

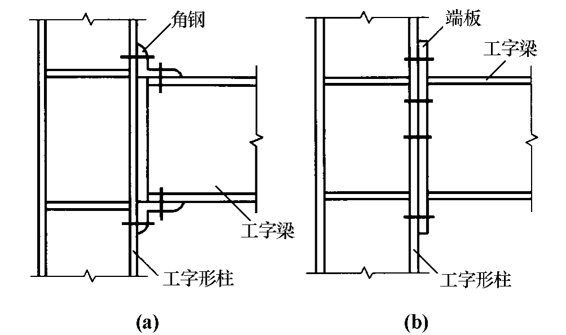
图5-32　梁与柱的半刚性连接(www.daowen.com)

图5-33为轻型单层框架梁与柱连接的常见节点形式，属于半刚性连接节点。斜梁端板有三种形式:端板竖放［图5-33（a）］、端板斜放［图5-33（b）］和端板平放［图5-33（c）］。与图5-32（b）端板连接类似，当斜梁端板的厚度足够厚且螺栓布置合理、数量足够时，图5-33所示的端板连接可以作为刚性连接。

半刚性连接的框架计算比较复杂，需要通过试验确定节点连接的M –θ关系曲线。目前，关于半刚性连接已取得许多研究成果，但尚未达到实用化程度。

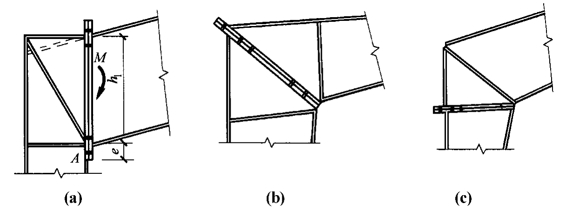
图5-33　刚架斜梁与柱的连捧

5.7.3　柱脚节点

5.7.3.1　柱脚的形式与构造

柱脚（Columnbases）的作用是将柱的下端固定于基础，并将柱身所受的内力传给基础。基础一般由钢筋混凝土做成，其强度远比钢材低。为此，需要将柱身的底端放大，以增加其与基础顶部的接触面积，使接触面上的压应力小于或等于基础混凝土的抗压强度设计值。柱脚按其与基础的连接方式不同，可分为铰接和刚接两种型式。

图5-34是几种常用的铰接柱脚型式，主要用于轴心受压柱。图5-34（a）在柱子下端直接与底板焊接。柱子压力由焊缝传给底板，由底板扩散并传给基础。由于底板在各方向均为悬臂，在基础反力作用下，底板抗弯刚度较弱，所以这种柱脚型式只适用于柱子轴力较小的情况。当柱子轴力较大时，通常采用图5-34（b）、（c）、（d）所示的柱脚型式。在柱子底板上设置靴梁、隔板和肋板，底板被分隔成若干小的区格。底板上的靴梁、隔板和肋板相当于这些小区格板块的边界支座，改变了底板的支承条件。在基础反力作用下，底板的最大弯矩值变小了。柱子轴力通过竖向角焊缝传给靴梁，靴梁再通过水平角焊缝传给底板。图5-34（b）中，靴梁焊在柱翼缘的两侧，在靴梁之间设置隔板，以增加靴梁的侧向刚度；同时，底板被进一步分成更小的区格，底板中的弯矩也因此而减小。图5-34（c）是格构柱仅采用靴梁的柱脚型式。图5-34（d）在靴梁外侧设置肋板，使柱子轴力向两个方向扩散，通常在柱的一个方向采用靴梁，另一方向设置肋板，底板宜做成正方形或接近正方形。此外，在设计柱脚中的连接焊缝时，要考虑施焊的方便与可能性。

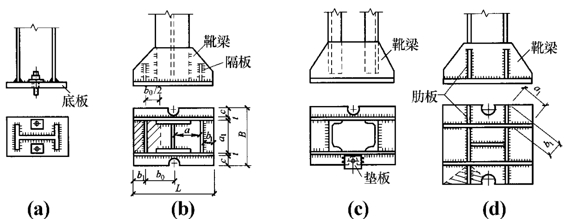
图5-34　铰接柱脚

图5-35是常用的刚接柱脚型式，主要用于框架柱（压弯构件）。图5-35（a）是整体式刚接柱脚，用于实腹柱和支间距离小于1.5m的格构柱。当格构柱支间距离较大时，采用整体式柱脚是不经济的，这时多采用分离式柱脚，如图5-35（b）所示，每个分支下的柱脚相当于一个轴心受力铰接柱脚，两柱脚之间用隔材联系起来。

柱脚通过预埋在基础上的锚栓来固定，锚栓按柱脚是铰接还是刚接进行布置和固定。铰接柱脚只沿着一条轴线设置两个连接于底板上的锚栓（图5-34），锚栓固定在底板上，对柱端转动约束很小，承受的弯矩也很小，接近于铰接。底板上的锚栓孔的直径应比锚栓直径大0.5～1.0倍，并做成U形缺口，待柱子就位并调整到设计位置后，再用垫板套住锚栓并与底板焊牢。在铰接柱脚中，锚栓不需计算。

刚接柱脚中，靴梁沿柱脚底板长边方向布置，锚栓布置在靴梁的两侧，并尽量远离弯矩所绕轴线。锚栓要固定在柱脚具有足够刚度的部位，通常是固定在由靴梁挑出的承托上。在弯矩作用下，刚接柱脚底板中拉力由锚栓来承受，所以锚栓的数量和直径需要通过计算决定。靴梁在柱脚弯矩作用下变形很小，能够传递弯矩，符合刚接柱

脚的要求。为了便于柱子的安装，锚栓不宜穿过柱脚底板。

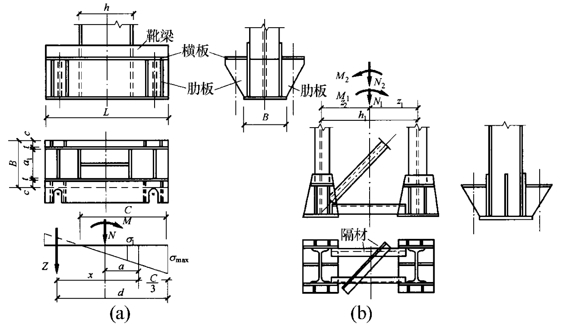
图5-35　刚接柱脚

柱脚的剪力主要依靠底板与基础之间的摩擦力来传递。当仅靠摩擦力不足以承受水平剪力时，应在柱脚底板下面设置抗剪键，如图5-36所示，抗剪键可用方钢、短T形钢做成。也可将柱脚底板与基础上的预埋件用焊接连接。

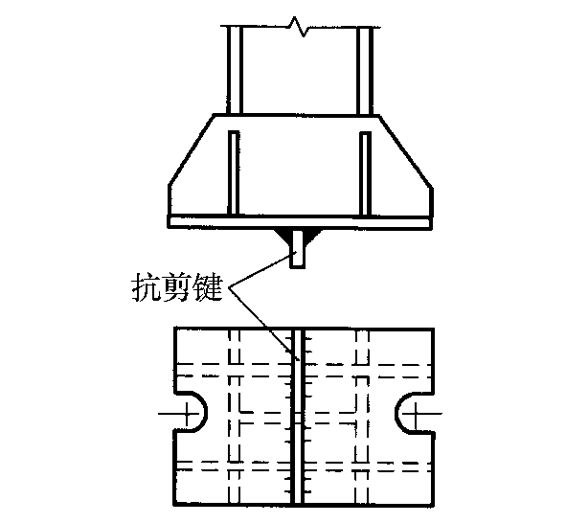
图5-36　柱脚的抗剪

近年来一种将钢柱直接插入混凝土基础杯口内，用二次浇注混凝土将其固定的插入式柱脚形式，已在多项单层工业厂房工程中应用，效果较好。这种柱脚构造简单，节约钢材，安装调整快捷，安全可靠，已列入《钢结构设计规范》的第八章8.4节。

5.7.3.2　轴心受压柱的柱脚计算

1．底板的计算

底板的平面尺寸取决于基础材料的抗压能力，假设基础对底板的压应力是均匀分布的，则底板的面积［见图5-34（b）］按下式计算:

式中，L、B分别为底板的长度和宽度；N为柱的轴心压力；f_c为基础所用混凝土的抗压强度设计值；A₀为锚栓孔的面积。

根据构造要求定出底板的宽度:

式中，a₁为柱截面已选定的宽度或高度；t为靴梁厚度，通常取10～14 mm；c为底板悬臂部分的宽度，通常取锚栓直径的3～4倍；锚栓常用直径为20～24 mm。

底板的长度为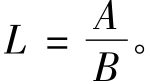底板的平面尺寸L、B应取整数。根据柱脚的构造型式，可以取L与B大致相同。

底板的厚度由板的抗弯强度决定。可以把底板看作是一块支承在靴梁、隔板、肋板和柱端的平板，承受从基础传来的均匀反力。靴梁、隔板、肋板和柱端面看作是底板的支承边，并将底板分成不同支承形式的区格，其中有四边支承、三边支承、两相邻边支承和一边支承。在均匀分布的基础反力作用下，各区格单位宽度上最大弯矩为:

四边支承板最大弯矩为:

三边支承板及两相邻边支承板最大弯矩为:

一边支承（悬臂）板最大弯矩为:

式中，q为作用于底板单位面积上的压力；a为四边支承板中短边的长度；α为系数，由板的长边b与短边a之比，查表5-12；a₁为三边支承板中自由边的长度；两相邻支承板中对角线的长度［见图5-34中（b）、（d）］；β为系数，由b₁/a₁，查表5-13，b₁为三边支承板中垂直于自由边方向的长度或两相邻边支承板中的内角顶点至对角线的垂直距离［见图5-34中（b）、（d）］。当三边支承板b₁/a₁小于0.3时，可按悬臂长为b₁的悬臂板计算；c为悬臂长度。

表5-12　四边支承板弯矩系数α

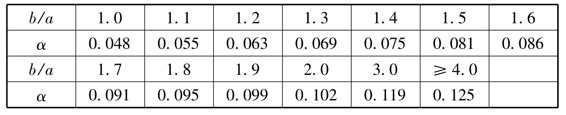
表5-13　三边支承板及两相邻边支承板弯矩系数β

经过计算，取各区格板中的最大弯矩M_max，按公式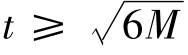来确定底板的厚度t。合理的设计应使各区格板的弯矩值基本相近，如果区格板的弯矩值相差很大，则应调整底板尺寸或重新划分区格。

为了使底板具有足够的刚度，以满足基础反力均匀分布的假设，底板厚度一般为20～40mm，最小厚度不宜小于14mm。

2．靴梁的计算

在柱脚制造时，柱身往往做得稍短一些［见图5-34（c）］，在柱身与底板之间仅采用构造焊缝相连。在焊缝计算时，假定柱端与底板之间的连接焊缝不受力，柱端对底板只起划分底板区格支承边的作用。柱压力N是由柱身通过竖向焊缝传给靴梁，再传给底板。焊缝计算包括:柱身与靴梁之间竖向连接焊缝承受柱压力N作用的计算；靴梁与底板之间水平连接焊缝承受柱压力N作用的计算。同时要求:每条竖向焊缝的计算长度不应大于60h_f。

靴梁的高度根据靴梁与柱身之间的竖向焊缝长度来确定，其厚度略小于柱翼缘板厚度。在底板均布反力作用下，靴梁按支承于柱侧边的双悬臂简支梁计算。根据靴梁所承受的最大弯矩和最大剪力，验算其抗弯和抗剪强度。

3．隔板、肋板的计算

隔板应具有一定的刚度，才能起支承底板和侧向支撑靴梁的作用。为此，隔板的厚度不得小于宽度的1/50，且厚度不小于10mm。

隔板按支承在靴梁侧边的简支梁计算，承受由底板传来的基础反力作用，荷载按图5-34（b）所示阴影面积的底板反力计算。根据其承受的荷载，计算隔板与底板之间的连接焊缝（隔板内侧不易施焊，仅有外侧焊缝），验算隔板强度，计算隔板与靴梁之间的焊缝。隔板的高度由其与靴梁连接的焊缝长度决定。

肋板按悬臂梁计算，荷载按图5-34（d）所示的阴影面积的底板反力计算，应计算肋板及其连接的强度。

5.7.3.3　框架柱的柱脚计算

框架柱多采用刚接柱脚。有时，单层框架也采用铰接柱脚，其构造和计算与轴心受压柱的铰接柱脚相似。所不同的是铰接柱脚还要承受剪力。如果水平剪力超过底板与基础间的摩擦力，铰接柱脚一般要采取抗剪构造措施，如图5-36所示。

一、整体式柱脚1．底板的计算

图5-35（a）为整体式柱脚构造图。柱脚的传力过程与轴心受压柱脚类似，即柱子内力由柱身传给靴梁，再传至底板。但是，由于框架柱脚同时有弯矩和轴心压力作用，底板下的压力不是均匀分布的，并且可能出现拉力。如果底板下出现拉力，则此拉力由锚栓来承受。

假定柱脚底板与基础接触面的压应力成直线分布，底板下基础的最大压应力按下式计算:

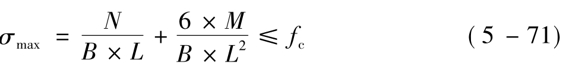
式中，N、M分别为使基础一侧产生最大压应力的内力组合值；B、L分别为底板的宽度、长度；f_c为混凝土的抗压强度设计值。

根据底板下基础的最大压应力不超过混凝土抗压强度设计值的条件，即可确定底板面积。一般先按构造要求决定底板宽度B，其中悬伸宽度c一般取20～30mm，然后求出底板的长度L。

底板厚度的计算方法与轴心受压柱脚相同。虽然底板各区格所承受的压应力不是均匀分布的，但是在计算各区格底板的弯矩值时，可以偏于安全地按该区格的最大压应力计算。底板的厚度一般不小于20mm。

2．锚栓的计算

底板另一侧的应力为:

当最小应力σ_max出现负值时，说明底板与基础之间产生拉应力。由于底板和基础之间不能承受拉应力，此时拉应力的合力由锚栓承担。根据对混凝土受压区压应力合力作用点的力矩平衡条件ΣM=0，可得锚栓拉力Z为:

式中，M、N分别为使锚栓产生最大拉力的内力组合值；a为柱截面形心轴到基础受压区合力点间的距离；x为锚栓位置到基础受压区合力点间的距离。

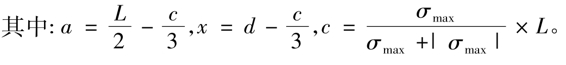
每个锚栓所需要的有效截面面积为:

式中，n为柱脚受拉侧锚栓数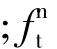为锚栓的抗拉强度设计值。

锚栓直径不小于20mm。锚栓下端在混凝土基础中用弯钩或锚板等锚固，保证锚栓在拉力Z作用下不被拔出。锚栓承托肋板按悬臂梁设计，高度一般不小于350～400mm。

3．靴梁、隔板、肋板及其连接焊缝的计算

柱身与靴梁连接焊缝承受的最大内力N₁按下式计算:

靴梁的高度由靴梁与柱身之间的焊缝长度确定，其高度不宜小于450mm。靴梁按双悬臂简支梁验算截面强度，荷载按底板上不均匀反力的最大值计算。

靴梁与底板之间的连接焊缝按承受底板下不均匀基础反力的最大值设计。在柱身范围内，靴梁内侧不易施焊，故仅在靴梁外侧布置焊缝。

隔板、肋板及其连接的设计与轴心受压柱脚相似，只是荷载按底板下不均匀反力相应受荷范围的最大值计算。

二、分离式柱脚

图5-35（b）为分离式柱脚的构造图。这种柱脚可以认为是由两个独立的轴心受压柱脚所组成。每个分支的柱脚都是根据其可能产生的最大压力，按轴心受压柱脚进行设计。受拉分支的全部拉力由锚栓承担并传至基础。

分离式柱脚的两个独立柱脚所承受的最大压力为:

右支:

左支:

式中，N₁、M₁分别为使右支产生最大压力的柱内力组合值；N₂、M₂分别为使左支产生最大压力的柱内力合值；Z₁、Z₂分别为右支、左支至柱轴线的距离；h₁为两分支轴线距离。

每个柱脚的锚栓也按各自的最不利内力组合换算成的最大拉力计算。