5.5　结构的整体稳定与P-Δ效应

5.5.1　结构的整体稳定

5.5.1.1　结构的整体稳定性与二阶分析的概念

超高层建筑钢结构可以视为一个悬臂受压柱，不仅要通过控制板材的宽厚比与构件的长细比来保证构件的局部稳定性与整体稳定性，同时还需要考虑结构的整体稳定性。

对于多高层建筑钢结构，通常不会由于竖向荷载引起结构整体失稳。但高层钢结构的高宽比一般较大，当结构在风荷载或地震作用下产生水平位移时，竖向荷载产生的二阶效应将使结构的稳定问题比较突出，此时必须考虑位移产生附加水平力的影响。

当结构受到水平方向力的作用时将产生水平侧移，由于侧移引起竖向荷载的偏心又将产生附加弯矩，而附加弯矩又使结构的侧移进一步增大。对于非对称结构，平移与扭转耦联，当结构产生扭转时，竖向荷载的合力与抗侧力构件的轴线将产生偏心，从而也会引起附加的扭矩。这种由于竖向荷载作用于水平位移而产生的内力与侧移增大的现象称为P-Δ效应。如果由于侧移引起内力的增加最终能与竖向荷载相平衡的话，结构是稳定的，否则结构将出现P-Δ效应引起的整体失稳。

在进行多高层建筑结构第一阶段设计时，通常采用线弹性计算方法，此时在竖向荷载作用下与在水平荷载作用下的位移和内力是彼此独立的，两者的内力与位移可以直接相加，因而也称为一阶分析。由于P-Δ效应是在一阶侧移基础上产生的，所以又称为二阶效应，相应的计算分析称为二阶分析。

对于30层以下的多高层建筑，侧向刚度一般较大，P-Δ效应并不显著，通常可以忽略不计。然而，随着建筑层数的进一步增加以及建筑高宽比的增大，P-Δ效应造成的附加弯矩与附加位移所占的比例逐渐加大，对于50层左右的钢结构，P-Δ效应产生的二阶内力和位移可达15％以上。由此可见，对于超高层钢结构，如果不考虑二阶效应，可能造成一些构件实际负担的内力超过其设计承载力，从而引起结构的倒坍。

5.5.1.2　整体稳定性判断

“高钢规程”中规定，当高层建筑结构同时符合以下两个条件时，可不验算结构的整体稳定性。

1．结构各楼层柱的平均长细比和平均轴压比满足下式要求:

上式中，

λ_m——楼层柱的平均长细比；

N_m——楼层柱的平均轴压力设计值；

N_pm——楼层柱的平均全塑性轴压力，N_pm=f_yA_m，其中f_yA_m分别为钢材的屈服强度与柱截面面积的平均值。

2．结构按一阶线弹性计算所得的各楼层层间相对侧移值满足下式要求:

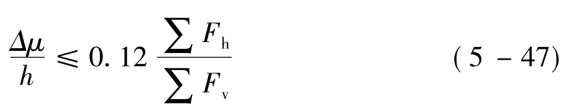
上式中，

h、Δμ——分别为楼层高度与质心处层间位移；

∑F_h、∑F_v——分别为计算楼层以上全部水平荷载之和与全部竖向荷载之和。

当不满足上述要求时，需要对整体稳定性进行验算。对于有支撑结构（钢支撑、剪力墙和核心筒等）且Δμ/h≤1/1000时，按有效长度法验算，柱的计算长度系数可按现行《钢结构设计规范》（GB50017）附录采用；对于无支撑的结构以及Δμ/h＞1/1000的有支撑结构，应按能反映P-Δ效应的方法验算结构的整体稳定。

5.5.2　P-Δ效应的计算方法

P-Δ效应计算属于非线性问题，通常需要进行迭代计算。计算P-Δ的方法很多，这里只介绍其中两种有代表性的方法。

5.5.2.1　放大系数法

将高层建筑视为一个竖向悬臂构件，侧向承受均匀分布的水平力，在悬臂的自由端作用有竖向集中力P。此时，P-Δ效应引起的水平位移增大系数可用下式表示:

上式中，P_cr——使悬臂结构产生屈曲时作用于顶端的竖向集中力。

一阶分析与二阶分析位移的关系为

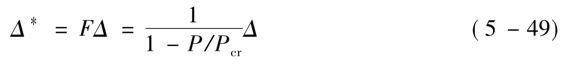
上式中，Δ^﹡、Δ分别为二阶分析与一阶线弹性分析的位移。

由于假定竖向荷载作用于结构的顶部，因而F为常数，从上至下水平位移增量的比例相同。在实际工程中，竖向荷载沿结构高度的分布是比较均匀的，考虑P-Δ效应后的总位移可以写为

其中，

P_o——沿高度均匀分布的竖向荷载；

P_ocr——均布竖向荷载作用下的屈曲临界值。(www.daowen.com)

同样，考虑P-Δ效应后的内力与一阶分析的内力M之间的关系为

屈曲荷载的临界值根据结构侧移曲线的不同，可以分别为剪切型、弯曲型与弯剪型等三种形式。

1．剪切型

对于框架结构，其侧向位移曲线呈剪切型变形，i层的临界荷载由下式确定:

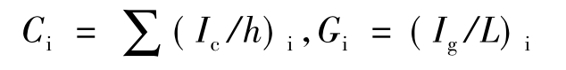
上式中，

C_i——i层所有柱的惯性矩与层高之比的总和；

G_i——i层所有梁的惯性矩与跨度之比的总和。

2．弯曲型

对于以剪力墙为主的结构，其侧向位移曲线呈弯曲型，屈曲荷载是截面惯性矩的函数。假定顶层的整体惯性矩是底部的1-β倍，则临界荷载为

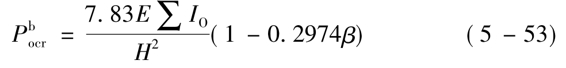
上式中，

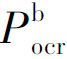——结构竖向荷载临界值；

H——结构的总高度；

∑I_o——基层所有柱对结构形心惯性矩之和。

3．弯剪型

对于框架—剪力墙结构，其侧移曲线呈弯剪型，在竖向均布荷载作用下，其临界荷载由下式确定

式中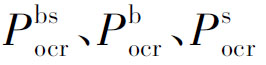，分别为弯剪型、弯曲型与剪切型侧移在结构底层的临界荷载。

5.5.2.2　数值迭代法

放大系数法求得的临界荷载通常精度较低，主要用于初步设计阶段。较为精确的P-Δ效应分析通常需要采用数值方法进行迭代计算。

假定作用于多高层建筑第i层的水平荷载为Q_i，产生的层间位移为δ_i，如图5-19所示。

为简单起见，假定柱的变形曲线沿层高算为直线，竖向荷载在柱底部产生的附加弯矩为P_iδ_i。为了计算方便，可以根据柱的平衡条件，利用在柱底引起相同弯矩的附加水平剪力来代替竖向荷载，即

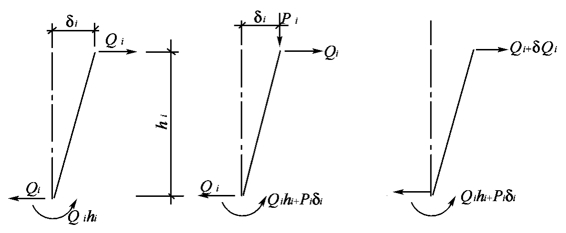
图5-19　将P-Δ效应等效为水平增量

第i层的等效剪力增量为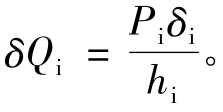图5-20为考虑相邻各层影响时的情况，在i层楼板处，水平荷载的增量为

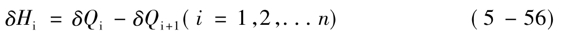
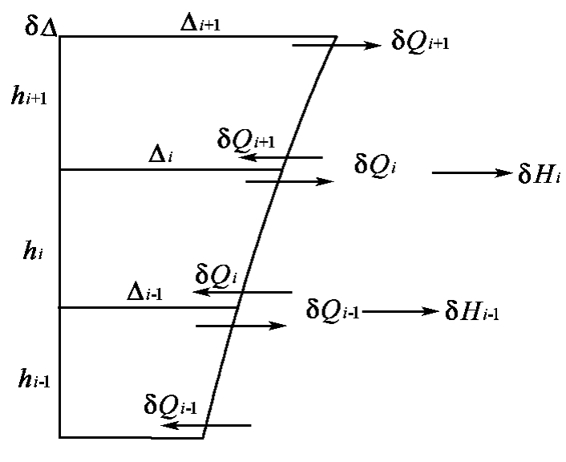
图5-20

将这一组附加的水平荷载增量作用于结构，即可得到考虑P-Δ效应的水平位移计算结果；检验计算结果是否收敛，如不满足精度要求，再进行下一轮计算，直至满足要求为止。为了加快迭代的收敛速度，可在等效剪力增量上乘一因子β，即

式中加速因子β一般可取1.1～1.2。