5.2　建立计算模型、选择计算方法及结构内力调整时需要注意的问题

5.2.1　建立合理的计算模型

多高层钢结构的抗震计算可采用平面抗侧力结构的空间协同计算模型。当结构布置规则、质量及刚度沿高度分布均匀且不计扭转效应时，可采用平面结构计算模型；当结构平面或立面不规则，体型复杂，无法划分平面抗侧力单元的结构，以及为筒体结构时，应采用空间结构计算模型。

5.2.1.1　楼板

在多高层钢结构中，绝大多数楼盖的做法是用圆头焊钉将压型钢板固定于钢梁的上翼缘，将压型钢板作为施工模板，现浇混凝土后形成钢筋混凝土组合楼盖体系。

与多高层钢筋混凝土结构类似，多高层钢结构的楼板通常在其自身平面内的刚度很大，因而在进行结构整体计算时，通常引入“楼板在平面内刚度无穷大、在平面外刚度为零”的假定。虽然楼板在其平面内绝对刚性的假定可以使结构分析得到极大的简化、计算量大为减少，但在对于某些复杂的结构进行分析时，却往往显得比较粗糙。比如在多高层钢结构中经常采用的腰桁架与帽桁架，由于其上、下弦杆均位于楼层平面内，如果采用刚性楼板假定，将无法得到弦杆的轴向力。此外，对于楼板上开大洞、建筑平面长宽比较大以及结构错层等情况，采用刚性楼板假定将导致很大的误差。所以，在建立力学模型时，需要考虑楼板的实际刚性。值得注意的是，将楼板作为弹性板壳单元参与结构整体计算时，应综合考虑压型钢板组合楼板的各向异性、折算厚度以及混凝土开裂等因素，对实际楼板的厚度应作适当的折减。同时，为了尽量缩短计算时间，节省计算机存储量，可以仅在需要考虑楼板变形的楼层或局部位置放置弹性板壳单元。

5.2.1.2　楼板与梁的共同工作

由于楼板与钢梁通过抗剪栓钉紧密地连接在一起，形成钢筋混凝土—钢组合梁，所以在进行结构整体计算时应该考虑现浇钢筋混凝土楼板与钢梁共同工作对结构刚度的影响。钢筋混凝土—钢组合梁的惯性矩，对两侧均有楼板的梁可取1.5I_b，对仅一侧有楼板的梁可取1.2I_b，其中I_b为钢梁的惯性矩。

进行多高层钢结构多遇地震作用下的反应分析时，可考虑现浇混凝土楼板与钢梁的共同作用。在设计中，应保证楼板与钢梁间有可靠的连接措施。此时楼板可作为梁翼缘的一部分来计算梁的弹性截面特性，楼板的有效宽度b_e按下式计算（图5-11）。

上式中，

b₀——钢梁上翼缘宽度；

b₁、b₂——梁外侧和内侧的翼缘计算宽度，各取梁跨度l的1/6和翼缘板厚度的6倍中的较小值。此外，b₁高不应超过翼板实际外伸宽度s₁；b₂不应超过相邻梁板托间净距s₀的1/2。

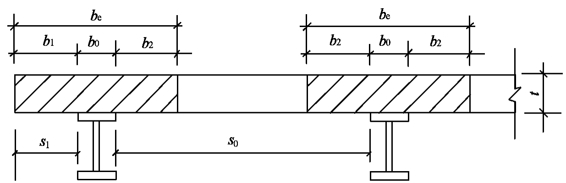
图5-11　楼板的有效宽度

进行多高层钢结构罕遇地震反应分析时，考虑到此时楼板与梁的连接可能遭到破坏，则不应考虑楼板与梁的共同作用。

5.2.1.3　梁、柱、墙

进行结构整体计算时，应考虑梁、柱的弯曲变形、剪切变形以及柱的轴向变形。由于框架梁与现浇钢筋混凝土楼板形成组合楼盖，梁的轴向力很小，一般可不考虑梁的轴向变形。当梁同时作为腰桁架或帽桁架的弦杆时，应计入轴向力的影响。在高层建筑钢结构中，柱的轴力通常很大，轴向变形的影响不能忽略。

对于带有现浇竖向连续的钢筋混凝土剪力墙或钢筋混凝土核心筒的钢框架结构，剪力墙既是竖向承重构件，也是结构中的主要抗侧力构件。剪力墙单元除应考虑墙板平面内的轴向变形、剪切变形与弯曲变形外，进行精确的结构分析时，最好还能反映剪力墙平面外刚度的影响。

5.2.1.4　梁柱节点

对于多高层建筑钢结构，框架梁柱节点域剪切变形（图5-12）对结构侧移的影响有时甚至可以超过10％～20％。节点域剪切变形对结构水平位移的影响主要取决于梁的抗弯刚度、节点域剪切刚度、梁腹板高度以及梁柱的刚度比。在进行结构整体计算时，虽然可以将梁柱节点作为一个单独的单元进行较为精确的分析，但通常是采用比较简单的办法近似考虑节点剪切变形的影响。对于采用箱型截面柱的框架，可将节点域作为刚域；刚域尺寸取节点域尺寸的一半。对于采用工字形截面柱的框架，假定刚域尺寸为零，梁、柱的长度取结构轴线尺寸，且当所考虑楼层的主梁线刚度平均值与节点域剪切刚度平均值之比EI_bm/（K_mh_bm）＞1或参数η＞5时，对所得的楼层侧移还需要作进一步修正。

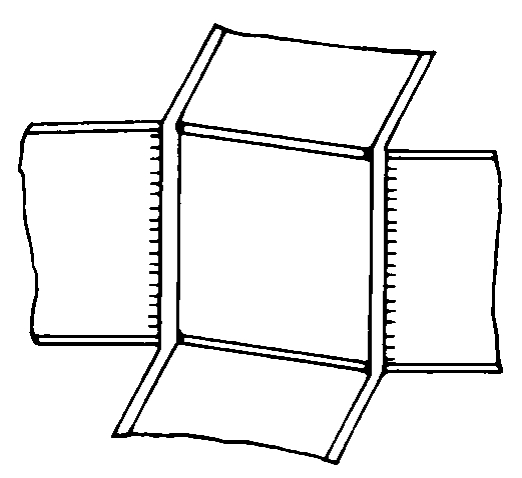
图5-12　节点域剪切变

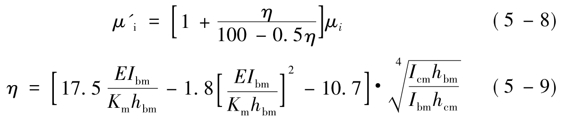
上式中，

μ'_i——修正后的第i层楼层的侧移；

μ_i——忽略节点域剪切变形并按结构轴线分析得到的第i层楼层的侧移；

I_cm、I_bm——分别为结构中柱和梁截面惯性矩的平均值；

h_cm、h_bm——分别为结构中柱和梁腹板高度的平均值；

K_m——节点域剪切刚度的平均值；

t_m——节点域腹板厚度平均值；

E、G——分别为钢材的弹性模量和剪切模量。

节点域剪切变形对结构内力的影响较小，一般在10％以内，通常不需对内力进行修正。分析结果还表明，对于带有支撑的框架结构，节点域剪切变形将随支撑体系侧向刚度的增加而迅速减小。

5.2.1.5　柱间支撑与耗能梁段

在高层钢结构设计中，柱间支撑斜杆的两端应为刚性连接，但在结构整体计算时可按两端铰接考虑，其端部连接的刚度则可通过支撑杆件的计算长度加以考虑。

偏心支撑的耗能段在大震时将首先屈服，由于它的受力性能不同，在建模时应将耗能梁段作为独立的梁单元处理。

5.2.1.6　装配嵌入式剪力墙

在多高层钢结构中，除了可以采用柱间支撑和现浇钢筋混凝土剪力墙作为结构抗侧力构件外，有时还可以采用装配嵌入式剪力墙提高结构的侧向刚度。常用的装配嵌入式剪力墙有钢板剪力墙、内藏钢板支撑剪力墙和带竖缝混凝土剪力墙等几种形式。在进行结构整体分析时，可按相同水平力作用下侧移相同的原则，将装配嵌入式剪力墙折算成等效剪切板，且通常只考虑其承受水平荷载产生的剪力，而不考虑其承受竖向荷载产生的压力。

一、钢板剪力墙

钢板剪力墙用钢板或带加劲肋的钢板制成，钢板墙的周边通过高强度螺栓与相邻的框架梁、柱相连接。在计算时可以忽略钢板墙平面内的正应力，而仅考虑其对结构抗剪强度的贡献。

1．不设加劲肋的钢板墙

对于不设加劲肋的钢板剪力墙，其受剪承载力V_y，由钢板的抗剪强度与稳定性决定。

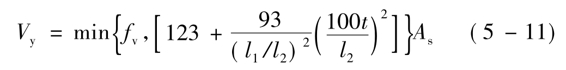
上式中，

f_v——钢板的抗剪强度设计值，抗震设防时应除以抗震调整系数0.9；

l₁、l₂——分别为所计算的柱和楼层梁所包围区格的长边和短边尺寸；

t——钢板的厚度；

A_s——墙板的受剪截面面积。

2．设有纵向与横向加劲肋的钢板剪力墙

对于如图5-13所示的设有纵向与横向加劲肋的钢板剪力墙，其受剪承载力V_y，由钢板的抗剪强度、局部稳定性及整体稳定性确定。

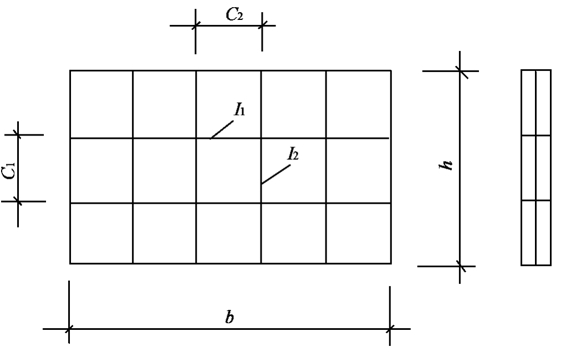
图5-13　带加劲肋的钢板剪力墙

上式中，

α——系数，非抗震时取1.0，抗震设防时取0.9；

C_l、C₂——分别为区格的长边和短边尺寸；

D₁、D₂——分别为两个方向加劲肋提供的单位宽度抗弯刚度，即

数值小者为D₂，大者为D₁。当墙板高宽比h/b小于1.0时需要式（5-12）的第三项。

钢板剪力墙的抗剪刚度K为

与钢板剪力墙受剪承载力V_y对应的侧移μ_y为

二、内藏钢板支撑剪力墙

内藏钢板支撑剪力墙是以钢板为基本支撑并外包钢筋混凝土墙板的预制构件。它通常只在支撑的端部与钢框架结构相连接，并且在混凝土墙板与周边框架梁、柱之间留有一定间隙。与普通钢支撑类似，内藏钢板支撑也有交叉支撑、人字支撑及单斜杆支撑等形式。其中，人字支撑最为常见。

内藏钢板支撑剪力墙的受剪承载力V_y，可按下式计算:

上式中，

n——支撑斜杆数，单斜杆支撑n=1，人字支撑和交叉支撑n=2；

A_br——支撑斜杆截面面积；

θ——支撑斜杆的倾角；

f——支撑钢材的抗拉、抗压强度设计值。

钢板屈服前内藏钢板支撑剪力墙的抗剪刚度K₁可近似地按下式计算:

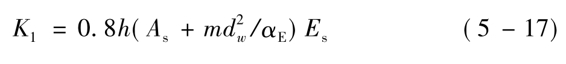
上式中，

h——装配嵌入式墙板的高度；

A_s——钢板截面积；

m——墙板有效宽度系数，单斜杆支撑为1.08，人字支撑及交叉支撑为1.77；

d_w——墙板厚度；

αE——钢与混凝土弹性模量之比。

与内藏钢板支撑剪力墙受剪承载力V_y相对应的侧移μ_y为

支撑钢板屈服后，内藏钢板支撑剪力墙的侧向刚度K₂可近似取K₁的十分之一，即

内藏钢板支撑剪力墙的水平剪力与侧移的关系曲线如图5-14所示。

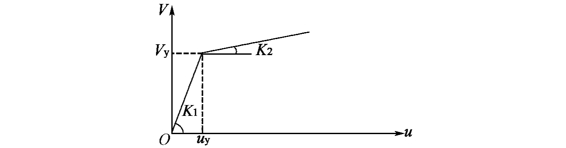
图5-14　内藏钢板支撑剪力墙水平剪力与侧移的关系

三、带竖缝混凝土剪力墙

带竖缝混凝土剪力墙板安装时与框架柱间留有一定空隙，墙板上端用高强度螺栓与框架梁下翼缘连接，墙板下端埋置在现浇混凝土楼板内，通过齿槽和钢梁上焊钉实现可靠连接。

缝间墙纵筋屈服时带竖缝混凝土剪力墙（如图5-15所示）的受剪承载力V_yl可按下式计算:

上式中，

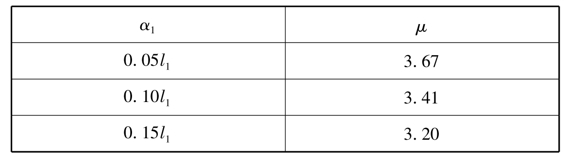
μ——系数，按表5-8采用；

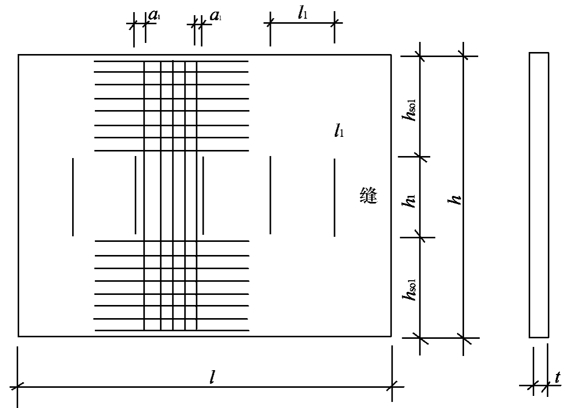
图5-15　带竖缝的混凝土剪力墙

l₁、h₁——分别为竖缝的间距与竖缝的高度；

f_shy——水平横向钢筋的抗拉强度设计值；

A_s——缝间墙所配纵筋截面面积。

表5-8　系数μ值

缝间墙纵筋屈服前墙板的侧向刚度由下式确定:

其中

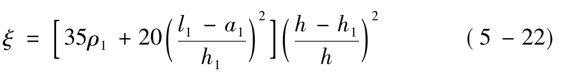
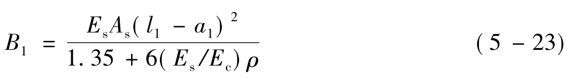
上式中，

ξ——考虑剪切变形影响的刚度修正系数；

B₁——缝间墙抗弯刚度；

ρ、ρ₁——分别为缝间墙配筋率与截面配筋系数。

缝间墙纵筋屈服时墙板的侧移μ_y为

缝间墙受弯破坏时的最大抗剪承载力V_μ为

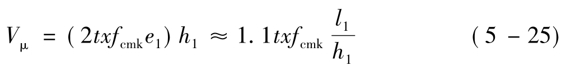
上式中，

e₁——缝根截面的约束力偏心矩，e₁=l₁/1.8；(www.daowen.com)

x——缝根截面的缝间墙混凝土受压区高度，即

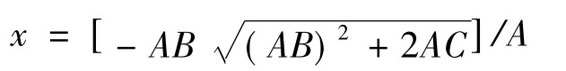
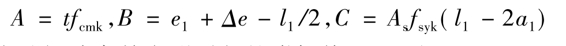
Δ_e——由缝间墙弯剪变形引起的附加偏心距，取Δ_e=0.003h；

f_cmk——混凝土弯曲抗压强度标准值。

此时侧向刚度K₂可近似取K₁的20％，即

与最大抗剪承载力V_μ相应的侧移μ_μ为

带竖缝混凝土剪力墙板的极限侧移量μ_max可按下式确定:

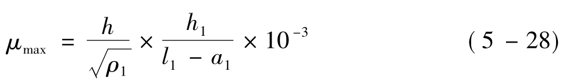
带竖缝混凝土剪力墙的水平剪力与侧移的关系曲线如图5-16所示。

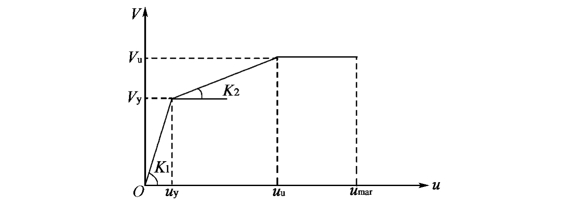
图5-16　带竖缝混凝土剪力墙的水平剪力与侧移的关系

5.2.1.7　非结构构件

在多高层建筑中存在着诸如围护结构、内隔墙等大量非结构构件。由于在整体计算模型中通常只，考虑非结构构件的荷载效应而不计入其对结构刚度的影响，所以计算所得的周期往往比实际结构的周期长。为了比较准确地计算实际结构在地震作用下的效应，应对主体结构计算所得的周期乘以考虑非结构构件影响的修正系数。《高层民用建筑钢结构技术规程》（JGJ99-98）建议修正系数采用0.9，设计人员也可根据主体结构的形式与采用非结构构件的具体情况加以调整。

5.2.2　平面协同与三维空间矩阵位移法

在进行多高层建筑钢结构分析时，可采用平面抗侧力结构的空间协同计算模型。当结构布置规则，质量与刚度沿高度分布均匀，且无扭转效应时，可采用平面结构计算模型；当结构的平面或立面不规则，体型复杂，无法划分成平面抗侧力单元，或为筒体结构时，应采用三维空间结构计算模型。

5.2.2.1　平面协同矩阵位移法

平面布置规则的框架—支撑结构和框架-剪力墙结构，在水平荷载作用下可以近似地简化为平面抗侧力体系，将沿主轴方向或斜交方向的所有框架合并为总框架，并将所有竖向支撑合并为总支撑，将所有剪力墙合并为总剪力墙，然后进行协同工作分析，参见图5-17。

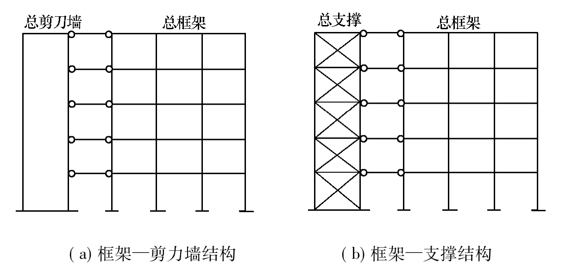
图5-17　结构的平面协同法

当进行简化计算时，总支撑可视为一根竖向弯曲杆件，其等效惯性矩I_eq为

上式中，

μ——折减系数，对中心支撑可取0.8～0.9；

A_ij——第j榀竖向支撑第i根柱的截面面积；

a_ij——第i根柱至第j榀竖向支撑的柱截面形心轴的距离；

n——每一榀竖向支撑的柱子数；

m——水平荷载作用方向竖向支撑的榀数。

5.2.2.2　三维空间矩阵位移法

随着多高层建筑的平面形状与体型日益复杂化，出现了大底盘多塔楼、顶部连体等复杂的结构体系，结构平动与扭转的耦联效应往往不能忽略，此时已经很难再将结构的抗侧力构件沿某几个方向进行分解，平面协同法的应用受到很大的限制。

与平面协平法相比，三维空间矩阵位移法对结构的布置和体型几乎没有限制，所以在目前实际多高层建筑结构设计计算中，绝大部分采用了三维空间矩阵位移法。

5.2.3　二阶段设计中的抗震验算

根据“高钢规程”（JGJ99-98）的规定，高层建筑钢结构的抗震设计应采用两阶段设计法。第一阶段为多遇地震作用下的弹性分析，主要验算构件的承载力、稳定性及结构的层间位移；第二阶段为罕遇地震作用下的弹塑性分析，主要验算结构的屈服机构、层间位移和层间位移延性比。

5.2.3.1　第一阶段抗震设计

结构在第一阶段多遇地震作用下的抗震设计中，其地震作用效应采用弹性方法计算。可根据建筑的高度与体型的复杂程度，采用底部剪力法、振型分解反应谱法以及时程分析法。

1．高度不超过40m且平面和竖向较规则的、以剪切变形为主的建筑，可采用底部剪力法计算，地震作用按现行国家标准《建筑抗震设计规范》（GBJ50011—2001）规定的地震作用确定。

2．高度不超过60m且平面和竖向比较规则的建筑，也可采用底部剪力法，但地震作用应根据“高钢规程”（JGJ99-98）确定。这是因为此时底部剪力法中已经近似考虑了部分高振型的影响。

3．高度超过60m的建筑，应采用振型分解反应谱法计算。

4．竖向特别不规则的建筑，宜采用时程法作补充计算。

需要指出的是，在上述各种算法中，振型分解反应谱法是最基本的方法，也是目前我国各种结构分析程序中的必备算法。

实测研究表明，钢结构房屋的阻尼比小于钢筋混凝土结构，对于超过12层的钢结构可采用0.002，对于不超过12层的钢结构可采用0.035，对于单层钢结构仍采用0.05。钢结构分析时，地震影响系数按表5-9的规定采用。

钢结构在进行内力和位移计算时，对于框架、框架—支撑、框架—抗震墙板以及框筒等结构常采用矩阵位移法，但计算时应计入重力二阶效应。对于工字形截面柱，宜计入梁柱节点域剪切变形对结构侧移的影响。对中心支撑框架和不超过12层的钢结构，其层间位移计算可不计入梁柱节点域剪切变形的影响。框架—支撑结构的斜杆可按端部铰接杆计算；中心支撑框架的斜杆轴线偏离梁柱轴线交点不超过支撑杆件的宽度时，仍可按中心支撑框架分析，但应计及由此产生的附加弯矩。

表5-9　水平地震影响系数最大值α_max

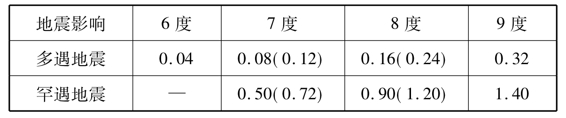
注:7度和8度时括号中数值分别用于设计基本地震加速度为0.15g和0.30g的地区。

对于简体结构，可将其按位移相等原则转化为连续的竖向悬臂简体，采用有限元法对其进行计算。

在预估杆截面时，内力和位移的分析可采用近似方法。在水平荷载作用下，框架结构可采用D值法进行简化计算；框架—支撑（抗震墙）可简化为平面抗侧力体系，分析时将所有框架合并为总框架，所有竖向支撑（抗震墙）合并为总支撑（抗震墙），然后进行协同工作分析。此时，可将总支撑（抗震墙）当作一悬臂梁。

5.2.3.2　第二阶段抗震设计

高层钢结构第二阶段的抗震验算应采用时程分析法对结构进行弹塑性时程分析，其结构计算模型可以采用杆系模型、剪切型层模型、剪弯型模型或剪弯协同工作模型。

在采用杆系模型分析时，柱、梁的恢复力模型可采用二折线型，其滞回模型可不考虑刚度退化。钢支撑和消能梁段等构件的恢复力模型，应按杆件特性确定。

采用层模型分析时，应采用计入有关构件弯曲、轴向力、剪切变形影响的等效层剪切刚度，层恢复力模型的骨架曲线可采用静力弹塑性方法进行计算，并可简化为二折线或三折线，并尽量与计算所得骨架曲线接近。层模型的计算精度虽然不如杆系模型，但计算量小、费用低、计算结果简明，能够从总体上把握结构在罕遇地震时的反应，因此在目前的实际工程设计中采用比较普遍。

在对结构进行静力弹塑性计算时，应同时考虑水平地震作用与重力荷载（不应计入风荷载）。并应考虑P-Δ效应对侧移的影响。构件所用材料的屈服强度和极限强度应采用标准值。

对新型、特殊的杆件和结构，其恢复力模型宜通过实验确定。分析时结构的阻尼比可取0.05，并应考虑二阶段效应对侧移的影响。

5.2.4　多遇地震作用下结构的内力调整

5.2.4.1　框架

在进行第一阶段抗震设计时，对于框架梁，可不按柱轴线处的内力而按梁端内力设计。框架—支撑结构或框架—剪力墙结构中总框架在任一楼层所承担的地震剪力，不得小于结构底部总剪力的25％和框架部分地震剪力最大值1.8倍二者的较小者。因为支撑和剪力墙是结构中的主要抗侧力构件，通常负担绝大部分水平地震力。如果在地震作用下支撑斜杆丧失稳定或剪力墙出现塑性铰，都将引起结构侧向刚度蜕化，使框架部分负担的地震剪力增大。为了确保多高层钢结构的安全，必须使框架部分的承载力具有一定的安全储备。人字形和U型支撑组合的内力设计值应乘以1.5的增大系数。

对于偏心支撑框架结构，为了确保消能梁段能进入弹塑性工作，消耗地震输入能量，支撑斜杆的轴力设计值，应取与支撑斜杆相连接的消能梁段达到受剪承载力时支撑斜杆轴力与增大系数的乘积，其值在8度及以下时不应小于1.4，9度时不应小于1.5；位于消能梁段同一跨的框架梁内力设计值，应取消能梁段达到受剪承载力时框架梁内力与增大系数的乘积，其值在8度及以下时不应小于1.5，9度时不应小于1.6；框架柱的内力设计值，应取消能梁段达到受剪承载力时柱内力与增大系数的乘积，其值在8度及以下时不应小于1．5，9度时不应小于1.6。

内藏钢支撑钢筋混凝土墙板和带竖缝钢筋混凝土墙板应按有关规定计算，带竖缝钢筋混凝土墙板可仅承受水平荷载产生的剪力，不承受竖向荷载产生的压力。钢结构转换层下的钢框架柱，地震内力应乘以1.5的增大系数。

在进行框架部分的内力计算时，应首先对其在地震作用下的内力进行调整，然后再与其他荷载产生的内力进行组合。在抗震设计中，一般高层钢结构可不考虑风荷载及竖向地震的作用，但对于高度大于60m的高层钢结构须考虑风荷载的作用，在9度区尚需考虑竖向地震的作用。

5.2.4.2　角柱、支撑柱

在结构平面的两个主轴方向分别计算水平地震效应时，角柱和两个方向的支撑或剪力墙所共有的柱，应考虑同时受双向地震作用的效应，其水平地震作用引起的构件内力应在进行总框架负担地震剪力不小于结构底部总剪力25％调整的基础上进一步提高30％。

5.2.4.3　托柱梁与托墙柱

在多遇地震作用下进行构件承载力计算时，托柱梁与承托钢筋混凝土抗震墙的钢框架柱的内力，应乘以增大系数1.5。

5.2.4.4　支撑斜杆

人字支撑、V形支撑的斜杆受压屈曲后，将使横梁产生较大变形，并使结构体系的侧向刚度发生蜕化，故此将人字支撑与V型支撑的斜杆内力放大1.5倍，以提高支撑的承载力。

十字交叉支撑、单斜杆支撑相应的内力增大系数为1.3。

5.2.4.5　支撑横梁

与人字支撑、V形支撑相交的横梁，在柱间的支撑连接处应保持连续。为了不增加人字支撑和V型支撑在竖向荷载作用下的负担，在设计人字支撑体系的横梁截面时，还需满足在不考虑支撑支点作用的情况下按简支梁跨中承受竖向集中荷载时的承载力。

5.2.4.6　支撑杆件的附加效应

1.P-Δ效应

多高层建筑钢结构的P-Δ效应是由两部分引起的，包括结构安装时的初始倾斜和水平荷载下楼层侧移的影响。在重力和水平力（风荷载和地震）作用下，支撑除作为竖向桁架的斜腹杆承受水平荷载引起的剪力外，还承受由水平位移与重力荷载产生的附加弯曲效应。在考虑由于P-Δ效应引起的附加效应时，楼层附加剪力V_i可按下式计算:

上式中，

Δμ_i——计算楼层的层间位移；

h_i——计算楼层的高度；

∑G_i——计算楼层以上的全部重力荷载。

上式中系数1.2反映了初始斜率和其他不利因素的影响。人字支撑和V形支撑还要考虑支撑跨梁传来的楼面垂直荷载。

2．柱压缩变形引起的附加压力

对于十字交叉支撑、人字支撑和V形支撑，柱在重力荷载作用下产生的弹性压缩变形在支撑斜杆中引起的附加压应力可按下列公式计算，对于十字交叉支撑的斜杆:

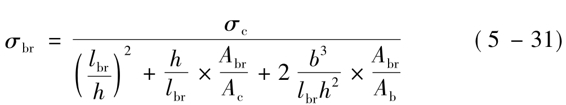
对于人字支撑和V形支撑的斜杆:

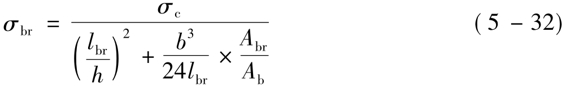
上式中，

σ_c——斜杆端部连接固定后，该楼层以上各层增加的恒荷载和活荷载产生的柱压应力；

l_br——支撑斜杆的长度；

b、I_b、h——分别为支撑跨梁的长度、绕水平主轴的惯性矩和楼层高度；

A_br、A_c、A_b——分别为计算楼层的支撑斜杆、支撑跨的柱和梁的截面面积。

在楼层刚度不大的情况下，柱压缩变形引起的附加应力对十字交叉支撑的影响比对人字支撑和V形支撑更为严重。

5.2.4.7　强柱弱梁

为使多高层钢结构在罕遇地震作用时形成梁屈服机构，应保证塑性铰出现在框架梁的端部。对于抗震设防的框架柱，在框架的任一梁、柱节点处，其截面的塑性抵抗矩与梁截面的塑性抵抗矩宜满足下式要求:

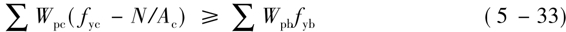
上式中，

W_pc、W_pb——分别为平面内交汇于节点的柱和梁的截面塑性抵抗矩；

f_yc、f_yb——分别为柱和梁钢材的屈服强度；

N——按多遇地震作用组合得到的柱轴力；

A_c——框架柱的截面面积。

在罕遇地震作用下，对于不可能出现塑性铰的部分，框架柱的轴力可由下式控制:

上式中，

f——柱钢材的抗压强度设计值，并除以构件承载力的抗震调整系数γ_RE。

5.2.4.8　偏心支撑柱

强柱弱梁的设计原则同样适用于偏心支撑框架。考虑到梁钢材的屈服强度有可能提高，为使塑性铰出现在梁而不是柱中，可将柱的设计内力适当提高。

偏心支撑柱的弯矩设计值M_c应按下列公式计算，并取其中的较小值:

偏心支撑柱的轴力设计值从应按下列公式计算，并取其中的较小值:

上式中，

V_p、V_lb——分别为耗能梁段的塑性受剪承载力与剪力设计值；

Mpc、M_lb——分别为耗能梁段在轴力作用下的全塑性受弯承载力与弯矩设计值；

Mc，com、N_c，com——分别为在竖向和水平荷载作用下考虑最不利组合时柱的弯矩和轴力。