附　录

第四部分定理证明过程

一、定理1和定理2证明

为证明当Znormal≥Z≥d时，运作成本存在最优解，我们需要证明单阶段服务型运作系统应急运作期望成本函数E［φ（u，r）｜Z≥d］是（u，r）的拟凸函数，因此，需要判断相应的海塞矩阵是否为正定或半正定矩阵。

进一步求（4－7）和（4－8）关于（u，r）的二阶偏导和联合偏导，如下：

设（u＊，r＊）是一阶条件（4－7）和（4－8）式为零时的解值。

由于（4－37）式的第一项是F（·）的减函数，第二项恒为正。因此，当u≤u＊，可知（4－37）式恒为非负。

令：

又P″（r）≥0，可知得当Znormal≥Z≥d，且u≤u＊时，E［φ（u，r）｜Z≥d］的海塞矩阵非负定，H≥0，此时，E［φ（u，r）｜Z≥d］为凸函数。

但Znormal≥Z≥d，u＞u＊时，由（4－37）式可知只有当（4－41）式成立时E［φ（u，r）｜Z≥d］才为凸函数。

事实上当u＞u＊，（4－41）式并不总能成立。

观察由一阶条件（4－7）式可知，当u＞u＊时，E［φ（u，r）｜Z≥d］是关于u的增函数，E［φ（u，r＊）｜Z≥d］表现为关于u的拟凸函数，并拥有唯一的谷点解为u＊。

为了更为清楚地描述该情况，我们将E［φ（u，r＊）｜Z≥d］的函数形式勾画如下：

由E［φ（u，r＊）｜Z≥d］的一阶条件（4－7）式可知，外购能力和内部能力恢复的结果是使得由此，可以得到：当Z≥d时，服务型运作系统单阶段期初计划投入的最优能力水平Z1＝F－1满足：

当Z＜d≤Znormal时，此时不需要外界能力支持u＊＝0，但系统内部仍然需要恢复能力，由（4－6）式得E［φ（Z，r）｜Z＜d］的一阶条件：

E［φ（Z，r）｜Z＜d］关于Z的二阶条件为：

因而可得：当Z＜d时，服务型运作系统单阶段期初投入的最优计划能力水平为，而由（4－2）可知Z2＝Znormal。

E［φ（Z，r）｜Z＜d］关于r的一阶条件

这里要考虑两种策略：若P′（Znormal－d）≤ω时采用r＊＝Znormal－d，显然系统最优的策略是采用“Order－Up－To”的能力恢复策略。否则r＊＝0，企业宁可承担损失也不去恢复能力，应急结束时运作系统持有的能力水平就是d。

二、定理3的证明

当Znormal≥Z≥d时，引入Lagrange函数

考虑Kuhn－Tucker一阶条件：

由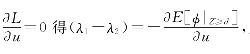又由Kuhn－Tucker一阶条件可得u（λ1－λ2）＋Sλ2＝0，得λ2代入λ2（S－u）＝0并结合（4－7）式，有：

可解得

讨论：若u＊≥S，则－u＊＝S，则λ1＝λ2＝0。

若0＜u＊＜S，则－u＊＝u＊，则λ1＝λ2＝0。

若u＊≤0，则－u＊＝0，则λ2＝0。由（4－7）式可知：只有当F（d＋r＊）因此取值受Z1限制。

由此可得同理可得R）｝。

同样可以证明，当Z＜d≤Znormal时的取值存在两种情况：

当P′（Znormal－d）≤ω时，－r＊＝min｛R，（Znormal－d）｝；或当P′（Znormald）＞ω时

三、定理6的证明

采用逆向归纳法证明。首先我们证明最后一个阶段的应急期望成本函数是关于IN的凸函数。由（4－28）式求关于IN的一阶和二阶偏导：

因此，单阶段应急运作的期望成本是IN的凸函数。接着假设从第n ＋1个阶段到应急结束时的最优总应急期望成本Tn＋1（In＋1）是凸函数，然后证明倒数第n个阶段的最优总应急期望成本Tn（In）是凸函数。

由（4－51）式可以证明a2　E［φ（un，rn，dn，In）］/a而由第n＋1个阶段开始到应急结束时的最优总应急成本关于In＋1是凸函数的假设，可知T″n＋1（·）≥0，由（4－51）式可以知a2　［Jn（un，rn，dn，In）］因此，当un和rn给定时，T″n（In）≥0。

四、定理7和定理8的证明对和求关于un和rn的二阶偏导和联合偏导，得

则倒数n个阶段期望总成本函数的海塞矩阵：

令是一阶条件式等于零的解，则由于F（·）是累积概率密度函数是关于un的增函数，进一步由定理6可知，T′n（·）是增函数，因此，当为非负定。

当时，我们并不能判断Hn是否为非负定函数。但我们观察到Jn（un，rn，dn，In）是关于un的一阶导数式，我们发现Jn（un，rn，dn，In）是关于un的增函数，因此是最优的决策。

因此，类似单阶段应急能力采购和能力恢复的结果，可得：当dn时，Jn（un，rn，dn，In）关于（un，rn）是一个拟凸函数。

进一步由式，可得和的表达式，如下：

第五章部分定理证明过程

一、定理2的证明

进一步求E［φ（r｜I）］关于r的二阶导数：

可以看出：（5－8）式的第二项、第三项、第四项和第五项均为非负，因此，只要：

即可保证进一步（5－19）≥αP′（r）＋α2（k－c1）－α2（h＋k），也即，若P′（r）≥α（h＋c1）。根据能力恢复成本不经济性的假设保证了运作系统能力恢复的边际成本P′（·）很大，一般P′（r）＞＞α（h＋c1），从而可以保证（5－19）式成立。

由此可以证明E［φ（r）］是凸函数。该阶段最优的能力恢复数量r＊＊为一阶条件（5－12）式的解，而进一步可以发现最优的外购能力数量符合“Order－Up－To”的订购策略，即u＊＊＝α（Znormal－I－d）－r＊＊。

进一步考虑外部能力供应和内部能力恢复数量存在上限约束，即u∈［0，S］、r∈［0，R］情况时的最优组合

引入Lagrange函数L（u，r）＝E［φ（r）］＋λ1u＋λ2（S－u）＋λ3r＋λ4 （R－r），并考虑其Kuhn－Tucker一阶条件，可以求得r可行解为0、r＊＊和R，u的可行解为0、u＊＊和S。综合可行解，可得约束情况下的最优外购能力和内部能力恢复数量为＝max｛0，min（r＊＊，R）｝和＝max｛0，min［α（Znormal－d）－r＊＊，S］｝。

二、定理3的证明

采用逆向归纳法证明。首先证明最后一个阶段的风险态度因子影响下的成本函数TN（IN）是关于IN的凸函数。

首先求TN（IN）关于IN的一阶导数：

将（5－20）式进一步展开，得：

令G＝G（uN），

F＝F［αZnomal＋（1－α）（IN＋dN）］；

π＝代入（5－21）式进一步化简得：

由此可知：当h－（h＋k）时，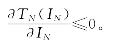

进一步化简：

也即令运作系统计划投入的能力水平则当Z≥ Z1时，TN（IN）是一个递减函数。

进一步求TN（IN）关于rN的二阶导数：

由（5－23）式可知，当时，是关于IN的凸函数。而也就说引入风险态度因子α后，存在另一个能力投入水平Z2。也即当Z≤Z2时

接着假设从第n＋1个阶段到应急结束时的最优总应急成本Tn＋1 （In＋1）是凸函数，然后证明从第n个阶段到应急结束时的最优总应急成本Tn（In）是凸函数。

其中T′n＋1（x，y）＝T′n＋1（max（0，In＋x＋dn＋rn－y））

由（5－23）可知，当时，若进一步满足h－（h＋k（x）dx≤0，则Jn（rn｜α，dn，In）是关于In的凸函数，即≥0。(www.daowen.com)

综上所述：

当Z1≤Zn≤Z2时，Tn（In）是关于In的凸函数。

定理4的证明：

求Jn（rn｜α，dn，In）关于rn的二阶导数为：

根据定理3的结论，可知当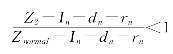时，Jn（rn｜α，dn，In）是关于rn的凸函数，则存在唯一的｛rn｝序列使得生产型运作系统的多阶段能力采购和恢复的应急总成本最优。其中是（5－17）为零时的解。

进一步可以考虑rn存在上限约束时的解序列，则而采购决策序列可通过“Order－Up－To”的策略得到。

第六章部分定理证明过程

一、证明（t）是关于t的凸函数

（1）若t≥0，则L（xL（t）关于t的一阶导数进一步L（t）关于t的二阶导数为：因此，当t≥0时，L（t）是关于t的凸函数；

（2）若t＜0，则

L（t）关于t的一阶导数关于t的二阶导数

则综合上述证明可得L（t）是关于t的凸函数，且连续可微。

二、定理1的证明

证明定理1是关于x的凸函数。

证明：采用逆向归纳法证明。本处证明仅考虑应急阶段期初计划投入能力水平大于零时的情况，阶段期初投入能力水平小于零时的证明类似。

首先证明最后一个阶段的应急期望成本函数是关于xN，m的凸函数。由于最后一个阶段应急结束时运作系统自身持有能力恢复至Znormal，则在第（N，m）个阶段结束时，运作系统不发出正常和快速采购的订单。

为后续推倒的公式简洁，省略了（6－23）等式右边的下标：

则TN，m（x）关于x的一阶偏导：

进一步求TN，m（x）关于x的二阶偏导：

因此，第（N，m）个阶段的应急运作成本是x的凸函数。

当j＝τ＋1，…，m－1时，假设TN，j＋1（x）是关于x的凸函数，然后证明TN，j（x）是关于x的凸函数，由于正常订单已经到达运作系统，所以此后阶段内无uN。因此，折现的总期望成本，如下：

求（6－27）式JN，j（x，z，v）关于x的一阶偏导数：

进一步求JN，j（x，z，v）关于x的二阶偏导数：

由于TN，j＋1（x）关于x为凸函数的假设，则T″N，j＋1（x＋z＋v－y）≥0，又f（·）≥0，则由（6－29）式可得因此，当z，v取最优值时，T″N，j（x）≥0，从而可得TN，j（x）是关于x的凸函数。

接着证明j＝τ时，TN，τ（x）是关于x的凸函数，由于前述的证明可知，TN，τ＋1（x）是凸函数，则有：

容易证明TN，τ（x）是关于x的凸函数。

类似的可以证明，当j＝1，…，τ－1时，TN，j（x）仍是关于x的凸函数。

接下来证明在两个相邻的应急周期处，Ti，j（x）仍是凸函数。

设在第i＋1个应急周期内，Ti＋1，j（x）是关于x的凸函数，则首先证明Ti，m（x）是关于x的凸函数

容易证明即Ji，m（x，z，v）是关于x的凸函数。因此，当z、v取最优值时，Ti，m（x，z，v）是关于x的凸函数。

类似前述的证明方法，容易证明第（i，j）个应急阶段内仍为x的凸函数，即T″i，j（x）≥0。

三、定理2的证明

当x＋z＋v≥0时，由（6－11）进一步求Ji，j（x，z，v）关于z和v的二阶偏导和联合偏导：

当x＋z＋v＋U＜0时，亦可得到（6－33）式的结论。

由（6－33）式可得第（i，j）个阶段至应急结束的应急期望总成本的海塞矩阵：

因此，第（i，j）个阶段期初运作系统的最优决策组合受一阶条件的符号决定。

而由（6－11）至（6－13）的一阶条件可知的最优取值为0或di或 di＋Δ；而的最优取值为0或V。

四、定理3的证明

证明：采用逆向归纳法证明。本处证明仅考虑应急阶段期初计划投入能力水平大于零时的情况，阶段期初投入能力水平小于零时的证明类似。

首先证明最后一个阶段的应急期望成本是关于x的凸函数。由于最后一个阶段系统自身能力已经恢复到Znormal，则（N，m）个阶段结束时，运作系统不发出正常和快速采购的订单。

则TN，m（x）关于x的一阶偏导

进一步求TN，m（x）关于x的二阶偏导

因此，第（N，m）个阶段的应急运作成本是x的凸函数。

当j＝τ＋1，…，m时，假设TN，j＋1（x）是关于x的凸函数，然后证明TN，j（x）是关于x的凸函数，由于正常订单已经到达运作系统，所以此后阶段内无uN。因此，折现的总期望成本，如下：

求（6－37）式JN，j（x，z，v）关于x的一阶和二阶偏导数：

由于TN，j＋1（x）关于x为凸函数的假设，则T″N，j＋1（·）≥0，又f（·）≥0，则由（6－39）式可得因此，当z，v取最优值时，T″N，j（x）≥0，从而可得TN，j（x）是关于x的凸函数。

接着证明j＝τ时，TN，τ（x）是关于x的凸函数，由于前述的证明可知，TN，τ＋1（x）是凸函数，则有：

容易证明TN，τ（x）是关于x的凸函数。

类似的可以证明，当j＝1，…，τ－1时，TN，j（x）仍是关于x的凸函数。

接下来证明在两个相邻的应急周期处，Ti，j（x）仍是凸函数。

设i＋1个应急周期内，Ti＋1，j（x）是关于x的凸函数，则首先证明Ti，m（x）是关于x的凸函数。求Ji，m（x，z）关于x的二阶偏导：

由（6－41）式可得因此，当z取最优值时，Ti，m（x）是关于x的凸函数。

同理可以证明，Ti，j（x）也是关于x的凸函数。

类似前述的证明方法，容易证明第（i，j）个应急阶段内Ti，j（x）仍为x的凸函数，即T″i，j（x）≥0。

类似的可以证明当x＋z＋v＋U＜0时，Ti，j（x）仍是x的凸函数。

五、定理4的证明

当x＋z＋v≥0，进一步求（6－19）和（6－20）中Ji，j（x，z）关于z的二阶偏导：

由定理3的结论和分布函数非负的假设，从（6－42）和（6－43）式可以看出因此，Ji，j（x，z）是z的凸函数。

同理可证明x＋z＋v＋U＜0时，Ji，j（x，z）也是关于z的凸函数。

因此，该动态模型存在唯一最优的序列，使得多阶段的应急期望总成本最小。其中的取值是一阶条件（6－19）至（6－22）为零时的解。而由于每个周期末内部所恢复能力的投入以及每个周期的第τ个阶段正常供应能力到达运作系统，并且进一步考虑运作系统自身能力的上限约束，因此，最优的序列满足：

而采用“Order－Up－To”的策略，满足如下结论：