第四章　运作系统的能力应急管理模型

第一节　引言

很多大型的工业生产和服务设施，如电力、石油化工、交通运输以及通信等企业的运作是强烈依赖于其运作系统的运作能力，并将系统能力视为企业生存、发展和获取竞争优势的重要来源。一旦突发事件对这些运作系统的能力产生冲击并造成破坏，不仅会给企业的正常运营带来高额的应急成本，甚至对其他行业和社会经济活动地正常运营都会产生巨大的影响。例如，2008年春节期间中国南方13省市遭遇50年不遇的冰雪天气，国家电网和南方电网严重受损造成大范围的电网瘫痪，并由此导致工业生产停滞、交通受阻以及通信设施损毁等一系列次生灾害，整个社会经济遭受巨大损失。

2006年台湾海峡的地震导致中国大陆至港澳台和欧美等方向的通信线路大量中断、互联网大面积瘫痪，中国电信和中国网通的国际语音和专线业务受到严重中断、Internet访问质量严重受损。在应急期间，中国电信除集中力量修复海底通信光缆之外，还租用了通信卫星并同其他电信运营商联系建立迂回路由从而获得临时的通信能力来进行突发事件后的应急。日本丰田企业以及美国西南航空在突发事件后也采取了类似的应急措施，从外部同类型企业处获得临时的生产运营能力。

一些学者，如Clausen、Yu Gang、Kleindorfer、Christopher Tang以及于辉、许明辉等对国内外一些知名企业应急管理的研究和总结表明：当运作系统的一些关键性资源受到冲击时，如参与运作的操作员工、运营设备以及能够提供给顾客的产品和服务的不足（也即运作系统的人、机、物的缺乏），企业决策者需要考虑的是，针对现有运作能力的持有水平，一方面尽快恢复运作系统的内部能力，另一方面从外部能够提供替代能力的企业处临时获取能力来弥补应急期间能力的缺口，以便减小突发事件给运作系统可能带来更为严重的影响。

中国电信在台湾地震后的应急措施表明：应急期间，受害企业不得不面对运作系统内外两个环境的因素。从内部环境来看，对于上述提及的大型运作系统而言，一方面这些系统的能力恢复代价高昂，如购置新的生产设备或服务部件；另一方面受损能力的恢复受到维修部门技术水平、维修部件可得性的影响，使单个时期内的能力恢复数量受限，使得能力的应急呈现多阶段特点。从外部环境看，外部企业能够供给的能力数量并不是无限的，而是存在一个最大的能力供给上限，并且由于外部企业自身的能力需求也会导致外部能力供给数量的不确定性，而外界能力供给数量的不确定性因素直接会影响内部能力恢复数量的决策。因此，基于外部能力供给的不确定性以及内部能力恢复的不经济性和多阶段性等特点，如何进行有效的能力管理从而降低应急期间的成本是管理者需要权衡的。

本章研究内容围绕上述背景，从能力受损的运作系统出发，综合考虑了应急期间企业内部的运作成本和能力缺损可能引致的社会成本，分别针对服务和生产型运作系统能力不同的表现形式，以应急成本最小为目标，首先构建了单阶段运作系统的能力采购和能力恢复模型，然后进一步将模型扩展至多阶段的情况使模型更贴近应急的现实情况，最后采用Hooke－Jeeves算法对模型进行求解，并进行了相应的算例分析。

第二节　基本模型描述

针对突发事件发生后运作系统自身能力的持有水平以及外部可替代能力的供给水平，决策者的目标是在给定的应急期间内使运作系统能力的服务水平尽可能满足外界需求，并使得总应急成本最小。基于企业实际的应急措施，决策者需要从系统内外两个环境出发：一方面从外界可提供替代能力的供应商^[1]处临时获得能力，以弥补当期能力的不足；另一方面让内部能力恢复部门对已损坏的能力进行恢复直至正常投产水平。具体应急模式如图4－1所示。其中，与服务型运作系统能力相比，应急期间生产型运作系统能力可通过实物产品的库存进行缓冲。

图4－1　应急期间运作系统能力的采购和恢复模式

针对上述情况，本章作出如下合理假设。

假设1：运作系统在遭受突发事件冲击之后，运作能力遭到严重破坏并降低到不能正常满足外界对系统能力的需求。除却自身能力不能够达到正常运营水平将会导致的能力缺货成本之外，运作系统还需承担因能力不足导致的社会成本^[2]。

假设2：由于外部能力供应商能够提供支援的能力数量并不是无限的，而是存在一个最大的数量上限。同时，外部能力供应商可提供的能力数量因其客户的需求变化而存在不确定性，因此，外部能力供应商实际能够供应的能力数量存在不确定因素^[3]。

假设3：假设内部能力恢复部门提供的能力恢复数量可控，但一定时期内，系统能力恢复数量的上限受维修部门能力，如维修人员技术水平、维修备件供应以及维修后设备的调试工作等因素的限制，使得能力恢复需要经历多个阶段。

假设4：当期未被满足的需求不会累积到下一阶段，即不存在能力的“Back－Log”现象^[4]。

假设5：运作系统面临的外界需求服从一个概率分布函数^[5]。外界需求通过运作系统的产出来得到满足，并且一单位运营能力转化成一单位的产出。外界需求在一个阶段的末期得到满足。

针对上述假设，以下给出本章模型构建中的符号约定。

突发事件对运作系统能力造成冲击后，运作系统剩余d0个能力。

一个阶段内，外部能力供应商可提供的替代能力数量为xn，xn为［0，S］区间分布的一个随机变量，密度函数为g（xn），累积密度函数为G （xn）。

一个阶段末期，外界对运作系统能力的需求数量为yn，yn为一随机变量，分布密度函数为f（yn），累积密度函数为F（yn）。

一个阶段内，维修恢复部门能够恢复能力数量为rn，rn∈［0，R］，且恢复的能力在阶段末期能够满足外界需求。恢复能力需要投入的恢复成本为P（rn），且能力恢复成本规模不经济，即P′（·）≥0，P″（·）≥0。

每个阶段期初，运作系统决策外购能力的数量为un，该阶段末期系统实际得到的能力数量为min（un，xn），即实际外购能力数量受外部能力供应数量不确定性的影响。

单位能力的缺货成本为k。

单位能力的库存成本为h，对于服务型运作系统而言，h＝0。

自身单位能力的使用成本为c0。

外购能力的单位使用成本为c1。

第n个阶段初期，运作系统持有的能力水平为dn。

运作系统持有能力水平dn＋rn未达到正常投产能力水平Znormal时，运作系统需要为其不足的能力，支付一个社会惩罚成本ω（Znormal－dnrn），其中，ω＞＞k。

首先考虑运作系统正常运行时，为使运作成本最小化需要投入运作能力水平是多少？假设运作系统未受到冲击时，运作系统需要投入的能力水平为Z，则单阶段内系统运作的期望成本为：

容易求得，未受冲击时，单阶段内运作系统投入运营的能力水平的解满足“报童模型”。我们很容易能够求解得到此时最优的投入能力水平为：

很显然，应该认为当系统发生冲击且能力受损后，应急结束时的目标能力水平应使得系统持有的能力恢复到未发生冲击前的最优投入能力水平Znormal。本文将Znormal视为运作系统在正常情况下的能力投产水平。

本章针对服务型和生产型运作系统能力体现方式的不同，分别构建相应的事后能力应急采购和恢复的基本模型，并进行理论推导和证明。

第三节　服务型运作系统应急期间的能力采购和恢复模型

一、单阶段的能力应急采购和恢复模型

对于服务型运作系统（如航空运输，或者产品实效性很强的运作系统，如电力、通讯），应急期间的外购能力是无法贮存到下个阶段，当期多余的运作能力不能用于应对下一阶段的外界需求。

设Zn为第n个阶段期初系统计划投入的运作能力水平，即Zn为运作系统计划用于满足外部需求所应投入的能力数量。第n个阶段期初运作系统持有的能力水平为dn，且dn≤Znormal。考虑到大型运作系统能力缺失将会造成社会损失，系统将为缺失的能力付出额外的惩罚成本ω （Znormal－dn－rn）。由于外界对运作系统能力的需求存在不确定的情况，运作系统在期初持有的能力水平dn存在能够满足期初系统计划投入的运作能力水平，因此，需要确定当Zn≥dn和Zn＜dn两种情况下的运作成本函数。为公式表达清晰简便，推导过程中省略了下标n。

情况1：若Z≥d，即系统持有能力小于计划投入的能力水平，则需要通过外购能力和内部恢复能力来满足需求。此时，该阶段运作系统应急的运作成本为：

情况2：若Z＜d，即系统持有能力大于计划投入的能力水平，则不需要外购能力，即u＝0，但由于d≤Znormal，此时仍需要决策内部恢复的能力数量。此时，该阶段运作系统应急的运作成本为：

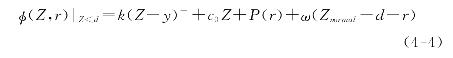
对于情况1而言，运作系统在阶段末外购得到的能力受外部能力供应商实际供给的能力数量限制，还存在u≥x和u＜x两种状况，因此，该情况下运作系统单阶段应急的期望运作成本为：

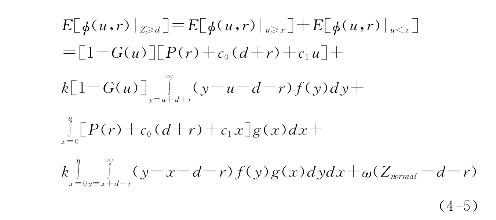
对于情况2而言，运作系统单阶段应急的期望运作成本为：

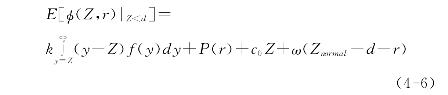
为求单阶段应急期望运作成本存在的最优解，我们需要证明应急期望的运作成本函数是关于（u，r）的凸函数（或拟凸函数）。首先求（4－5）和（4－6）关于（u，r）的一阶条件。

（A）当Z≥d时，求E［φ（u，r）｜Z≥d］关于（u，r）的一阶条件，如下：

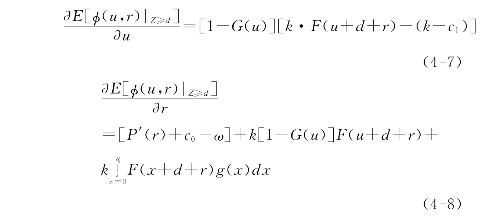
（B）当Z＜d时，求E［φ（Z，r）｜Z＜d］关于r的一阶条件，如下：

定理1：当外部能力供给和内部能力恢复无上限约束时，服务型运作系统为使单阶段应急成本最优，期初计划投入的能力水平存在两个与外部能力供给分布无关的最优值Z1和Znormal，且Z1和Znormal仅由外界能力需求分布函数决定并满足“报童模型”解的形式，即：

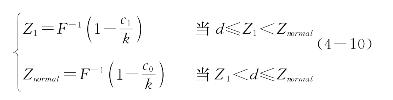
定理2：当外界能力供给和内部能力恢复无上限约束时，服务型运作系统单阶段应急成本最优的（u＊，r＊）组合由两个计划投入最优的能力水平Z1、Znormal（其中Z1＜Znormal）以及该阶段期初运作系统持有的能力水平d决定，且单阶段应急成本最优目标下的应急结束状态由能力缺口（Znormal－d）的边际恢复成本，即P′（Znormal－d）决定。具体结论如下：

（1）d≤Z1时，E［φ（u，r）｜Z≥d］是关于（u，r）的拟凸函数，（u＊，r＊）的决策组合是使计划投入的能力水平达到Z1，且（u＊，r＊）满足如下条件：

（2）Z1＜d≤Znormal时，u＊＝0，r＊由能力缺口（Znormal－d）的边际恢复成本，即P′（Znormal－d）决定，且有如下结果：

进一步考虑外部能力供应商供应的能力数量和内部能力恢复数量存在上限约束的情况，本文得到以下结论。

定理3：外部能力供给和内部能力恢复存在上限约束，即x∈［0，S］，r∈［0，R］时，单阶段应急成本最优的）组合仍由两个计划投入最优的能力水平Z1和Znormal（其中Z1＜Znormal）、期初运作系统持有的能力水平d决定以及S和R决定，且单阶段应急成本最优目标下的应急结束时运作系统持有的能力水平由能力缺口（Znormal－d）的边际恢复成本P′（Znormal －d）和R决定。具体结论如下：

（1）d≤Z1时满足：

其中（u＊，r＊）为（4－11）式的解。

（2）Z1＜d≤Znormal时，－u＊＝0，－r＊的决策存在两种情况：

定理1、定理2和定理3的详细证明见本章附录。

由定理1、定理2和定理3，可以得到如下结论。

第一，服务型运作系统单阶段应急成本最优时，当期最优的期初计划投入水平Z1和Znormal仅与外界对系统能力需求的分布函数相关，且最优的计划投入水平可以方便地由“报童模型”的解给出，极大地方便了运作系统单阶段应急管理的决策。

第二，本文称Z1为能力应急下限水平。当服务型运作系统期初持有的能力水平d≤Z1时，运作系统采用“Order－Up－To”的决策使得该阶段末计划投入的能力水平达到Z1。

第三，当服务型运作系统期初持有的能力水平d∈（Z1，Znormal）时，运作系统考虑应急状态结束时的最优能力恢复根据能力缺口的边际恢复成本P′（Znormal－d）进行决策，要么采取“Order－Up－To”的策略使得运作系统能力达到Znormal，要么使得运作系统的能力水平为d。

结论3进一步验证了Tomlin（2006）发表在Management Science上的研究结果：单阶段应急成本最优的行为，将使得运作系统仅从自身利益最大化的角度来进行能力恢复的决策，且只有当能力缺口的边际恢复成本小于运作系统支付社会惩罚的边际成本时，运作系统才有动力将自身运作能力恢复至正常投产的能力水平；反之，运作系统宁可接受社会惩罚成本也不会去恢复自身的能力水平。

二、多阶段的能力应急采购和恢复模型

对于服务型运作系统，应急期间富余的能力是无法贮存到下个阶段的，下阶段外界对能力的需求仅与下阶段运作系统能够提供的运作能力相关，因而对于服务型运作系统而言并无直观的状态转移方程。因此，对于服务型运作系统而言，上一部分中提到的单阶段的能力应急采购和恢复策略必为最优的策略。

第四节　生产型运作系统应急期间的能力采购和恢复模型

一、单阶段的能力应急采购和恢复模型

对于生产型运作系统（如石化工业和电子工业）而言，其相对于服务型运作系统（如交通运输）或者产品实效性很强的运作系统（如电力、通讯）能力的最大特点是生产型运作系统的能力最终可以表现为满足市场客户需求的实物产品，如电子芯片或石化产品，并可将本阶段富余的能力通过实物产品形式进行库存，用于满足下一阶段的外界需求。

设In为第n个阶段期初的实物产品库存水平。

类似服务型运作系统单阶段的应急成本函数，需要讨论Z＜dn≤Znormal和Znormal≥Zn≥dn两种情况。

可以发现与服务型运作系统单阶段的期望应急运作成本相比，生产型运作系统仅仅在期初计划投入的能力水平分界线上多了一个期初库存I以及h（Z－y）＋两项。为推导的方便和表达的简洁，本章省略了下标n。

情况1：若Znormal≥Z≥d，则系统需要外购能力、内部能力的恢复以及该阶段期初的实物产品库存来满足市场对能力的需求，此时，生产型运作系统单阶段的期望应急运作成本为：

情况2：若Z＜d≤Znormal，则系统不需要外购能力和期初实物产品库存，此时u＝0，I＝0，但由于d≤Znormal，此时仍需要决策内部恢复能力的数量。此时，生产型运作系统单阶段的期望应急运作成本为：

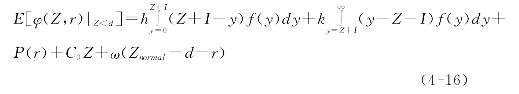
（1）当Znormal≥Z≥d时，由（4－15）式可得生产型运作系统单阶段应急运作期望成本关于u，r的一阶偏导：

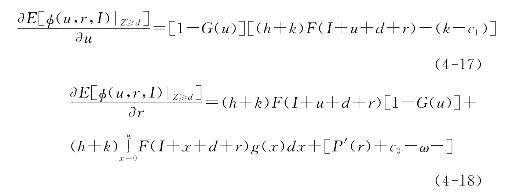
（2）当Z＜d≤Znormal时，此时不需要外界能力支持u＊＝0，但系统内部仍然需要恢复能力，由（4－16）式求得一阶条件：

定理4：当能力可转化成实物进行库存时，生产型运作系统为使单阶段应急成本最优，期初计划投入的能力水平仍存在两个最优值Z1和Z2仅由外界能力需求分布函数决定并满足“报童模型”解的形式。相对于恢复至正常投产的能力水平，生产型运作系统更倾向于利用实物产品库存来进行应急，即：

定理5：当能力可转化成实物产品进行库存且外界能力供给和内部恢复能力水平存在约束，即x∈［0，S］，r∈［0，R］时，使生产型运作系统单阶段应急成本最优的组合由Z1、Znormal、d和I决定，应急结束时生产型运作系统持有的能力水平由能力缺口（Znormal－d）的边际恢复成本P′（Znormal－d）和R决定。具体结论如下：

（1）当d≤Z1时，E［φ（u，r）｜Z≥d］是关于（u，r）的拟凸函数的最优组合是使期初计划投入的能力水平满足Z1，且满足如下条件：

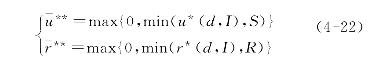
其中u＊（d，I）和r＊（d，I）是一阶条件（4－17）和（4－18）为零时的解。

（2）当Z1＜d≤Znormal时，－u＊＊＝0，－r＊＊的决策仅由能力缺口（Znormald）的边际恢复成本，即P′（Znormal－d）决定，且存在两种情况：

定理4和定理5的证明类似于定理1和定理3的证明，故略。

由定理4和定理5可以看出，生产型运作系统单阶段应急策略类似于服务型运作系统的单阶段应急策略。但相对于服务型运作系统，生产型运作系统的单阶段期初计划投入的最优能力水平会因为实物产品的库存影响而降低，也即相对于服务型运作系统而言，生产型运作系统若仅从单阶段应急成本最优考虑，其能力恢复至正常投产水平的动机将会更小。

二、多阶段的能力应急采购和恢复模型

正如前一节所述，服务型和生产型运作系统其能力表现存在不同的特点，尤其是服务运作系统当期富足的能力无法满足下几个阶段的外部需求，而对于生产运作系统来说，当期富足的能力可通过生产更多的实物产品并进行库存用于以后多个阶段可能面临无法满足外部需求的情况，从而减少相应的缺货风险。

因此，对于生产型的企业而言，当期富余的能力可以通过转化成实物产品的形式进行库存，以防止以后多个阶段内能力不足导致高额的缺货损失。因此，第四章第二节第三部分中的单阶段能力应急采购和恢复策略并不一定是最优的决策。

本部分内容基于生产型运作系统的能力特点，将期末剩余的实物库存能够满足下一阶段外界的需求考虑在内，从而对生产型运作系统多阶段能力（可体现为实物）的应急采购和恢复决策进行推导。

设运作系统能力应急经历0，1，2，…，N－1，N个阶段。

设In为第n阶段期初运作系统拥有的实物库存数量（为推导过程方便，且不失一般性，假设单位能力只能转化为单位实物产品）。则可以得到第n＋1阶段期初的实物库存数量：

当Zn＜dn时，是不需要外界供给能力的，此时的状态转移方程为：

当Zn≥dn时，是需要外界采购能力的，此时的状态转移方程为：

进一步假设若系统提供的能力小于市场需求时，且不允许Back－log现象，此时第n＋1阶段期初的实物库存数量为：

（4－26）式为生产型运作系统能力表现形式的状态转移方程，状态的结束标志是运作系统持有的能力水平恢复至正常投入的最优能力水平，即dN＝Znormal。

设Tn（In）是从第n个阶段开始到应急结束的（N－n）个阶段应急运作的最优期望总成本，且In是第n个阶段期初系统持有的实物产品库存，且Tn（In）有如下表达式：

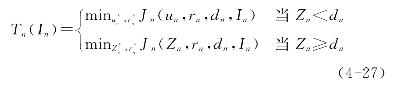
设Jn是期初运作系统状态为dn和In时，在从第n个阶段开始到应急结束的（N－n）个阶段应急运作的期望总成本，则由最优化原理，结合（4－27）式可得Jn的表达式如下：

其中（4－28）式Jn（un，rn，dn，In）中的第2项和第3项是折现后的第n ＋1阶段及以后阶段内应急的总期望成本，分别代表外界能力供给充分和不充分的情况，ρ为折现因子。

当Zn＜dn时，此时系统阶段期初持有的能力水平就能够满足计划投入的能力水平。Jn（Zn，rn，dn，In）关于Zn和rn的一阶偏导为：

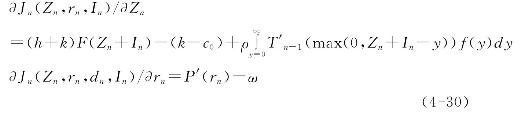
考虑Zn≥dn的情况，此时生产型运作系统需要外购能力以及内部能力恢复来进行能力的应急协调。求Jn（un，rn，dn，In）关于un和rn的一阶偏导为：

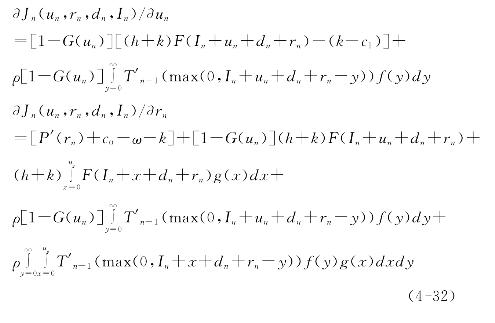
定理6：当第n个阶段期初实物产品库存为In时，从第n个阶段开始到应急结束时的运作系统最优总应急期望成本Tn（In）是一个凸函数，即T″n（In）≥0。

定理6的证明采用逆向归纳法，具体证明参考本章附录。

定理7：生产型运作系统在第n个阶段期初计划投入的最优能力水平受期初产品库存In和能力持有水平dn的影响，并存在两个最优投入能力水平和同样满足“报童模型”解的形式且仅与外界需求函数相关，具体如下：

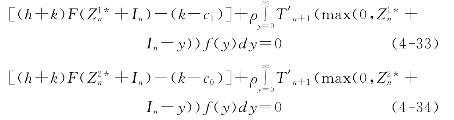
定理8：当外部能力供给和内部能力恢复存在上限约束，即x∈［0， S］，r∈［0，R］时，生产型运作系统多阶段应急成本最优的组合序列由、Znormal、dn和In决定，具体结论如下：

（1）当时，Jn（un，rn，dn，In）关于（un，rn）是一个拟凸函数，满足：(www.daowen.com)

其中是一阶条件（4－31）和（4－32）为零时的解。

（2）当时，运作系统计划投入的能力水平和能力的恢复数量不相关（见（4－29）和（4－30）式）由能力缺口的边际恢复成本P′（Znormal－dn）决定，具体如下：

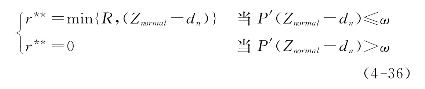
定理7和定理8的证明需要用到定理6的结论，详细证明参考本章附录。

由定理7和定理8的结论并不能看出多阶段内运作系统的应急能力采购和恢复决策序列的相关结果，但定理8给出了当应急时间跨度，即应急所需阶段数给定时，生产型运作系统的能力采购和恢复决策序列存在唯一最优的解序列。

第五节　算例分析

本文设计的多阶段能力应急采购和恢复模型属于随机动态规划问题，模型解的形式并不存在直观的形式，因此，针对本章所研究的事后运作系统的应急运作模型，本章基于Matlab 6．5的开发环境设计了Hooke－Jeeves启发式算法分别对服务型和生产型运作系统应急期间最优的能力采购和恢复决策序列在其解空间进行寻优，并对不同的参数进行了数值仿真和分析。

一、基础数据假设

外界需求Y服从Gamma（α，β）分布，外界需求分布的均值为E［Y］＝1，α＝10、β＝0．1为分布参数^[6]。

外部能力供应商能力供给X在［0，S］上服从均匀分布，外部供应商每个阶段可供给能力数量的上限为S＝0．2。

内部能力恢复成本函数P（r）＝104r2为规模不经济的成本函数^[7]，每个阶段能力恢复数量的上限为R＝0．1。

突发事件发生后，运作系统剩余能力为d0＝0．8。

能力应急的阶段数N＝10。

运作系统单位能力的缺货成本k＝80。

对于生产型运作系统单位能力的库存成本h＝1，对于服务系统而言，由于当期能力无法通过库存形式储存到下一阶段使用，则h＝0。

运作系统自身单位能力的使用成本c0＝2。

外购单位能力的使用成本c1＝3。

未达到正常投产的能力水平，运作系统因能力缺货部分需要支付的社会惩罚成本ω＝800，ω＞＞k。

二、服务型运作系统的能力应急采购和恢复算例分析

根据第四章第二节所列参数，并根据（4－2）式，可以求得运作系统正常运作时，最优的能力投产水平Znormal＝1．7085，根据（4－10）式可以求得应急能力下限水平Z1＝1．6290。

对于服务型运作系统而言，单阶段应急成本最优之和即为应急期间最优的总应急成本，因此，本节内容将分析社会惩罚成本ω以及外部能力供给和内部能力恢复上限［S，R］发生变化时，服务型运作系统最优决策序列和应急成本的变化趋势。

（一）不同社会惩罚成本下服务型运作系统的决策行为

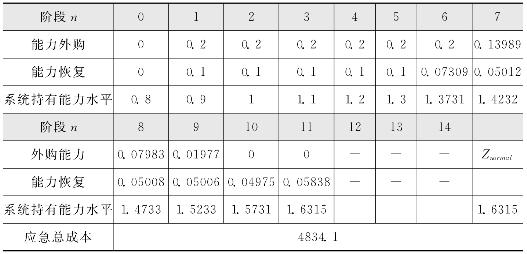
当社会惩罚成本ω取不同值时，服务型运作系统采用单阶段应急成本最优决策时的能力采购和恢复序列的仿真结果，如表4－1至表4－3所示。

表4－1　ω＝800时服务型运作系统的最优决策

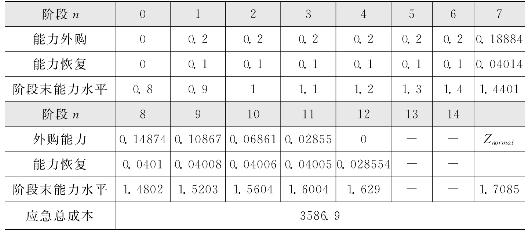
表4－2　ω＝1200时服务型运作系统的最优决策序列

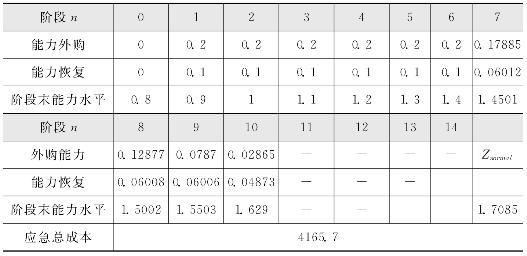
表4－3　ω＝1600时服务型运作系统的最优决策序列

为更清楚地显示当ω取不同值时，服务型运作系统能力应急的最优决策序列如图4－2和图4－3所示。

由表4－1至表4－3以及图4－2至图4－3，可得如下结论。

第一，当能力缺口的边际恢复成本小于社会惩罚成本ω，即P′（Znormal－dn）≤ω时，服务型运作系统才有动机将能力恢复至正常投产的能力水平，否则系统仅将能力恢复至能力应急下限Z1，服务型运作系统宁可承担社会惩罚成本也不会有动机恢复至正常投产的能力水平，如图4－3所示。该结论验证了Tomlin在2005年发表在Management Science上关于应急恢复方面的研究结论。

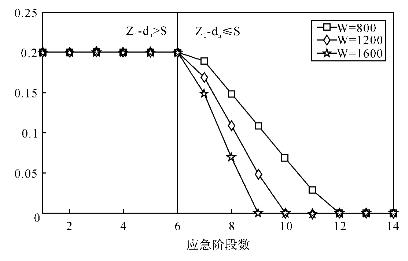
图4－2　ω取不同值时服务型运作系统应急期间－u＊＊n最优决策序列

4－3　ω取不同值时服务型运作系统应急期间－r＊＊n的最优决策序列

第二，ω对应急持续时间和应急成本存在较大影响。ω的增加将使和应急成本有较大幅度的增加，但会使应急持续时间降低，如图4－3和表4－1至表4－3所示。

第三，当期初系统能力缺口（Z1－dn）＞S时，服务型运作系统最优的具有高度的一致性且与ω无关，此时系统倾向于优先使用外部能力，即S，能力恢复决策采用“Order－Up－To”的策略使S＋rn＋dn＝Z1，如表4－1至表4－3以及图4－2至图4－3中第1至第6阶段的决策序列所示。

第四，当期初能力缺口（Z1－dn）≤S时，此后应急期间内，运作系统的内部能力恢复决策具有很高的稳定性，如图4－3第7阶段开始的恢复决策。由表4－1至表4－3可知每阶段能力恢复数量大致满足时的解，使用该决策后的应急总成本仅增加0．1%—1．29%，且ω越大越接近理论上的应急成本^[8]。此时系统只需知道P（r）的函数形式和ω的值即可求得采用“Order－Up－To”的策略，使能力水平达到Z1，即

由上述结论可得以下两方面的管理意义。

从社会的角度来看，对社会影响巨大的公共服务设施，如电站、通信和交通等系统，社会相关部门应对其能力缺货行为采取高额惩罚（如高额的行政惩罚），从而促使这类服务型运作系统缩短企业能力应急时间。这也是为什么相关部门对关系社会经济运行稳定的企业进行高额的行政惩罚的原因，例如，国家电网总公司曾对上海电力徐家汇停电数小时进行了超过900万元的处罚。而从本文模型的仿真结果来看，这样的处罚可以迫使管理者缩短能力修复时间。

从服务型运作系统的角度来看，应急期间的总运作成本受社会惩罚成本ω影响巨大。但从后两条结论来看，应急期间服务运作系统能力的恢复和采购决策却可以得到极大地简化，即知道当期的系统能力缺口数量、外部能力供给的最大值、外部社会惩罚成本以及能力恢复函数即可采用“Order－Up－To”的策略进行应急管理的决策而不需要大量复杂的优化计算。

（二）变化时服务型运作系统的应急总成本分析

当外部能力供应商可提供的最大支援能力上限S和内部能力恢复的上限R取不同值时，服务型运作系统的决策行为会发生如何变化。本部分根据ω＝1200和ω＝1600，分别对应服务型运作系统应急结束时没有动机和有动机恢复至正常投产的能力水平。表4－4和表4－5给出了［S，R］不同组合下所需的应急阶段数以及总应急成本。

表4－4　ω＝1200时服务型运作系统应急持续时间和总应急成本

表4－5　ω＝1600时服务型运作系统应急持续时间和总应急成本

为更清楚地显示当ω取不同值时，服务型运作系统能力应急持续的阶段数以及成本变化趋势，由表4－4和表4－5中数据画出图4－4和图4－5。

图4－4　ω＝1200时服务型运作系统应急持续时间和总应急成本

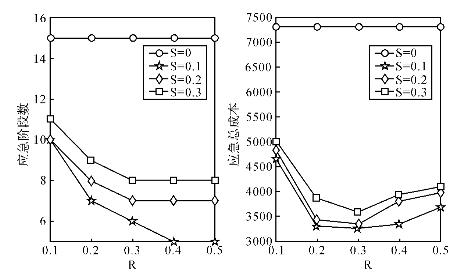
图4－5　ω＝1600时服务型运作系统应急持续时间和总应急成本

由表4－4和表4－5以及图4－4和图4－5，可得如下结论。

第一，服务型运作系统内部能力恢复上限R值越大，系统所需应急时间将减小。但外部能力供应商可提供支援能力的上限S值越大，管理者更加倾向于使用外部供应的能力数量，反而降低了内部能力恢复的动机，使得运作系统应急持续的时间和应急总成本反而增加。但当S＝0时，应急成本剧增且不随R发生任何变化。

第二，服务型运作系统内部能力的恢复上限R值并非越大越好，R值存在一个最优值使得应急总成本最小，见图4－4和图4－5。

为进一步解释上述现象，图4－6和图4－7对ω＝1200和ω＝1600时应急总成本进行了分解，给出了构成应急总成本的两大主要成本，即系统能力的恢复成本和外部惩罚成本。可以明显看出：系统能力的恢复成本和外部惩罚成本呈明显的“效益悖反”现象。当R增加时，每个阶段能力恢复的数量也大为提高，应急所需的时间将会缩短，但系统能力恢复的代价呈上升趋势（来源于能力恢复成本不经济的假设），然而由此带来的好处是因能力缺口所需支付的外部惩罚却大大下降。因此，R的取值并非越大越好，而是存在一个最优值。

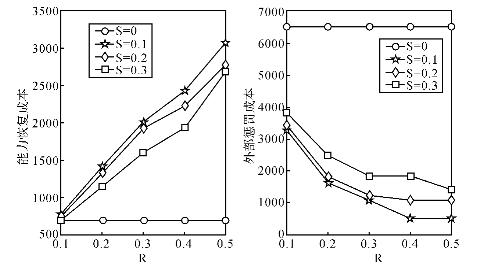
图4－6　ω＝1200时服务型运作系统应急成本分解图

由上述结论可得如下管理学的意义。

高额的社会惩罚将迫使服务运作系统缩短应急持续时间。从该角度来看，对于一些重要的公共服务设施，如电网、通信等运作系统，上级主管部门采取高额的行政处罚是完全有必要的。而现实中我们亦能找到相关案例，如2007年因操作失误导致徐家汇地区停电一小时，为此上海电力向上级主管部门支付了超过900万元的罚金。

外部能力的支援能够降低系统的应急成本，但并非支援能力越多越好，越多的能力支援反而会使得管理者依赖外部能力的支援而降低了能力恢复的动机。为减少能力受损后的总体应急成本，类似于电网、通信等系统应更加注重内部维修部门所提供的能力恢复，加强维修部门的技术实力以及加强与维修备件供应商的关系等措施都将有利于降低应急成本。

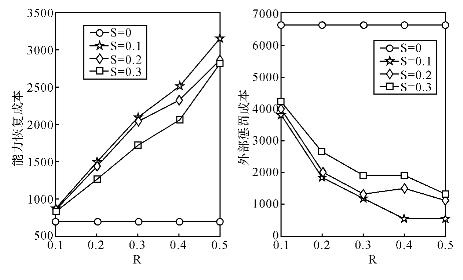
图4－7　ω＝1600时服务型运作系统应急成本分解图

应急期间服务运作系统能力恢复成本和社会惩罚成本出现明显的“效益悖反”现象。在能力恢复成本的非经济性假设下，每个阶段内部能力恢复的数量并不是越大越好，而是存在一个最优值。由此，过分增加维修备件库存，过分强调维修部门的恢复技术投入并不会对应急成本的下降带来必然的贡献。

（三）外部供应能力价格变化时服务型运作系统的应急总成本分析

上述内容是在外部供应商提供能力价格c1＝3情况下的分析结果，那么c1发生变化后，将对服务运作系统的应急总成本造成什么影响？图4－8给出了当c1＝［3，30］时的应急总成本曲线。

图4－8中应急总成本随c1在区间［4801．4，4880．2］之间波动，且无明显规律。进一步计算c1不同取值下应急总成本曲线对应的均值为4832．2，标准差为29．8311，由此几乎可以认为外部能力支援价格的波动对应急总成本几乎没有影响。该仿真结果较为符合现实的应急管理实践：即当能力因突发事件发生缺损之后，管理者通常会积极寻找外部可供支援的能力，而不会考虑该部分能力的价格因素，c1的变化对于整体损失的影响几乎可以忽略不计。从另一个角度来看，本文关于外部高额惩罚（例如，行政惩罚）和能力恢复成本不经济的假设也符合了一些大型公共服务设施能力应急管理的现实。

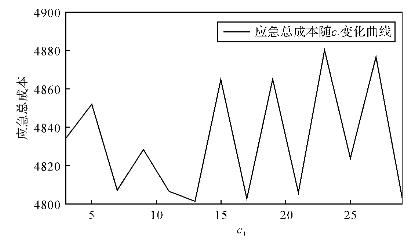
图4－8　c1变化时的服务运作系统应急总成本曲线

由上述仿真可以引出另一个推测：如果企业为能在应急期间获得联盟支援，需要向联盟支付一定的费用（该费用又称联盟租金），租金的不同决定了企业在应急期间可获得的支援或服务在数量上和价格上存在差异。而本章的仿真结果显示：应急期间外部供应商所支援能力数量多少和单位价格高低并不会对应急期间的能力决策造成太大影响，并不会必然降低应急的总成本。从这个角度来看，若仅从应急管理的角度出发，管理者需要考虑在联盟租金和万一突发事件发生之后可从联盟获得的好处之间进行权衡，否则过多支付联盟租金也许得不偿失。

三、生产型运作系统能力应急采购和恢复算例分析

对于生产型运作系统而言，其能力体现于满足外界需求的实物产品，可以通过产品库存来降低应急期间因能力不足带来的高额的缺货损失。根据本章第四节第二部分，本文证明了生产型运作系统在指定的应急期间内，每个阶段外购能力和恢复能力数量的决策存在唯一的解序列。

本章基于Matlab 6．5的开发环境，针对生产型运作系统的能力应急模式设计了Hooke－Jeeves随机动态规划的算法，并对模型进行求解。基于算例，类似服务型运作系统，本文针对社会惩罚成本ω、外部能力供给和内部能力恢复上限［S，R］变化以及应急时间跨度N变化时，分析生产型运作系统决策行为和应急总成本的变化趋势。

（一）不同社会惩罚成本下生产型运作系统的决策行为

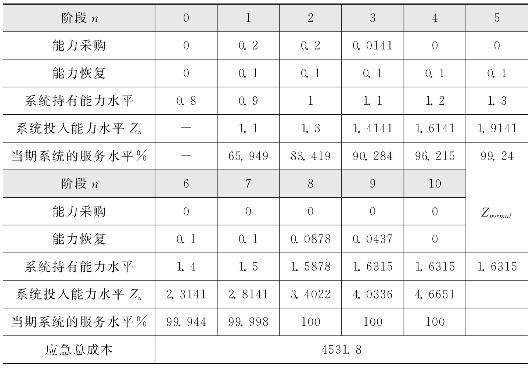
表4－6至表4－8给出了，ω不同取值时，生产型运作系统指定应急时间跨度N＝10个阶段内，以应急成本最小为优化目标时的仿真结果。

可以看出，ω的增加会较大幅度提高应急期间的运作成本。但是ω的变化几乎不会影响生产型运作系统在各个阶段的能力应急采购和恢复及Zn的决策，由表4－6至表4－8同时可以看出，不同ω对应的决策序列仅有0．83%—0．91%的差别，可以认为和Zn的决策序列与ω无关。

上述结论对生产型运作系统事前应急预案的设计具有非常重要的意义，系统可根据外部能力供应商和自身能力恢复部门的情况，事先对可能的系统能力损坏后的应急措施进行详细计划。一旦突发事件爆发，系统可根据事先的应急预案采取相应的能力应急措施，而该措施能够保证在规定的应急时间跨度内，运作系统的应急成本最优。

表4－6　ω＝800时生产型运作系统的最优决策序列及Zn序列和相应的服务水平

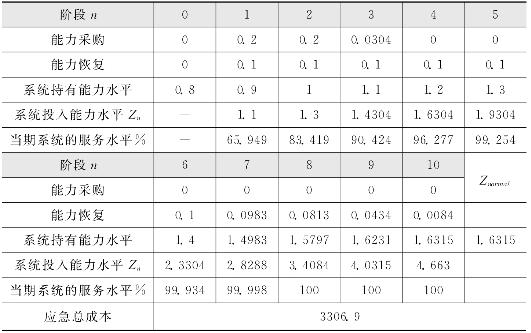
表4－7　ω＝1200时生产型运作系统的最优决策序列及Zn序列和相应的服务水平

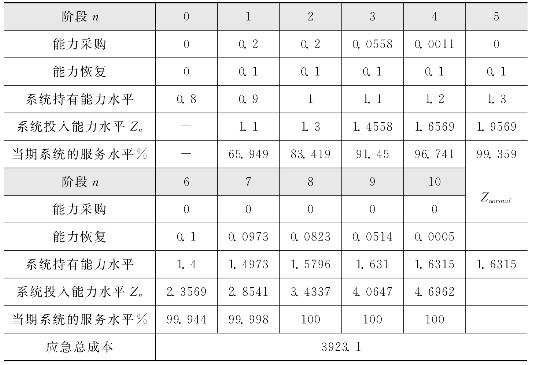
表4－8　ω＝1600时生产型运作系统的最优决策序列及Zn序列和相应的服务水平

（二）S和R变化时生产型运作系统的应急总成本分析

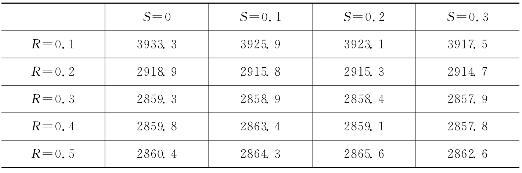
表4－9给出了当不同S和R组合情况下生产型运作系统的应急总成本，其中ω＝1200，N＝10。

可得结论，外部能力供应上限S对运作系统降低应急运作成本贡献很低，仅有0．19%—0．5%的下降幅度；内部能力恢复上限R对运作系统降低应急期间运作成本具有非常重要的贡献，但随着R的增加，应急成本反而增加，主要原因是能力恢复的规模不经济性引起能力恢复成本的增加。上述现象具有重要的管理学意义。

对于生产型运作系统而言，外部能力供应商可提供支援能力数量S越大，系统的应急成本就越低。该结论与服务型运作系统相反，即生产型运作系统更倾向于选择与应急期间可提供更多能力数量的外部能力供应商进行结盟，而其中的一个重要原因，是生产型运作系统的能力可通过实物产品形式进行储存，从而可以降低高额的缺货成本。

与服务型运作系统类似，生产型运作系统内部的能力恢复上限并不是越大越好，而是存在一个最优值。因此，运作系统需要针对外部能力供应商情况，对自身能力的恢复部门进行有效的投资，但过多的投资并不会对应急成本的下降带来必然的贡献。

表4－9　不同S和R组合情况下生产型运作系统的应急成本变化趋势

（三）外部供应能力价格变化时生产型运作系统的应急总成本分析

与服务型运作系统类似，外部供应商提供能力单位价格c1的变化几乎不会对生产型运作系统能力的应急总成本产生影响，不同c1取值下应急总成本曲线对应的均值为3946．5，标准差为14．857如图4－9所示。应急期间，管理者决策的最主要影响因素是外部惩罚成本（例如行政惩罚）和恢复成本不经济。

与服务型运作系统类似，本处的仿真结果同样也表明了应急期间外部供应商所支援能力数量多少和单位价格高低并不会对应急期间的能力决策造成太大影响，并不会必然降低应急的总成本。若管理者仅从突发事件发生之后获得较低价格的能力支援而支付了过多的联盟租金，该行为并不必然降低应急成本。

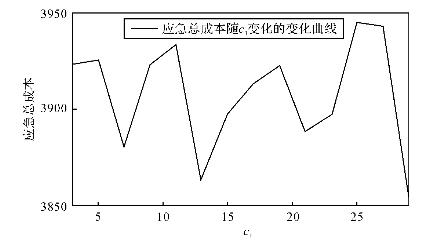
图4－9　c1变化时的生产型运作系统应急总成本曲线

（四）应急时间跨度对生产型运作系统应急总成本的影响分析

当应急时间跨度N变化时，生产型运作系统相应的应急总成本如表4－10所示，其中ω＝1200，S＝0．2，R＝0．1。可以看出，随着应急时间跨度的增加，相应的应急成本会增加，但增加的幅度仅有0．36%—1．38%。导致该现象的原因是：在第9个阶段时，生产运作系统的能力已经得到完全的恢复，不同的N仅仅导致了能力恢复在前9个阶段上出现少许的差异，对应急总成本并没有产生太大的影响，见表4－6至表4－8。上述结论意味着：对于生产型运作系统而言，缩短应急时间对应急成本的下降贡献并不高，管理者应依据突发事件发生后的具体情况决定是否延长或缩短应急时间。

表4－10　生产型运作系统的不同应急时间跨度下的总应急成本

第六节　本章小结

本章针对大型服务设施和工业生产等运作系统因突发事件冲击后能力的损坏进行应急管理，综合考虑了应急期间企业内部的运作成本和能力缺损可能导致高额的社会成本，分别就服务型运作系统和生产型运作系统进行了事后能力应急采购和恢复的模型建立与分析，以应急成本最小化为目标构建了单阶段和多阶段的能力应急模型，最后基于Matlab 6．5的开发环境，设计了Hooke－Jeeves启发式算法对模型的多阶段随机动态规划问题进行了求解，并对结果进行了分析，得到了一些重要的管理学意义。

对于服务型运作系统而言，本章得到如下结论。

第一，从社会的角度来看，对社会影响巨大的运作系统，如电站、通信和交通等系统，社会相关部门应对其能力缺货行为采取高额惩罚（如高额的行政惩罚），可以促使这类服务型运作系统缩短企业能力应急时间。该结论能够较好地反映现实的应急特点，即上级主管部门倾向于通过高额的行政处罚来迫使管理者尽快结束应急状态。例如，2007年上海电力为徐家汇地区电力中断数小时而向上级主管部门支付了超过900万元的罚金。

第二，从服务型运作系统的角度来看，社会惩罚成本和能力恢复成本函数对应急总成本的影响巨大。但由定理1至定理3以及数值仿真可知，应急期间管理者的能力恢复和外购决策可以采用“Order－Up－To”的策略进行分析，从这个角度来看，只要知道当期能力缺口数量、外部能力供给的最大值、社会惩罚成本以及能力恢复函数就可以极大地简化能力应急决策而不需要进行大量的优化计算。从这个角度来看，管理者的应急管理决策会相应地降低难度。

第三，外部能力支援能够降低系统的应急成本，但并不是说外部能力支援数量越多越好。外部能力支援数量越多，会使得管理者更多依赖外部能力支援，反而降低了内部能力恢复的动机，应急所需时间反而增长，而管理者将为此支付更多的外部惩罚成本。由此，相对于外部能力支援的支持，管理者更应该注重自身能力的恢复（但并不是说不需要外部能力支援），内部能力恢复将对应急成本起到重要的影响。这也是航空、地铁、通信、电力（核电站）等大型服务设施十分重视维修部门技术水平的原因。

第四，外部能力支援的价格几乎不会对服务运作系统的应急成本造成影响，若从支付更多的联盟租金以获得更低的能力支援的角度来看，这种行为并不会降低能力受损后系统的总体应急成本。因此，管理者需要明白的是，为了应急而支付的联盟费用很有可能是得不偿失的。

第五，应急期间服务运作系统能力恢复成本和社会惩罚成本呈明显的“效益悖反”现象。在能力恢复成本的非经济性假设下，每个阶段内部能力恢复的数量并不是越大越好，而是存在一个最优值。由此，过分增加维修备件库存，过分强调维修部门的恢复技术投入并不会对应急成本的下降带来必然的贡献。

对于生产型运作系统而言，本章得到如下结论。

第一，社会惩罚成本的变动几乎不会影响生产型运作系统在规定应急时期的最优决策，也即系统最优决策具有非常高的稳定性。这对运作系统制定应急预案具有非常重要的意义，一旦突发事件爆发，运作系统可根据事先的应急预案采取相应的能力应急措施，而该措施能够保证在规定的应急时间跨度内，运作系统的应急成本最优。

第二，应急期间生产型运作系统应更倾向选择可提供最大能力数量的外部供应商作为临时能力的补充。该结论主要是由于生产型运作系统能力可通过实物产品进行储存的特点，而可在应急期间提供最大能力支援的企业显然是可以降低受损系统可能面临高额的能力缺货损失。能力支援的价格对应急总成本机会不会造成影响。因此，从联盟角度来看，管理者更应该考虑的是联盟租金是否能够在应急期间给生产型运作系统带来更多的能力支援（而非能力支援的价格）。

第三，对于生产型运作系统而言，缩短应急时间对应急成本的下降贡献并不高，决策者应依据突发事件发生后的具体情况决定是否延长或缩短应急时间。导致该结论的主要原因是，受损的能力在某一固定的阶段之内已经得到恢复，应急时间的不同仅仅在能力恢复数量的分配上存在少许差异，但该差异导致应急成本的差异几乎可以忽略。

第四，与服务型运作系统类似，系统内部的能力恢复上限并不是越大越好，而是存在一个最优值。因此，运作系统需要针对外部能力供应商情况，对自身能力的恢复部门进行有效的投资，过多的投资（如增加维修备件库存和增强维修技术能力的投入）并不会对应急成本的下降带来必然的贡献。

总结：对于服务型运作系统而言，本文得到5个具有重要管理学意义的结论，对社会管理部门的应急政策制定以及运作系统本身在应急期间的科学决策均具有一定的指导意义。对于生产型运作系统而言，本文得到4个方面管理学的意义，对运作系统预案设计、能力投资、联盟选择以及应急时间跨度的决策均具有一定的指导意义。

【注释】

[1]本文中外部能力供应商指的是具有相同或可提供类似替代能力的企业，例如2007年1月26日，台湾海峡的地震致使中国电信和中国网通六根海底光缆断裂，导致中国大陆至港澳台、欧美的Internet和国际语音业务大量中断。在海底光缆修复过程中，中国电信紧急租用通信卫星并同其他电信运营商联系建立迂回路由从而获取临时的通信能力。因此，通信卫星、其他电信运营商对于中国电信而言即为外部能力供应商。

[2]该假设具有一定的合理性。对于电网、通信设施、炼油厂等大型的运作系统而言，自身能力不能够达到正常运营水平不仅会导致能力缺货成本，而且这类运作系统通常是社会其他生产运营部门的基础性服务和产品的提供商，一旦能力缺损往往会产生更高的社会成本。例如，上海电力曾为其在2007年的徐家汇停电事故向上级主管部门支付了900万元的罚金，而美国第一能源AFE因其北美大停电事故至今仍官司缠身。

[3]例如，通信卫星能够提供通信能力受其设计最大容量限制。

[4]该假设具有一定的合理性。例如，电力、通信等运作系统能力的产出，即电能和通讯具有很强的时效性，当阶段的未被满足需求不会累积到下一阶段。

[5]该假设的引入是为了简化模型的推导过程。实际情况中也存在外界需求分布服从一概率分布函数，例如，某地区的电能、能源的需求在一定时期内围绕某一均值进行上下波动。而对于一些时效性很强的产品和服务，例如，制药、交通、通信等运作系统而言，应急期间外界需求可能会发生较大波动，该假设排除了这种情况。

[6]Gamma分布函数是一个常用的概率分布函数，通过分布参数的选择Gamma分布函数族涵盖了大量的特殊分布函数，如指数分布、Pission分布和Beta分布，因此，运作管理中的大量文献采用Gamma分布函数来描述外界需求的不确定性。为数值仿真的方便计算，本文将外界能力需求的均值进行归一化处理。

[7]该假设具有一定的合理性，因为应急期间决策者需要调动系统内部的维修力量进行维修；另外，对于电力、通信、半导体工业和石化炼油等大型的运作系统，一些运营备件，例如，发电机的转子、大型通信路由设备、半导体封装部件等部件的采购成本和购置提前期均较长，这类设备备件的紧急供应会导致更高的备件采购成本。应急期间需要恢复能力的数量越多，系统付出的恢复代价可能呈现出指数型上升。当然具体的恢复函数可根据不同运作系统的实际情况给出，本文给出的恢复函数仅从方便数值计算的角度进行设计。

[8]采用P′（rn）＝ω决策时，不同ω时应急期间的运作成本：ω＝800，cost＝3587．7，ω＝1200，cost＝4166．2；ω＝1600，cost＝4834．5。