碳纳米管电离型气敏传感器检测机理的实验研究

黄　洁　周　瑶　周于人　尹芳缘　惠国华

（浙江工商大学 食品与生物工程学院，浙江杭州310012）

［摘 要］ 随机共振是某些非线性动力学系统中的普遍现象，它向人们展示了噪声在非线性体系中的积极作用。文章首先通过对多稳动力学系统随机共振的数值模拟研究，得到多重随机共振仿真结果。在研究碳纳米管电场效应实验中，对碳管气敏传感器系统施加电白噪声，改变噪声强度观察到系统产生多重随机共振现象，这与数值模拟研究结果一致，为碳纳米管电离型气敏传感器机理研究提供了一种新的思路，从而将开展长期的研究以探索该类传感器在食品品质检测领域的潜在应用。

［关键词］ 气体电离；气敏传感器；碳纳米管；多稳态随机共振

Experimental Study of Carbon Nanotube Ionizationgas Sensor Sensing Mechanism

Huang Jie Zhou Yao Zhou Yuren Yin Fangyuan Huiguohua

（College of Food Science and Biotechnology，Zhejianggongshang University，Hangzhou Zhejiang 310012，China）

Abstract：Stochastic resonance（SR）is a popular phenomenon in certain non－linear dynamics systems．This phenomenon presents us the positive effects of noise to non－linear systems．In this paper，numerical modeling results of SR in multi stable dynamics system has been investigated．In the study of carbon nanotube electrical field effects，electrical white noise is added into carbon nanotubegas sensor system．The noise intensities have been changed to obtain multi SR．This study provides a novel way to investigate carbon nanotube ionizationgas sensor mechanism．

Key words：gas ionization；gas sensor；carbon nanotube；multi stable stochastic resonance

随机共振已经成为非常活跃的研究领域，在许多场合都得到了验证。在非线性动力学系统中，适当地施加噪声可以提高信噪比。1981年，邦济等人使用随机共振模型解释地球气候的周期性变化，目前这一理论已经在电子、生物、医学等领域广泛应用。

磁化等离子体中系统输出信号的信噪比随噪声的影响出现波动的现象，在1995年就已经有所报道，Lin等人称之为“类随机共振现象”。杨洪波等进行了非磁化等离子体Hopf分岔处的随机共振实验，应用系统内禀的周期驱动力和外加白噪声，观察到在Hopf分岔点附近的随机共振现象，输出信号的周期成分相对于背景噪声的信噪比和外加噪声强度有关。通过一维过阻尼系统随机共振理论预期结果一致。

定向碳纳米管的电离型气敏传感器具有使用方便、响应速度快等优点，本文通过实验观察了该传感器放电过程中的多重随机共振现象，并通过多稳动力学系统随机共振的数值模拟，得到了实验观察结果一致的随机共振曲线。

1．　实验材料和设备

1．1　仪器与试剂

54641A示波器（美国安捷伦公司制造）；POLIPOWER交流电源（丹麦制造）；QJ6005直流稳压电源（苏州市泓成电子科技有限公司制造）；VC890D数字万用表（深圳胜利高电子科技有限公司制造）；自制0—1200V连续可调高压直流电源；自制碳纳米管生长电炉；纯度99．999%的高纯铝板（上海异型材料有限公司生产）；硫酸钴（江苏宜兴化学试剂厂生产）。所用试剂均为分析纯，水为去离子水。

1．2　氧化铝模板上定向碳纳米管的生长

高纯铝板在丙酮、乙醇混合溶液中经超声清洗后，在体积比4∶1的乙醇和高氯酸混合溶液中抛光10min。取出用去离子水洗净后置入0．3mol／L的草酸溶液中，使用直流电压40V阳极氧化1h以后，置于50℃的磷酸和铬酸混合溶液中，去除一次阳极氧化膜，在相同条件下二次氧化20min后，取出在5%的磷酸溶液中50℃扩孔15min，孔的大小、孔间距及深度分别为60nm、100nm和2μm，完成AAO模板的制备。然后使用交流电源于60g／L的硫酸钴与25g／l的硼酸的混合溶液中在AAO模板上电沉积钴颗粒（颗粒大小在60nm左右），将沉积有钴粒子的AAO模板放到电炉中，在电炉温度达到645℃时，通入乙炔气和氢气（流量比为1∶2）生长5—10min，在氮气保护下冷却至室温取出。如此得到了生长在氧化铝模板上的定向碳纳米管。在电镜下观察制备过程。

1．3　实验检测传感器及总体装置

碳纳米管气敏传感器以碳纳米管电极作为阳极，铝板作为阴极，如图19－1所示。在碳纳米管电极上覆盖绝缘薄膜材料，切除应用气体检测部分的薄膜使此部分碳纳米管外露，再将纯铝覆盖在薄膜之上。这样只有碳纳米管电极用于气体检测处的部分和阴极相对，有效地控制了两极间距。如果要改变间距，可以通过使用不同厚度绝缘薄膜的方法来改变距离，使极间距离在几十到几百微米范围之内方便地调节。实验装置见图19－2，碳纳米管气敏传感器密闭在待测气体气室中，通过对电极上电压的连续调节，实现对气体检测电路电晕放电的参数测量，其中R＝100kΩ，R1＝1kΩ。

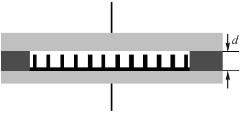
图19－1　碳纳米管电极结构

图19－2　气体放电实验系统

1．4　多稳态系统仿真模型

根据气体放电中的多重随机共振现象，结合动力学系统的多稳态结构特点，使用差分形式进行数值仿真实验：

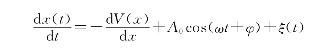
式中：ξ（t）为高斯白噪声，D是噪声强度，Δt为步长，V（x）为势函数。

仿真实验结果表明折线势函数和光滑曲线势函数对随机共振曲线形状、共振峰位置和强度没有影响，只是引起信噪比较小的平移。因此，我们构建了折线势函数，如图19－3所示。

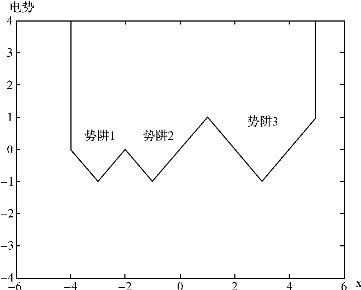
图19－3　折线势函数

2．　结果和讨论

2．1　多稳态共振系统数值模拟结果

多重随机共振模拟结果如图19－4所示，系统的随机共振信噪比曲线出现两次极大值，这与气体放电中的多重随机共振现象相吻合。(www.daowen.com)

在噪声强度较低的区域，质点在势阱1和2之间的在噪声的诱发下产生第一次随机共振，信噪比出现第一个极大值。增大噪声强度，质点从势阱2跃迁势阱3之间的机会增加，但是由于第一次随机共振的运动状态被破坏，因此信噪比迅速下降。此时如果再继续增加噪声强度，质点获得足够的能量在势阱1、2和3之间进行连续运动，信噪比又重新开始上升。当噪声增大到一定强度，使得质点在三个势阱间运动的周期接近驱动力周期时，第二次产生随机共振现象，信噪比出现第二个极大值。模拟结果为气体放电的多重随机共振现象给出了一个合理的解释。

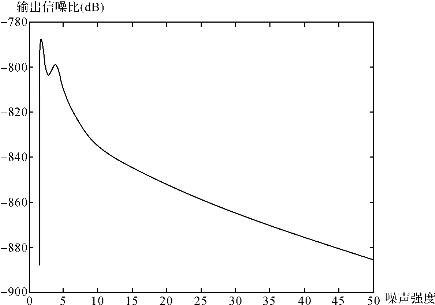
图19－4　多重随机共振模拟仿真

2．2　多稳态共振系统数值模拟结果

图19－5是系统在施加不同强度噪声情况下，以示波器记录气体放电电流信号的傅立叶频谱。在噪声强度为零时，系统的电流变化很小，在频谱中观察到一个1．65MHz左右的周期性成分，如图19－5（a）箭头所示，此时系统信噪比较低。随着噪声强度增加到9．18V时，1．65MHz的周期成分得到明显的增强，信噪比提高，如图19－5（b）所示，此时由于放电电流增强因而出现了零星的放电脉冲。增加噪声强度至12．37V，1．65MHz的周期成分出现明显下降，信噪比迅速减小，如图19－5（c）所示。继续提高噪声强度至15．68V，出现了与普通随机共振不同的现象，1．65MHz的周期成分又得到加强，信噪比出现回升，如图19－5（d）。

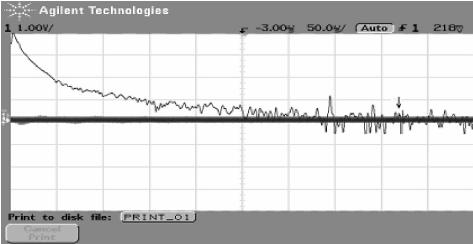
（a）

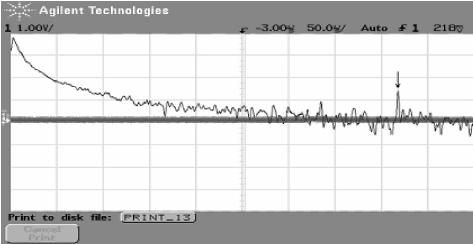
（b）

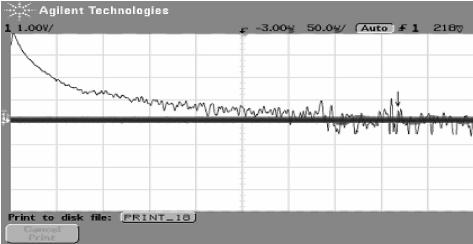
（c）

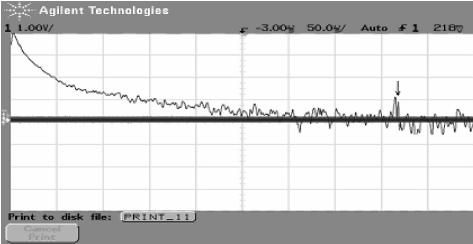
（d）
图19－5 不同噪声强度下的电流扰动频谱图

1．65MHz的周期性成分的产生机理尚不清楚，我们通过对气体放电性质分析给出一种可能的解释。气体放电是非线性科学的重要研究领域，直流放电等离子体在该领域中有着举足轻重的地位。根据气体放电物理理论，自持暗放电区和前辉光放电区域相邻，实验系统处于自持暗放电区，此时可以观察到零星的放电脉冲序列。当加入噪声后实验系统向前辉光放电区域过渡，电极极板间处于一种稳定的非线性直流放电等离子体状态。相对于离子而言等离子体中的电子处于一种非热平衡状态，因此也称为低温等离子体。等离子体中存在高密度的带正电的离子和带负电的电子，处于持续运动状态。电离产生的正负电荷总是成对出现，它们的消失比率也是相等的，因此等离子体从整体上说表现为电中性。如果在等离子体的某一局部区域瞬时出现正或负的空间电荷。等离子体振荡是等离子体中粒子群的相互作用而形成的有组织的集体运动，电子等离子体频率和离子等离子体频率分别表示电子和离子能够响应集体运动的最高频率。

电子和离子的等离子体频率可以用下式来计算：

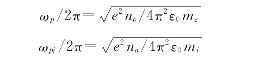
其中，no为等离子体密度，ε0是真空中的介电常数，me是电子的质量，mi是离子的质量。辉光放电中粒子浓度大约在1016 m－3，在相同的振荡条件下，我们考察离子的等离子体振荡频率。氩的离子等离子体频率约为3．3MHz，氮约为1．95MHz，氖约为2．33MHz，氦约为1．04MHz。在传感器系统气体放电中，我们分析可能是因为空气中含有的多种成分在碳纳米管传感器极间等离子体中出现振荡，产生了1．65MHz的周期性成分，还需要进一步的研究证实。

数值模拟采用三势阱折线分段势函数，以两个双稳态随机共振邻接组合去构建多稳态随机共振模型。如果实验观察到更多重随机共振的情况，可以使用相同的方法来构造动力学模型，该方法具有一定的扩展性。气体放电中的多重随机共振研究为气体的检测提供了一种新的思路：在电路中施加适当强度噪声，诱发混合气体中目标成分气体产生随机共振，以频谱中的特征频率，实现气体检测的目的。

3．　结 论

实验观察到外加白噪声诱发碳管气敏传感器系统内部1．65MHz周期性分量产生多重随机共振现象，可认为是由于空气中的多种气体成分在等离子体中产生等离子体振荡因此产生了这个周期性分量。通过对多稳动力学系统随机共振的数值模拟研究，得到的随机共振曲线与实验结果相一致。该数值仿真方法具有一定的扩展性，可以应用到更多重随机共振的情况。

［参考文献］

［1］Douglass JK，Wilkens L，Pantazelou E，et al．Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance［J］．Nature，1993（365）：337－340．

［2］Mc Namara B，Wiesenfeld B，Roy R．Observation of stochastic resonance in a ring laser ［J］．Physical Review Letters，1988，60（25）：2626－2629．

［3］Bulsara AR，Schmerag．Stochastic Resonance inglobally Coupled Nonlinear Oscillators ［J］．Physical Review E，1993，47（5）：3734－3737．

［4］Chapeau－Blondeau F，Godivier X．Theory of stochastic resonance in signal transmission by static nonlinear systems［J］．Physical Review E，1997，55（2）：1478－1495．

［5］Hug，Dechung，Wen X D．Stochastic resonance in a nonlinear system driven by an aperiodic force［J］．Physical Review A，1992，46（6）：3250－3254．

［6］Benzi R，Suters A，Vulpiani A．The mechanism of stochastic resonance［J］．Journal of Physics A，1981（A14）：L453－457．

［7］Lin I，Liu J．Experimental observation of stochastic resonancelike behavior of autonomous motion in weakly ionized rf magnetoplasmas［J］．Physical Review Letters，1995，74（16）：3161－3164．

［8］杨洪波，刘万东，郑坚，等．非磁化等离子体Hopf分岔处随机共振实验［J］．物理学报，2000，49（3）：508－512．

［9］惠国华，吴莉莉，潘敏，等．基于定向碳纳米管气体放电的气敏传感器研究［J］．分析化学，2006，34（12）：1813－1816．

［10］董丽芳．气体放电等离子体动力学［M］．保定：河北大学出版社，1998．

［11］菅井秀郎．等离子体电子工程学［M］．北京：科学出版社．2002．

［12］徐学基，诸定昌．气体放电物理［M］．上海：复旦大学出版社．1995．