第四节　金融风险预警体系构建

从上一节的模型结果中，我们不难发现，虽然MS-VAR模型对每次危机都准确地发出了预警信号，但是每次发出信号的时候，危机其实都已经发生了。从严格意义上讲，那个信号只能是一个报警信号而不是一个预警信号。为了能够起到真正的“预”警作用，本研究试图引入ARIMA模型对外汇危机进行预警。本节首先对ARIMA模型进行简要介绍，然后运用ARIMA模型对汇率、国家外汇储备、国内利率、贷款/存款、实际利率、货币供应量、股票价格指数和房价指数从2010年10月到2011年6月的数据进行预测，然后使用第二节的方法，重新计算货币危机指数、银行危机指数、资产泡沫危机指数，并将其代入MS-VAR模型，观察预测的数据能否使MS-VAR模型发出预警信号。

一、ARIMA模型

在了解ARIMA模型之前，我们先介绍ARMA模型，因为ARIMA模型是在ARMA模型的基础上发展起来的。

（一）ARMA模型

ARMA模型（auto-regressive and moving average model）是研究时间序列的重要方法，是以自回归模型（简称AR模型）与滑动平均模型（简称MA模型）为基础“混合”构成。在市场研究中常用于长期追踪资料的研究。ARMA模型共有三种基本形式：

1.自回归模型（auto-regressive，AR）

如果时间序列y_t满足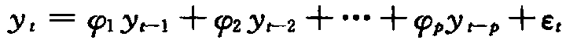，其中ε_t是独立分布的随机变量序列，且满足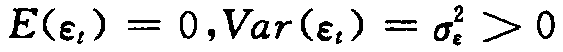，则称时间序列y_t为服从p阶的自回归模型。自回归模型的平稳条件为：滞后算子多项式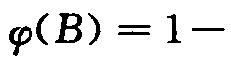

的根均在单位圆外。

2.移动平均模型（moving-average，MA）

如果时间序列y_t满足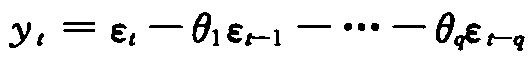，则称时间序列为y_t服从q阶移动平均模型。需要指出的是移动平均模型在任何条件下皆平稳。

3.混合模型（auto-regressivem oving-average，ARMA）

如果时间序列yy_t满足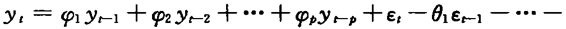

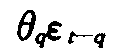，则称时间序列y_t为服从（p，q）阶自回归滑动平均混合模型。当q＝0时，模型即为AR（p）；当p＝0时，模型即为MA（q）。

（二）ARIMA模型

1.ARIMA模型推导

ARMA模型应用十分广泛，但是该模型有一个局限，那就是时间序列必须是平稳的才可以应用ARMA模型。因为大多数经济数据是含有趋势性的、非平稳的，博克思（Box）和詹金斯（Jenkins）将差分方法和ARMA模型结合创造了著名的ARIMA模型。

设y_t是非平稳序列，经过d阶差分后为平稳序列，即y_t是d阶单整序列，即y_t～I（d），令：

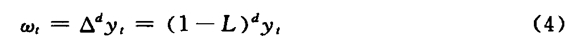
其中L为滞后算子，则ω_t为平稳序列，即ω_t～I（0），于是可以对ω_t建立ARMA（p，q）模型：

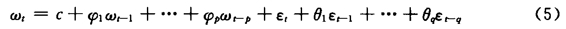
用滞后算子表示为：

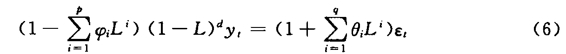
其中L为滞后算子，d ∈Z，d＞0。

如式（6）这样经过d阶差分变换的ARMA（p，q)模型称为ARIMA（p，d，q)模型（autoregressive integrated moving average）。

2.ARIMA模型的应用流程

博克思和詹金斯还提出了针对非平稳时间序列建模具有广泛影响的建模思想，能够对实际建模起到指导作用。博克思和詹金斯的建模思想可以总结为以下六个步骤：

（1）根据时间序列的散点图、自相关函数图和偏自相关函数图识别其平稳性。

（2）对非平稳的时间序列数据进行平稳化处理，直到处理后的自相关函数和偏自相关函数的数值非显著、非零。

（3）根据所识别出来的特征建立相应的时间序列模型。平稳化处理后，若偏自相关函数是截尾的，而自相关函数是拖尾的，则建立AR模型；若偏自相关函数是拖尾的，而自相关函数是截尾的，则建立MA模型；若偏自相关函数和自相关函数均是拖尾的，则序列适合ARMA模型。

（4）参数估计，检验是否具有统计意义。

（5）假设检验，判断（诊断）残差序列是否为白噪音序列。

（6）利用已通过检验的模型进行预测。

3.模型应用与数据预测

（1）序列特征分析。

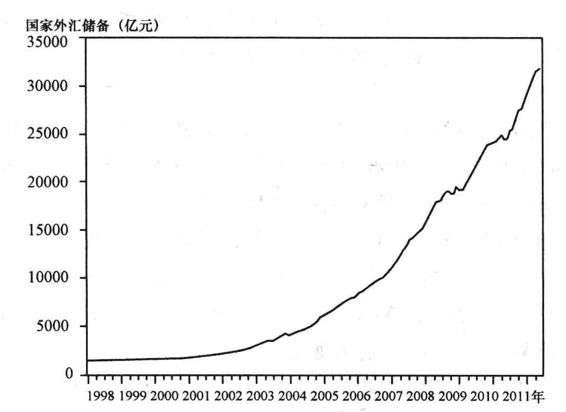
我们先对第一个指标——国家外汇储备（FER）进行预测，使用国家外汇储备（FER） 1998年1月到2008年6月的数据绘制折线图如图9-7。

从图9-7中可以看出，存在明显的时间趋势，而且是不平稳的。通过ADF检验得出的t值为3.15，远大于置信水平1%、5%、10%的临界值，因此可以认为序列FER是非平稳的。

(www.daowen.com)

图9-7　国家外汇储备折线图

为了减少FER的趋势波动，对FER进行一阶自然对数差分才得到序列DFER。绘制DFER的自相关图如图9-8。

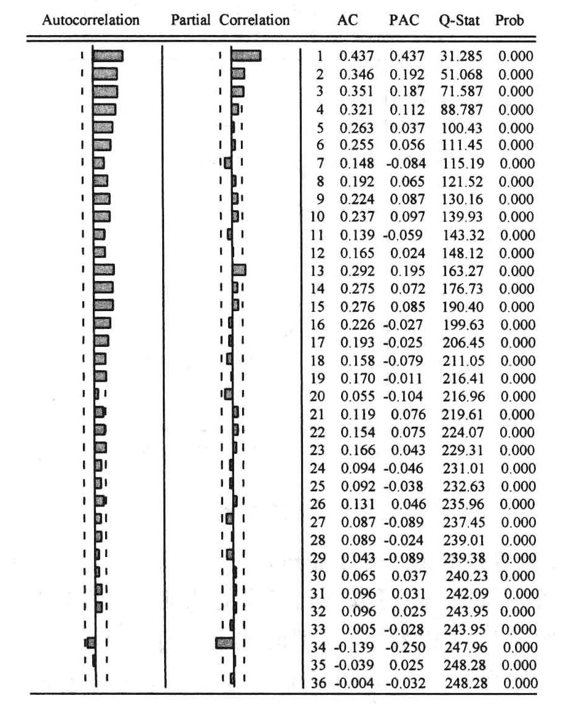
图9-8　DFER自相关图

使用ADF检验得到t值为－7.90，远小于置信水平1%、5%、10%的临界值—3.48、－2.88、－2. 56，因此序列DFER是平稳的。

（2）ARIMA模型建立与应用。

我们将对序列FER建立ARIMA（p，d，q)模型。由于序列FER经过一阶自然对数差分后序列的趋势性被消除，因此d＝1；观察序列DFER的自相关序列图，DFER的自相关函数和偏相关函数都是拖尾的，自相关函数一直到滞后20阶才变得不显著，这表明MA过程应该是低阶的，因此我们设定p值为1。偏相关函数第1、第2阶都比较显著，并且从第3阶开始下降很大，因此我们设定q值为2。综上所述，我们建立ARIMA（1，1，2）模型。通过建立ARIMA（1，1，2）模型，使用EVIEWS7.0运算，结果如下：

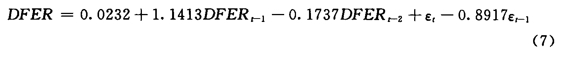
t＝5.7　　　t＝11.30　　t＝－1.90　　　t＝－15.64

p＝0　　　　p＝0　　　　p＝0.0587　　　p＝0

R²＝0.28　　　　DW＝2.00

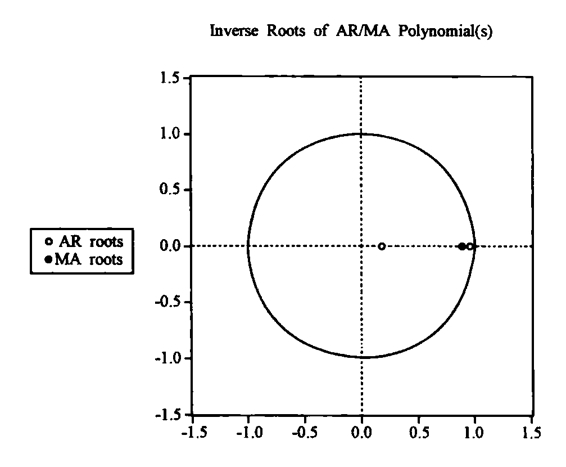
图9-9　特征根倒数图

从式（7）中各系数参数的t统计量和p值可以看出，模型的各参数都在95%的置信区间内显著。从图9-9可以得到模型的特征根的倒数都小于1，该模型是平稳可逆的。由图9-10可以看出，模型的残差不存在序列相关，即模型的残差序列是一个白噪音序列。总之，ARIMA（1，1，2）模型可用来预测2010—2011年的结果。

图9-10　残整序列图

（3）数据预测。

使用ARIMA模型的预测功能。由于数据原因，我们仍然使用2010年10月到2011年6月的国家外汇储备数据进行预测。因为动态法预测下一期的时候会使用上一期的实际数据，这就使得我们的预测跨度只有一个月的时间。为了加长我们的预测时间跨度，本研究选择静态法进行预测。预测结果如图9-11。

将预测的2010年10月到2011年6月的数据和1998年1月到2010年9月的数据放到一起得到包含预测数据的国家外汇储备FOFER（ForecastFER）。

4.多次预测

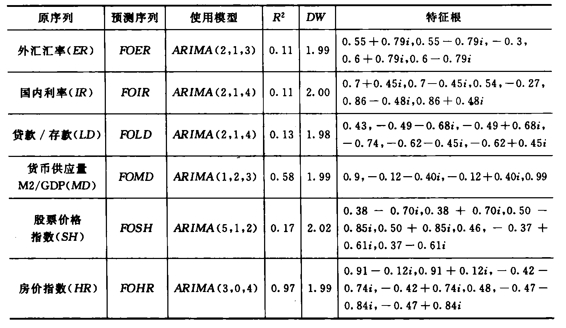
通过重复1～3小节的计量操作，我们可以计算出包含预测数据的外汇汇率（FOER）、实际利率（FOIR）、贷款/存款（FOLD）、货币供应量M2/GDP（FOMD）、股票价格指数（FOSH）和房价指数（FOHR）。鉴于篇幅限制，在此不再赘述，只将各序列预测模型列表如表9-4。

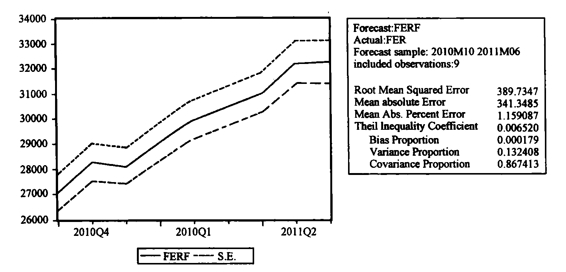
图9-11　预测结果图

表9-4　各序列预测模型列表

二、金融风险预警体系构建

根据上述模型得到的包含预测数据的国家外汇储备（FOFER ）、外汇汇率（FOER）、实际利率（FOIR）、贷款/存款（FOLD）、货币供应量M2/GDP（FOMD）、股票价格指数（FOSH）和房价指数（FOHR），重新利用前述方法计算得到预测的2010年10月到2011年6月的货币危机指数，将预测得出的危机指数和实际的1998年1月到2010年 9月的危机指数放在一起，代入MS（3）-VAR （3）中得到结果如图9-12～图9-14及表9-5。

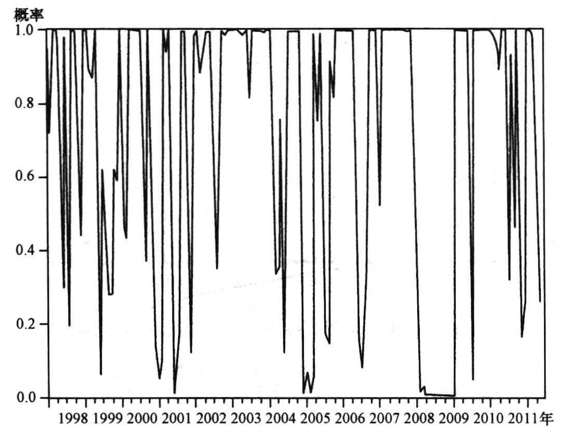
图9-12　预测三个危机指数低风险区平滑移动概率（smooth probabilities of regime 1）

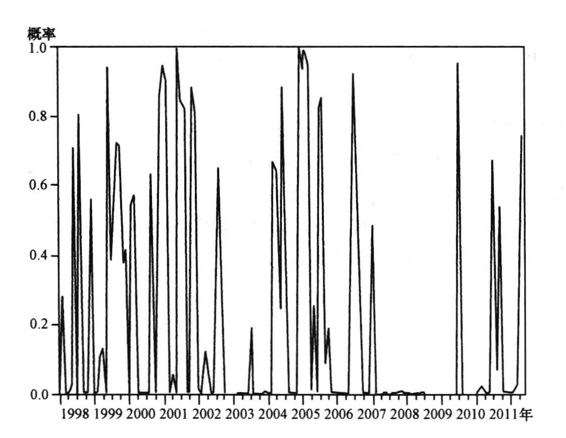
图9-13　预测三个危机指数中风险区平滑移动概率（smooth probabilities of regime 2）

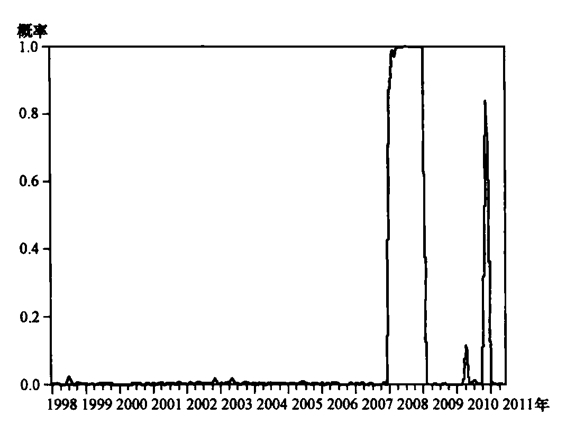
图9-14　预测三个危机指数高风险区平滑移动概率（smoothprobabilitiiesofregime3）

表9-5　区制转移概率矩阵

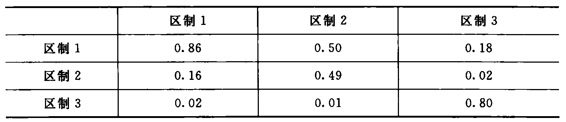
以上图表告诉我们，加入预测数据的MS-VAR模型还是较为准确地对2008年的全球次贷危机发出了高风险警告信号。这表明我们将ARIMA模型和MS-VAR模型结合在一起可以提前约半年时间对危机发出准确预警。

综上所述，本章两大主要结论为：①证明低风险等级、中风险等级和高风险等级的划分方法与我国经济的实际情况比较吻合，而且MS（1）-VAR（3）模型是适合我国国情的预警模型。②将ARIMA模型和MS-VAR模型结合在一起可以提前约半年时间对危机发出准确预警。