第二节　MS-VAR模型

在时间序列模型中，大多数时间资产价格会因某一个可识别的重大事件而发生较大变动。例如在以周为单位的时间序列中，美联储的利率和国债利率是相关联的，但是放在更长的时间段来看，美联储的利率还会受到各种货币财政政策的影响。例如1979年美联储的一次公开市场操作就造成了利率的不连续变化，那么这个时间序列将会被分为两段来进行研究。很多经济上的重大事件都会影响金融的时间序列，例如第二次世界大战和欧佩克突然减少石油供给，这些都应该被认为是金融时间序列中可以识别的一段时期。

假设我们知道所有的金融时间序列数据，但并不知道金融的时间序列被划分为哪几个时期。当遇到不连续的时间序列数据时，我们是否可以推测出时间序列数据已经进入到另一个时期？答案是肯定的。如文献综述中提到的一样，KrolzingH -M（1997）提出马尔科夫区制转换的向量自回归模型（Markov-Switching Vector Autoregress，MS-VAR）成功地解决了这一难题。

MSV-AR可以视为基本有限阶VAR（q）模型的一般化形式。考虑下面这个X维时间序列构成向量y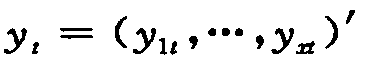t＝（y1t，…y，xt）′的q阶自回归过程：

其中，t＝1，…，T，ut～N（0，1），y0，…，yt－q均为既定值。如果误差项服从正态分布，ut～N（0，1），则方程（111）为稳态高斯VAR（q）模型的截距形势。它可以表示成如下的均值调整形势：

其中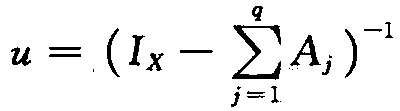，(www.daowen.com)

在实际研究中，如果时间序列受到区制变化的支配，且假设有N个区制，并且假设不可观测的区制已实现值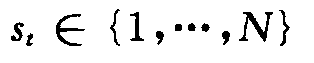是一个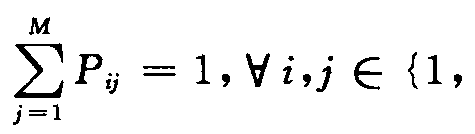离散时间和离散状态的马尔科夫链，其转移概率为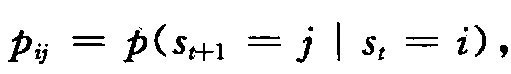…，M｝，则方程（2）可以写成阶数为q、区制数为N的马尔科夫区制转移式：

其中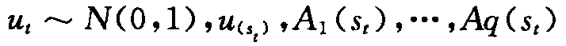是用来描述参数u，A1，…，A_q对于已实现区制s_t依赖的变参数函数。

在模型（3）的模拟过程中，如果一个区制发生一个一次性的跳跃，那么模型会随之改变，利用Hamilton给出的马尔科夫区制转移类模型的极大似然估计（ML）算法——期望最大化算法（EM）来估计模型（3）中一个区制转换到另一个区制的概率（转移矩阵），通过估计区制变量，t的取值概率来划分区制变量的主要状态。当然这会带来巨大的计算量，尤其是当区制N和变量个数q增大的时候，计算量将会呈几何指数级增加。因此虽然Krolzing H-M在1997年就已经提出此模型，但是其真正广泛应用却得益于国外一些学者将该模型程序化并将程序源码公布于网上。

本章将试图使用国外学者提供的程序包，利用中国的经济数据，对中国经济从一种状态（区制）向另一种状态（区制）转换的概率进行检验和预测，以此来对中国经济健康情况发出预警。首先，我们将金融风险的恶化程度设置为三种状态：低风险、中风险和高风险；然后我们定义：每当高风险区制的平滑概率估计值大于0.5的时候，为高风险状态，预警系统发出高风险警报信号，从而起到预警金融危机的作用。