4.3.3　供给实证结果分析

决策者对于洪灾保险供给意愿受不同风险特性影响，当所给予的情况不同，供给意愿也会随之改变，费率的估计也同样由于情况不同而改变。本节将采用同质性分析、回归模型进行保险公司对洪灾风险不确定下的参数估计，以下将说明不同风险情况下与决策间影响情形、模型回归式的参数选取、模型估计结果与比较分析:

一、风险特性与供给意愿的关系

（一）损失金额大小对供给决策的影响

（1）概率确定的情况下，损失金额大小对供给决策的影响。

在概率确定的情况下，当损失金额为2亿元时，同意核保人数为19人，不同意有4人，当损失金额为20亿元时，同意承保人数为24人，不同意有13人，当损失金额为100亿时，同意承保人数为11人，不同意有12人（见表4-4）。通过卡方检验得到估计值=6.1216，P=0.0468＜0.05，统计结果显著，表明在概率确定情况下，损失金额的大小对供给意愿会产生显著的影响（见表4-5）。

表4-4　概率确定情况下的保险供给决策

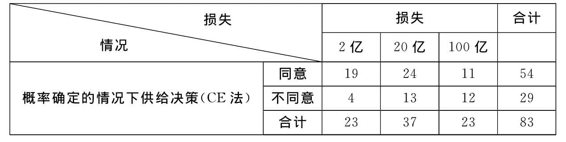
注:＊代表在统计水准5%时显著。

表4-5　CE法卡方检验

（2）概率不确定的情况下，损失金额大小对供给决策的影响

在概率不确定的情况下，当损失金额为2亿元时，15位同意承保，8位不同意承保；当损失金额为20亿元时，15位同意承保，22位不同意承保；当损失金额为200亿元时，7位同意承保，16位不同意承保（见表4-12）。通过卡方检验，估计值=6.072，P=0.0480＜0.05，统计结果显著（见表4-6），表示在概率不确定情况下，损失金额的大小也会对供给意愿产生显著影响。

表4-6　概率不确定情况下的保险供给决策

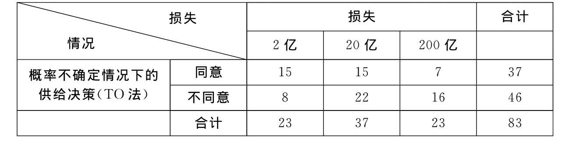
表4-7　GT法卡方检验

注:＊代表在统计水准5%时显著。

（二）概率的确定性与否将影响保险供给决策的比较

通过列联表的卡方检验估计值=20.0941，P=0.000＜0.001（见表4-8与表4-9），统计结果显著，不仅CE与GT法检验结果显著，而且CE与PE法检验结果的也显著。表示在概率确定的情况下，有助于提高洪灾保险的供给意愿。该检验符合Kunreuther在1995提出，保险公司对于概率不确定情况下的规避行为。如同Ho and Keller（2002）所提出保险公司对于获利的保险事项会害怕失去获利的机会，因此避免风险模糊事项。相对于洪灾保险而言，一般财产保险具有稳定获利。如果参与洪灾险，有可能会形成亏损，这也可能是造成受访者对不确定事项规避的原因之一。

表4-8　概率确定与不确定下的决策差异

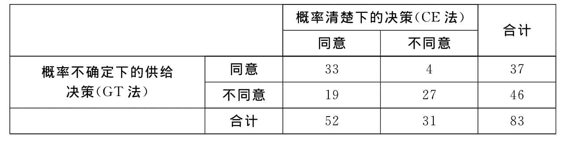
表4-9　CE/TO法卡方检验

注:＊＊＊代表在统计水准0.1%时显著。

二、洪灾保险费率与一般财产保险费率的比较分析

应用非预期效用理论分析洪灾保险费率与一般财产保险费率的差异。本文将“一般财产保险”定义为风险中立的风险型态，假定其保费率定为0.005，是标准值。通过与受访者估计的洪灾保险的费率进行比较，可评估保险决策者在不同情况下的风险定价。(www.daowen.com)

（一）GT法

在GT方法中，损失金额确定，而概率不确定的情况下，决策者能接受的最低保险费仍然高于标准值。

根据原假设:H 0:μ=0.005，备择假设:H 1:μ≠0.005，进行双尾检验。由表4-10的t检验分析，95%信赖区间［0.0047，0.0133］，未包含0，此外P=0.000＜0.001，因此应选择备择假设，拒绝原假设。即损失金额确定而概率不确定的情况下的费率与标准费率有明显的差异。

表4-10　GT法费率估计

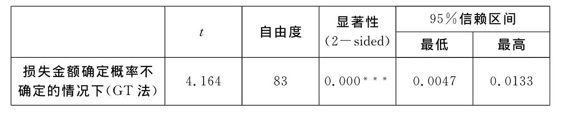
注:＊＊＊代表在统计水准0.1%时显著。

（二）CE法

在CE方法中，对决策者制定的费率进行检验，95%信赖区间^{［0.0042，0.0104］}，未包含0，此外，P=0.000＜0.001（见表4-11），因此应选择备择假设，拒绝原假设。也就说，在损失金额与损失概率都确定的情况下，供给决策者制定的保险费率与风险中立下的费率也有明显差异。这表明对于洪灾保险的风险认识确实与一般风险不同，影响保险决策定价模式。

表4-11　CE法费率估计

注:＊＊＊代表在统计水准0.1%时显著。

（三）GT/CE法

根据预期效用理论的假设，GT法与CE法的定价应该是一致的，即GT-Rate等于CE-Rate，通过检验，原假设:H 0:μTO=μCE

备择假设:H₁:μTO≠μCE，进行双尾检验。

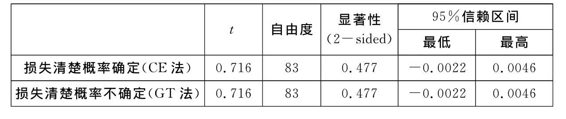
t检验分析，95﹪信赖区间^{［-0.0022，0.0046］}，包含0，此外P=0.477＞0.001（见表4-12），因此应拒绝备择假设，选择原假设。即损失金额确定概率不确定情况下的费率与损失金额与概率都确定的情况下的费率无明显差异。

表4-12　CE/GT法费率估计

三、PE法的概率认识

在决策者无特殊偏好的情况下，PE方法中概率应与CE方法中给予的概率相同。通过独立性t检验，个数为83，平均数为0.0028，标准差为0.0076，t值为2.980，P=0.004＜0.01（见表4-13），应拒绝原假设，选择备择假设。损失金额确定的情况下，决策者决定的主观概率与客观概率有明显差异，决策者认为洪灾发生概率高于专家学者评估的概率。这不仅表示决策者有明显风险规避特性，更表示决策者在定价或决定供给态度取决于心理的主观概率，符合猜测与猜测参考理论意义。

表4-13　PE法概率估计

注:＊＊代表在统计水准1%时显著。

四、影响保费水平决策的因素

为比较洪灾保险发生亏损或获利的概率，分别在确定与不确定时，影响受访者决定可接受保费水平特性的差异。以下分别以CE法与GT法的调查结果，应用三个回归分析检验不同变量影响保费费率水平决策的假设。其中，第一与第二个回归模型，直接采用CE法与GT法中调查所得的最小可接受费率水平进行OLS回归分析。

从上述回归分析结果，我们还发现受访者对于洪灾风险知觉成本的重视，进而支持洪灾具有的小概论、大损失的特性。该结果与许多通过实验法分析的文献，得出的结果非常接近（详可参见Camerer and Weber（1992）相关的文献回顾）。本文通过对核保与精算人员的实际调查^[1]，通过第一线的财产保险供给决策者资料得出的结论，可能更具有政策评估上的意义。