3.4.1　层析分析法AHP（Analytic　Hierarchy　Process）

层次分析法（AHP）是由美国著名的运筹学家T.L.Saaty教授于20世纪70年代末提出来的，它是一种灵活、简便并且实用的多准则决策方法。具体的算法步骤如下所示。

1.建立层次结构模型

应用层次分析法处理决策问题时，首先要把影响决策的各种因数层次化并构造出一个有层次的结构模型。层次结构的基本形式是由一个节点连结几个节点的树，如图3-11所示。

在这个层次结构模型下，复杂的各种因素被分为若干层次。上一层的每个因素由下一层用线段所连接的各个因素所决定。这些层次一般可分为三类:

（1）最高层，又称目标层。这一层只有一个因素，一般它就是决策的目标；

（2）中间层，又称准则层。这一层包括实现目标所需要考虑的各种因素，如果一些因素又可由其他一些因素所决定，则中间层可以由若干层组成；

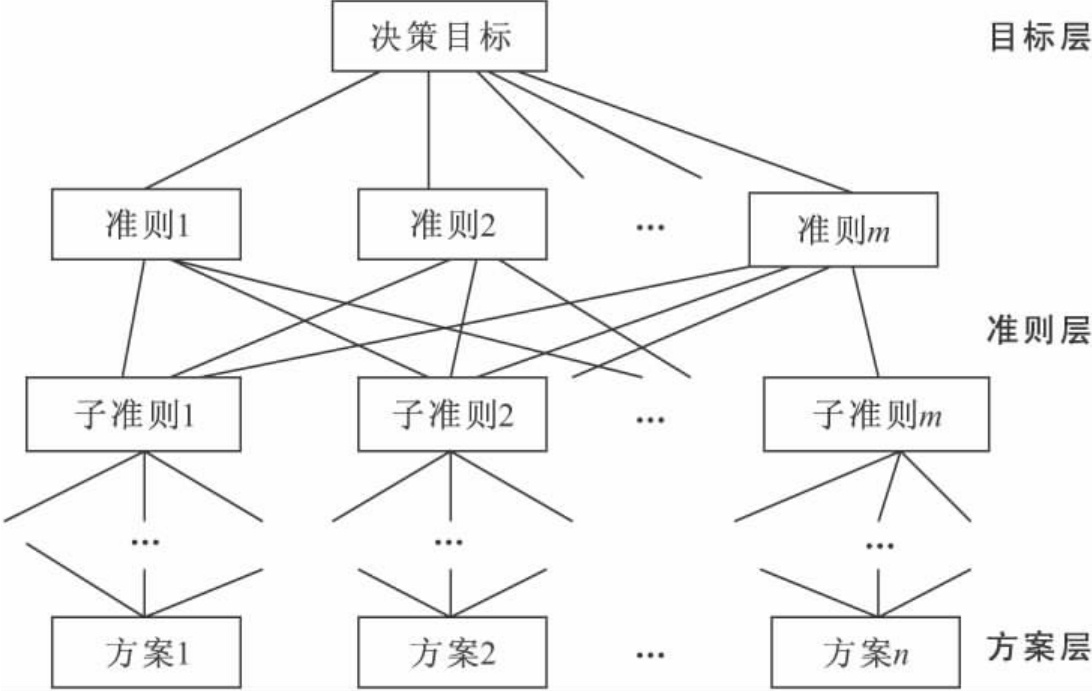
图3-11　层次结构图

（3）底层，又称方案层。这一层包括决策时可供选择的各种方案。

2.构造判断矩阵

通过对同一层次的指标两两进行比较，得到其对重要性的比值w_i/w_j，用这个比值来构造判断矩阵，如下式所示:

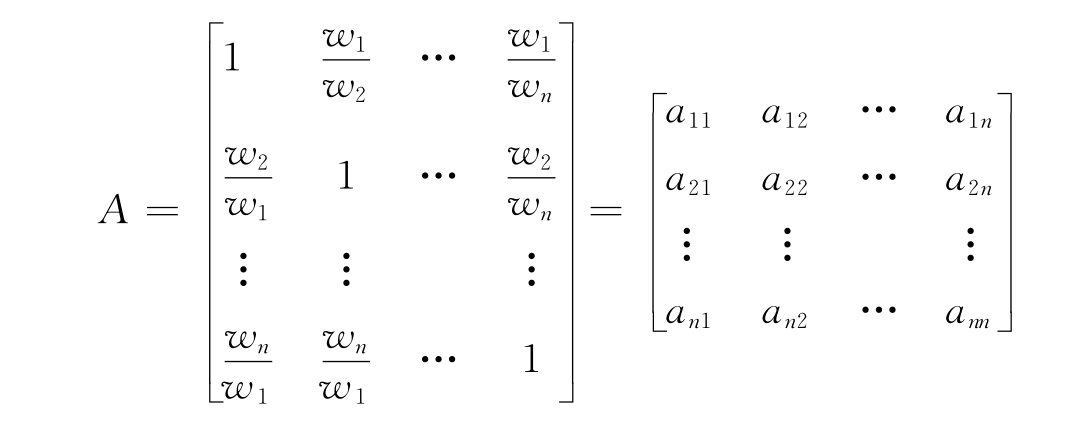
在上式中，判断矩阵A为n×n的方阵，它的主对角线上全为1。满足a_ij＝1/a_ji，i，j＝1，2，3，…，n，a_ij＞0，a_ij为i与j两个因素相对权重的比值，可以按照表3-2中1～9级比例标度法来对其重要性进行赋值。

表3-2　1～9级判断矩阵标度

3.权重值计算(www.daowen.com)

通常我们利用和法来计算权重值。

首先将A的每一列向量都归一化。公式为:

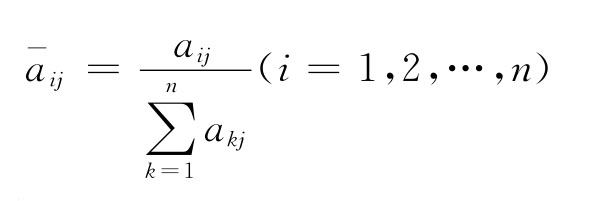
对上面按照列归一化的判断矩阵，再按照行求和:

最后再将向量-W＝［-W1，-W2，…，-Wn］^Τ归一化:

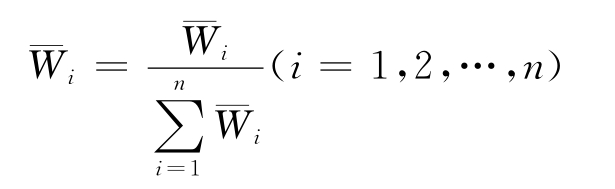
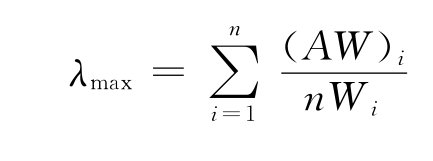
4.一致性检验

首先计算最大特征根:计算一致性指标:

计算一致性比例:

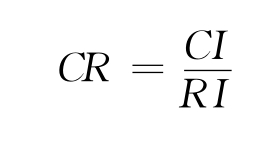
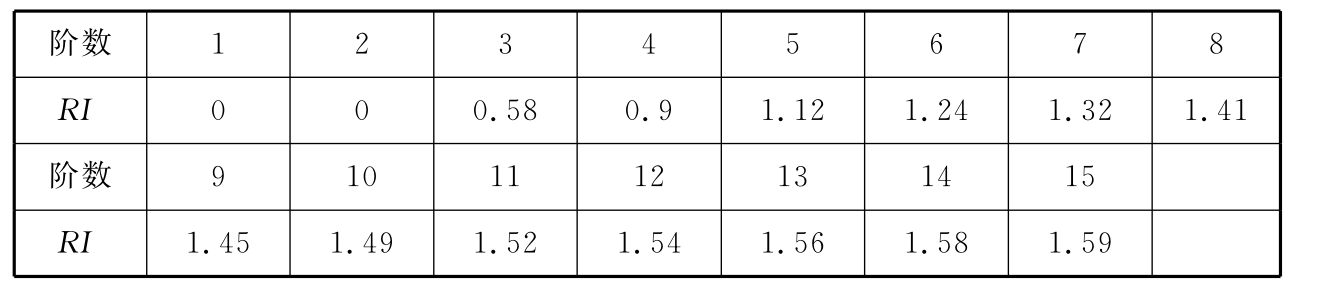
当CR＜0.1时，表明判断矩阵的一致性是可以接受的（表3-3）。

表3-3　一致性指标检验对照表