5.3.1　受众科技创新性的因子分析

1)因子分析方法

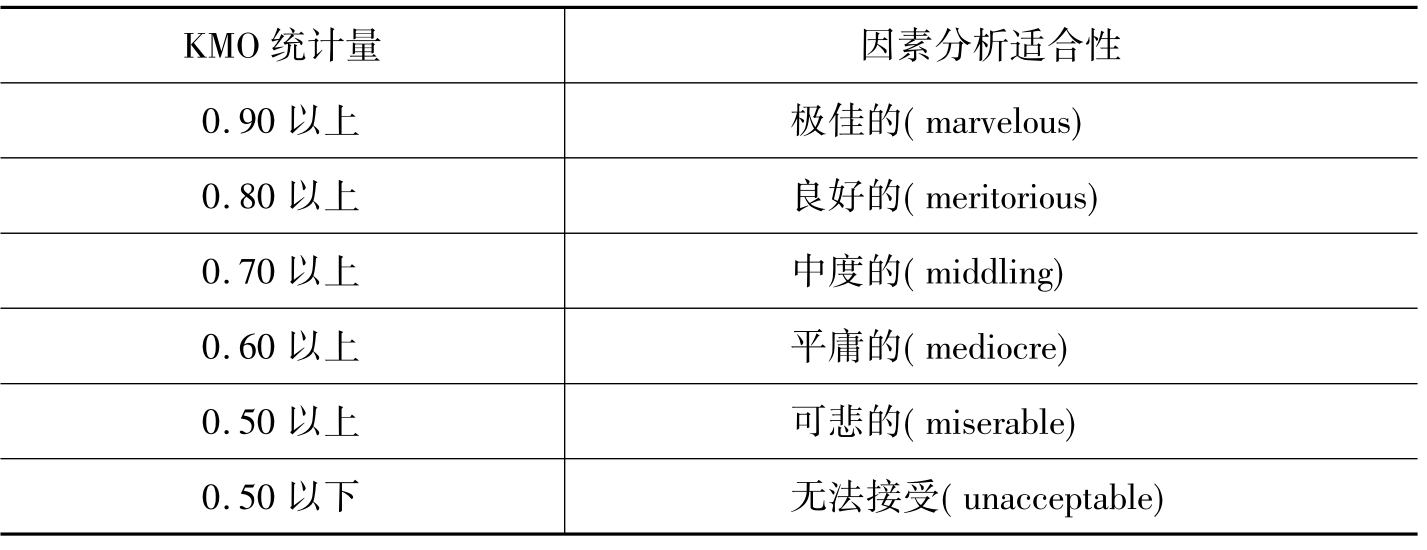
因子分析可以简化测量的那日，将复杂的共变结构予以简化，使得许多有相似概念的便利，通过数学关系的转换，简化成几个特定的同质性类别。进行因子分析需要达到一定的样本规模，Gorsuch(1983)建议样本数最少为变量数的五倍，且大于100。本研究的样本数为452个，达到样本要求。其次一组观察变量是否适合进行因素分析，主要与观察变量之间的相关情形有关，需要有较高的相关性才能进行因子分析。一般有几种方法可以判断相关矩阵的适切性，主要有Bartlett的球形检验(Bartlett's test of sphericity)、KMO量数(Kaiser-Meyer-Olkin measure of sampling adequacy)和共同性(communality)。Bartlett的球形检验需要显著大于0，才能适合因子分析。KMO量数大小判断准则如表5-10。共同性介于0与1之间，越高则表示该变量与其他变量可测量的共同特质越多。

表5-10　KMO统计量的判断原理^[2]

本研究具体因子分析的程序是:选取测量变量，以主成分分析法萃取共同变异因子，萃取出特征根大于1的因子，并以最大方差法(Varimax)转轴法对因子进行正交旋转。参照Tabachnica ＆ Fiedell(2007)提出因子负荷标准，剔除掉因子载荷小于0.45，其余测量项目即为相应因子的测量项目。

2)因子分析的过程

本研究将6个受众科技创新性变量应用上述的因子分析程序。首先进行了相关性验证，具体Bartlett的球形检验和KMO量数如表5-11，数据显示，KMO量数为0.797，适合对问项进行因子分析。近似卡方值为1 514.319，p值小于0.01，达到显著，表示适合进行因素分析。转轴后的因子负荷如表5-12，可以看到每个问项均在0.733～0.854之间，显示了较强的相关性。所以本研究的问项适合进行因子分析。

表5-11　KMO量数和Bartlett球形检验

表5-12　因子负荷

萃取方法:主成分分析。

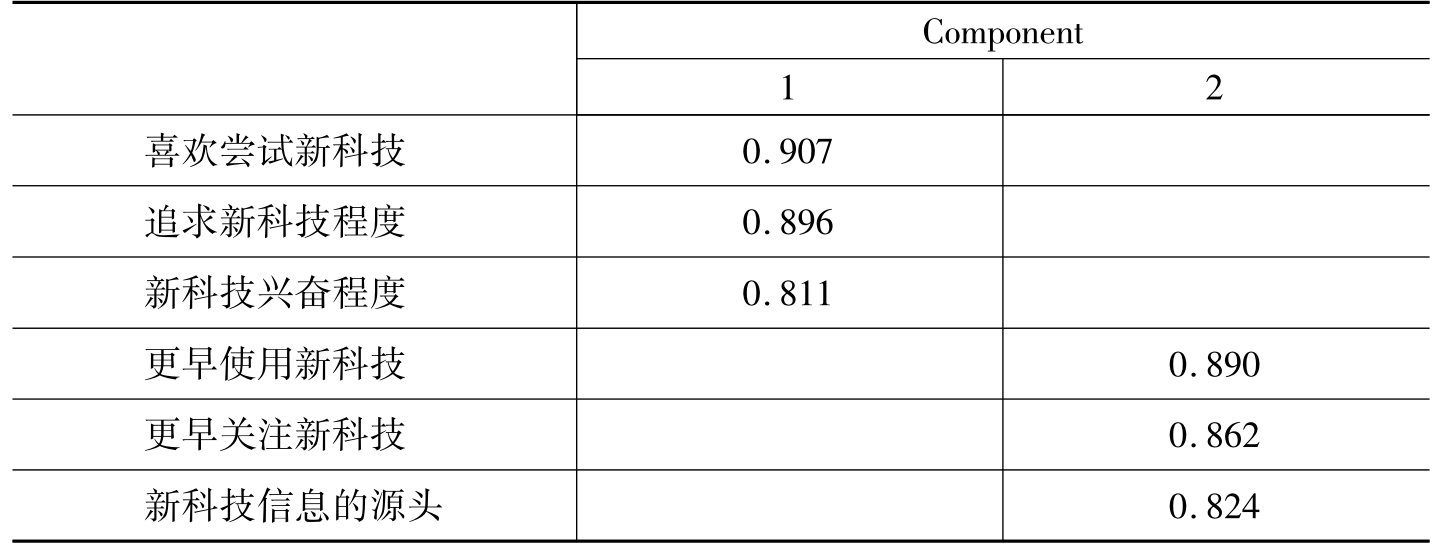
保留特征值大于1的因素，发现共有2个因子构面，分别可以解释58.110%和21.628的变量变异量，累计解释方差为79.737%，已超过40%的接受值，故认为保留的因子构面是合理的。经过转轴分析之后，发现这2个因子构面所包含的题项分别都超过3个问项，因此都能代表各个维度的表达特征，具体见表5-13。

表5-13　转轴后的成分矩阵(a)

3)因子分析的结果(www.daowen.com)

经过以上过程，最终得到两个主要因素，即两个因子构面，构成因素1的题目有3个，分别为TI1，TI2和TI3;构成因素2的题目有3个，分别为TI4，TI5和TI6。

表5-14　总解释方差量

萃取方法:主成分分析。

4)因子构面的信度分析

本研究除了将对整个量表进行信度评估外，还需对不同的分量表进行评估。本部分将对因子构面进行Cronbach'alpha信度分析，具体信度评估如表5-15。

表5-15　因子构面的信度分析

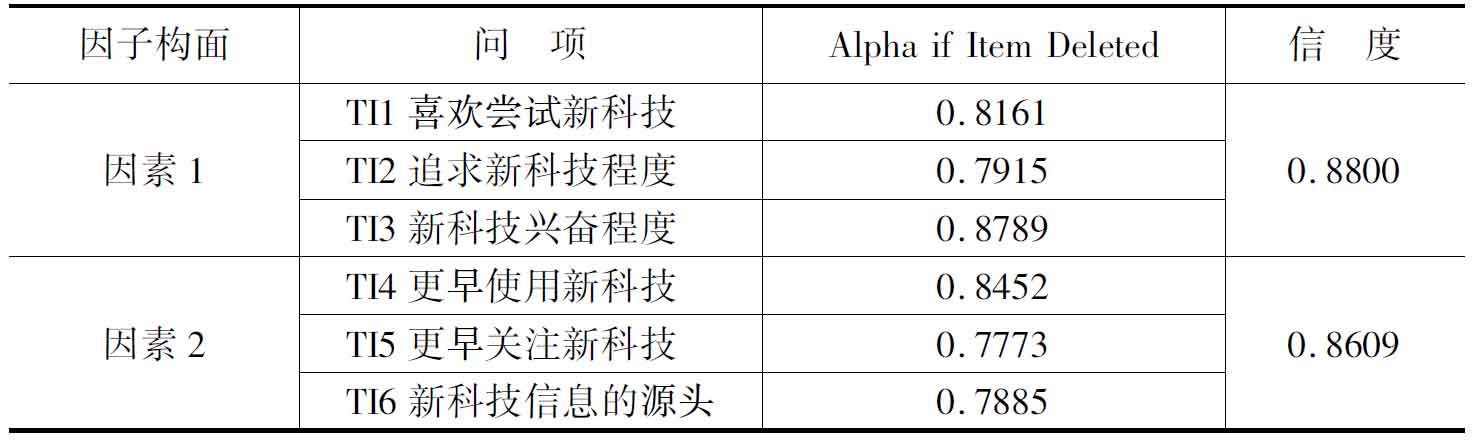
从表5-15可以看出，本研究科技创新性的因子构面的总体信度为0.8547，而萃取出的因素1的信度为0.8800，因素2的信度为0.8609。因此本部分的因子分析信度较高。

5)因子构面的命名

根据表5-16本研究对2个因子构面进行命名。

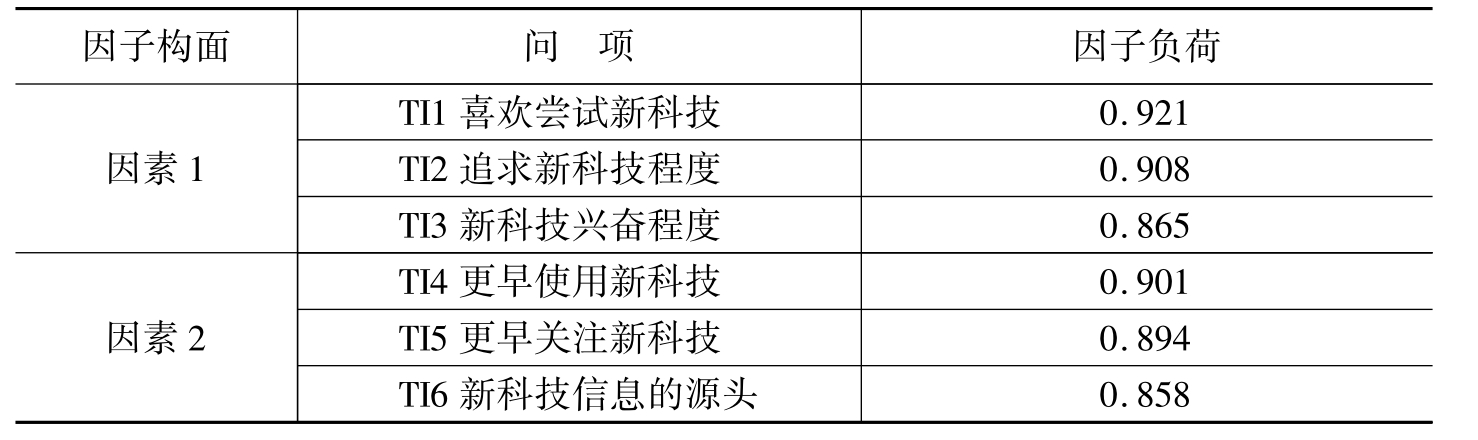
构成因素1的题目有3个，分别为TI1，TI2和TI3，这3个问项主要都是针对个人寻求刺激的冲动和对新奇的偏好，以及在此过程中的自我感官享受，可以说这3个问项测量的是个体本身的创新性问题，因此可以命名为自主创新因子。

构成因素2的题目有3个，分别为TI4，TI5和TI6，这3个问项主要反映的是社会心理，受众个体对与众不同的追求，因此可以命名为社会创新因子。

表5-16　因子构面的因子负荷