在对生产力进行衡量的过程中，涉及两个有所差别的概念：生产力水平和生产力水平的变化，生产力水平的衡量可用于在给定时点上对不同DMU之间的绩效进行比较。而生产力水平的变化则是指厂商或经济体的绩效随时间的变动。

对于经济分析者而言，了解生产率水平的情况非常必要，但是如果没有对不同DMU之间生产力水平的比较或者同一DMU在不同时点上的生产力水平比较，单独的生产力水平的数值所能说明的问题非常有限。因此，对生产力的衡量在很大程度上是对生产力水平变化的衡量，我们在本书中提到的生产力的衡量是指生产力水平变化的衡量，这里的生产力水平变化的衡量不仅包括同一DMU在不同时点上的生产力水平的变动，也包括同一时点上，不同DMU之间生产力水平的比较。

对生产力的衡量要用到TFP指数（全要素生产力指数），TFP指数是指在指数法的基础上发展起来的用于测算生产力变化的指数，很多经济学者从不同的角度、使用不同的方法定义了不同种类的TFP指数，本章我们将对TFP指数进行较为详尽的介绍。

在对TFP指数进行介绍的同时，我们首先对指数进行介绍，这是TFP发展的基础。指数是用于测定多个变量在不同场合下综合变动的一种特殊相对数。一方面，各类指数本身是一种非常重要的分析工具，指数可以用来比较随时间变化的价格与数量，也可以用来衡量不同厂商、行业、地区或国家的水平差异，它不仅被应用于经济效益、生活质量、综合国力、社会发展水平的综合研究，而且还是分析社会经济动态和景气预测的重要工具。另一方面，在经济研究的过程中，统计机构公布的各类数据往往不能直接使用，而需要进行一定的调整（如价格紧缩调整），而指数是对数据进行调整，从而得到可用于研究的数据的重要工具。

指数方法从产生到现在已经有300多年的历史。300多年间，涌现出了几百种不同的指数，其中最常用的有拉氏指数、派氏指数、Fisher理想指数、Tornqvist指数和Malmquist指数等。

拉氏（Laspeyres）指数和派氏（Passche）指数是较早提出的两类指数。拉氏指数由德国经济学家拉斯贝尔于1864年提出，他主张指数应按其基期水平进行加权；而德国经济学家的派许（1874）则认为指数应按其报告期水平进行加权，无论数量指数或价格指数均应采用报告期水平作权数。由于计算简单，拉氏指数和派氏指数在现实中得到了广泛的应用，大多数国家统计机构都以这两种指数为基础计算各种各样的指数，比如CPI。

以价格指数为例，拉氏价格指数的计算公式为：

其中表示基期第m种商品的价值占基期商品总价值的比重，称做价值份额，它的大小反映物品的相对重要程度。式（5．1）有两层含义：一是拉氏指数是以基期数量指标作同度量因素计算的报告期和基期m种物品价值总量的比率；二是它是以基期价值份额为权重的m种物品个体价格指数的加权平均值。

与拉氏指数不同，派氏指数则是使用报告期价值份额为权重：

其中，权数是第m种物品在时期t的价值份额。式（5．2）表明派氏价格指数是以报告期数量为同度量因素，分别以报告期价格和基期价格计算的两时期m种物品价值总量之比；或者说，是以报告期价值份额为权重的个体价格指数的加权平均值。

在某种意义上说，拉氏指数和派氏指数代表了两个极端，拉氏指数以基期（时期s）数量作为同度量因素，而派氏指数以报告期数量（时期t）作为同度量因素。如果每种产品的个体价格指数相同，那么这两个指数的值是一致的，也就是说，如果pmt／pms＝c，那么拉氏指数和派氏指数相同，均为c。而当不同产品的个体价格指数差别较大时，这两种指数的值也会有较大差别。由于这两种指数的权数选择都带有一定程度的极端性，这与现实经济状况是不相符的，因此对经济现象进行分析时，指数结果都会有所偏差。对同一经济现象进行分析时，拉氏指数通常会对经济现实做出偏高估计，派氏指数的估计值则会偏低。

与价格指数相对应，拉氏公式和派氏公式定义的数量指数分别为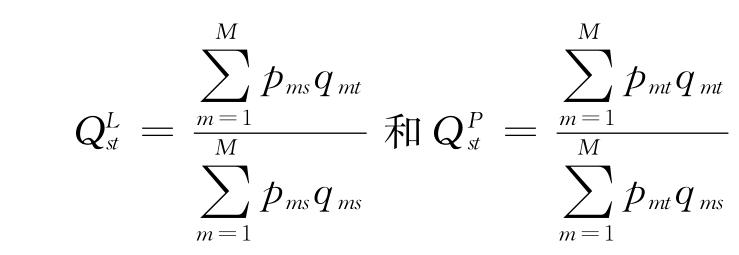：，拉氏和派氏数量指数的性质与其各自对应的价格指数相同，这里不再详述。

由于拉氏指数和派氏指数在对经济现象的评估中存在偏差，美国统计学家Fisher于1922年提出，先分别用拉氏和派氏公式编制总指数，然后对它们进行几何平均以得到一个新的指数。很明显，这一新的指数是对拉氏和派氏公式的折中，用它进行研究得到的结果一定介于拉氏指数和派氏指数的结果之间；与拉氏和派氏公式相比较，它的结果存在的偏差要小得多，同时这一指数还具有很多理想的统计性质与经济理论性质。正因为如此，这一新指数被称为“Fisher理想指数”（Fisher ideal Index）。

Fisher理想指数的计算公式为：

用Fisher理想指数计算的数量公式为

Fisher理想指数有着许多令人满意的统计和经济理论上的性质，能够满足一些重要的统计检验，如时间转换检验和因子转换检验等（而拉氏指数和派氏指数本身都不能通过这些检验）。同时由于Fisher理想指数体系融综合指数的两套分析体系于一体，兼顾并中和了拉氏指数和派氏指数由于权数选择不同而导致的差异性，从而避免了综合指数的失真性。正是由于Fisher指数所具有的良好性质，它在经济统计中被广泛应用，有着很大的吸引力。尽管Fisher指数是“理想的”，但它仍然存在一些不足之处：首先，Fisher指数要求它的数据达到能计算拉氏指数和派氏指数的要求，数据需求量大。这不仅会增加核算费用，而且会由于工作量的加大而导致计算和结果公布的延迟。其次，Fisher指数不像拉氏指数和派氏指数那样容易理解。拉氏指数和派氏指数可以简单地解释为计量指定的一揽子货物和服务的价值变化，而Fisher指数不可以。再次，Fisher指数不具有可加一致性，即使对于最基本的年度间数据变化也是如此。这一缺陷严重制约了它在核算框架中的应用。

Tornqvist价格指数定义为个体价格指数的加权几何平均值，其中权数为时期s和时期t的价值份额的简单算术平均值，即：

其中，ωms和ωmt分别为第m种物品在基期s和报告期t的价值份额。Tornqvist指数一般写成它的对数形式：

这种对数变换形式为实际计算提供了方便。对数形式下的Tornqvist指数是对数形式的个体价格指数的加权平均。由于第m种产品价格的对数变化，

代表了第m种产品价格变化的百分比，因而对数形式的Tornqvist价格指数表现的是总体价格的增长率。

相应地，Tornquist数量指数为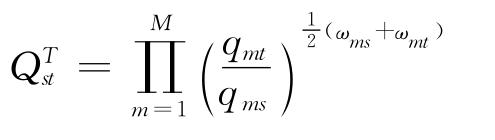

其对数形式为

我们在本书1．3中讲过，衡量全要素生产力的方法多种多样，而指数法由于其特殊的优势在经济研究和社会生活中得到了最为广泛的应用，因此本书介绍的衡量全要素生产力的方法是指数法。首先，指数法的最突出优点是避开了具体函数形式的制约，可以通过统计资料直接衡量生产力指数，从而也避开了生产函数法等经济计量学方法常常可能遇到的多重共线性、解释变量内生等问题。其次，利用指数法衡量生产力增长的分析资料容易获得，理论原理简单明了。对于任意DMU（企业、行业、国家或地区），只要能够获得其任意两个时期的投入产出数量和相应价格（或价值份额）资料，就可以计算相应的生产力变化，方法简单，易于理解。再次，指数法可用于解决多产出和多投入问题，可以对使用不同技术进行生产的单位进行比较。因此指数法在实践中得到了广泛的应用，而指数法在发展过程中也不断完善，产生了多种多样的全要素生产力指数。

全要素生产力指数的具体形式虽多，但都必须反映出全要素生产力的基本性质，那就是：如果产出不变，而相应地投入使用量减少了，那么全要素生产力提高了；如果保持投入不变，而产出增加了，那么全要素生产力也提高了。因此，假定如果我们用函数F（xt，yt，xs，ys）表示TFP指数（其中xt、xs、yt和ys分别为时期t和时期s的投入和产出），那么任何有意义的TFP指数应满足如下性质：

这意味着TFP指数关于y的齐次次数为＋1，关于x的齐次次数为－1。当我们选择一种方法来计算TFP指数时，所得到的指数需要满足式（5．8）所示的性质。

Hicks和Moorsteen（1961）提出了一种简单使用投入增长和产出增长来衡量全要素生产力变化的指数，如下式所示：

由此我们可以清楚地看到，如果产出增长的幅度大于投入增长的幅度，那么HM TFP＞1，全要素生产力水平有所提高；反之，如果产出增长的幅度小于投入增长的幅度，那么全要素生产力的水平就会降低。产出量指数和投入量指数可以使用在前面提到的几种指数进行计算，由于各种指数计算方法的性质不同，在具体应用过程中，应根据所研究问题的具体情况选择合适的指数计算方法。

HM TFP指数的经济意义简单明了，具体操作过程也比较简单，但该指数存在明显的缺陷，那就是对生产力变化的来源缺乏解释力。

设Rs、Rt、Cs和Ct分别表示给定厂商在时期s和时期t的收益和成本。利润率可作为厂商全要数生产力水平的衡量，而剔除了投入与产出价格因素影响的利润率可作为不同厂商之间全要素生产力水平的比较。同理，可以通过厂商在时期s与时期t的利润率的比较（前提是剔除了从时期s到时期t的价格变化因素的影响）得出厂商的生产率变化情况，以及基于利润率的TFP指数。在时期s，关于投入、产出数量基期价格的数据可由（xs，ys，ps）和（xs，ys，ws）给出，在时期t的相应数据由（xt，yt，pt）和（xt，yt，wt）给出。令分别表示经过价格调整后DMU在时期s和时期t的收益与成本，则基于利润率的TFP指数可定义为：

由于式（5．10）的TFP指数提出了价格因素的影响，因此从时期s到时期t的全要数生产力变化来源于技术变化与效率变化。

其中产出价格指数和投入价格指数可以通过所观测到的数据利用前面所述的指数公式求得。前面所述的四种指数计算方法各有其不同的特性，因此选用哪种指数计算方法也会是求得的基于利润的TFP指数带有该指数计算方法的特性。由于Fisher理想指数具有众多优良的特性，而Diewert也于1992年证明了用Fisher理想指数求得的基于利润的TFP指数对于一个可塑的可变利润函数是准确的，是一个超越指数。因此，Fisher理想指数在计算基于利润的TFP指数的过程中得到了广泛的应用。

Malmquist TFP指数是由Caves，Christensen和Diewert（1982a，1982b）在其所写的两篇很有影响的文章中引进的。在这两篇文章中，CCD利用Malmquist投入和产出距离函数定义了TFP指数，称为Malmquist TFP指数，这种构造TFP指数的方法称为CCD方法。该指数是通过在时期s到时期t所观测到的投入产出向量来衡量的，CCD方法是运营在参照技术下，通过时期s到时期t的产出观测值以及xs、xt所能生产的最大产出水平（保持产出组合不变）之间的比较来衡量生产力的。由于距离函数有投入导向和产出导向之分，因此Malmquist TFP指数也可分为投入导向和产出导向。而Malmquist TFP指数可进一步分解为技术变动因素和效率变动因素，进而可以对生产力变化的来源进行较好的解释。

从本质上说，Malmquist生产力指数可以归类于生产力变化衡量的指数法，但它与其他指数又有着很多的不同之处。实践中，研究者常把Malmquist指数与边界分析技术结合起来运用，并在此基础上实现对生产力增长的分解和测算技术效率，这是它与其他指数方法相比较的一大优势。因此我们在下一节单独对Malmquist指数进行详细分析。

前面所讨论的三种衡量生产力变动的方法是利用了生产力变化直观概念的衡量体系，一旦得到了生产力变动的数值，就需要对这一数值进行解释，分析生产力变动的来源（技术的进步还是效率的提高），这类方法被称为“自上而下”的方法。在这种方法中，生产力变化的一些来源可能得不到适当的解释，在对结果的阐释上也有一些困难。

为了针对这一情况做出改进，Balk（2001）提出了一种“自下而上”的方法，试图确定所有的生产力变化来源。这种方法从所有生产力变化可能的来源开始，使用最合适的方法对每一个来源进行衡量，最后把它们合成起来得到出生产力变化指数。

Balk指出了生产力变动的四个来源：技术变化（TC）、效率变化（EC）、规模效率变化（SE）和产出混合效应（OME）或者投入混合效应（IME）。

技术变化是生产力变化的重要来源。我们通过DMU在时期t利用给定投入向量生产多于（或少于）时期s可行的产出水平的能力来衡量一个DMU的技术变化。对于投入产出向量（x，y），可以利用产出距离函数，通过比较产出向量y在时期s和时期t的生产前沿上的径向投影来衡量技术变化，如下式：

其中，式中的下标“o”表示产出导向。在进行测算的过程中，投入产出向量（x，y）既可以选择时期s的观测值，也可以选择时期t的观测值，相对应地就有两种测算形式。因此在对技术变动进行测算时，两种测算形式的几何平均值：

技术效率变化也是生产力变化的重要来源。在产出导向的情况下，距离函数只与技术效率的值是相等的，因此技术效率变化可以由下式来表述：

各DMU可以通过变动它的运营规模使得DMU运营于生产技术最优规模处，进而提高其生产率。要考察一个DMU由于运营规模的对其技术效率的影响，我们可以利用观测到的投入产出数据构造一个规模报酬不变（CRS）的生产前沿和一个规模报酬可变（VRS）的生产前沿，通过比较某一时期所考察DMU 与CRS生产前沿的距离和与VRS生产前沿的距离来确定该DMU的规模效率。则DMU在时期t的规模效率如下式所示：

其中，TE＊t（x，y）是DMU相对于CRS生产前沿的技术效率。规模效率的数值总是位于0和1之间，如果规模效率值为1，则说明DMU的规模是有效的。

得到了规模效率的计算公式，我们可以进而得到在时期s和时期t规模效率变动的计算公式：

式（5．15）衡量了相对于特定的产出向量y，分别使用投入向量xs和xt得到的规模效率值的比值。如果该比值大于1，则说明时期t相对于时期s更具有规模效率。我们还需要看到，在式（5．15）的计算中，特定产出向量y既可以使用时期s的数据，也可以使用时期t的数据，而测算规模效率时也同样既可以选择时期s的技术又可以选择时期t的技术，因此对两种选择进行几何平均，便得到了更为合理的关于规模效率变动的测算：(www.daowen.com)

产出混合效应。式（5．16）是分别定义在产出向量ys和yt上的规模效率变动几何平均值，但是并没有考虑到产出向量从时期s到时期t的变化对规模效率的影响，而产出混合效应正式描述对于特定投入向量x，产出向量由ys变为yt对规模效率变动的影响。Balk给出了测算产出混合效应的公式：

式（5．17）是参照时期t的技术来计算的，同规模效率变动的情况一样，也可以参照时期s的技术来计算，因此，将二者进行几何平均，便得到了如下公式：

在TFP变化的来源都可以得到衡量的前提下，Balk提出的这种从生产力变化来源衡量的TFP指数则为上述的技术变化、技术效率变化、规模效率变化和产出混合效应的乘积：

Malmquist数量指数由瑞典经济学和统计学家Sten Malmquist于1953年首次提出，当时是用来分析不同时期的消费变化；比照Malmquist数量指数，Caves，Christensen和Diewert（1982）首先将该指数用于生产力变化的衡量，分别构造了产出导向和投入导向的Malmquist生产力指数；此后与Charnes et al．（1978）建立的DEA理论相结合，在生产力衡量中的应用日益广泛。1994年，Fare，Grosskopf，Norris和Zhang建立了用来考察全要素生产力增长的Maimquist生产力指数，进而应用shephard距离函数将生产力增长分解为技术进步与技术效率变动，该方法不仅可以度量全要素生产力的逐期变化动态，而且可以将这一变化更进一步分解为技术进步、纯技术效率变动和规模效率变动等几个重要组成部分。

Malmquist指数是建立在距离函数基础之上的，距离函数有产出导向和投入导向之分，因此Malmquist指数也可以分别从产出和投入两个导向来定义。

（1）产出导向Malmquist TFP指数

产出导向生产力指数的衡量是通过比较所考察DMU在时期s和时期t的投入产出向量与特定的生产前沿的距离进行比较而得到的。所用到的距离函数当然都是产出导向距离函数，计算公式如下：

产出距离函数表示了在特定的投入水平下，DMU的产出水平与s时期的技术前沿上的产量的比值；而产出距离函数dso（xt，yt）则表示了在特定投入水平下，DMU在时期t的产出水平与s时期的技术前沿上的产量的比值。这样一来，式（5．20）就反映了从时期s到时期t DMU生产力变动的情况。由于时期t的特定投入产出向量并不一定位于时期s的技术前沿的下方，因此有可能大于1。当大于1时，表明DMU在时期t的生产力水平相比于时期s有所提高；如果小于1，则表明DMU的生产力水平有所下降。

式（5．20）中是使用时期s的观测数据所确定的技术前沿作为参考，同样，我们也可以采用时期t的观测数据确定的技术前沿作为参考，从而得出另外一个TFP指数，如下式所示：

选择不同时期的技术前沿作为参考会使结果产生差异。为了消除由于参考技术前沿的选择而带来的偏差，Malmquist TFP指数定义为二者的几何平均值：

大于1，表明厂商在时期t的生产率水平与时期s相比有所提高小于1，则表明DMU的生产力水平有所降低。在生产技术具有规模报酬不变的情况下，生产力的变化有可能来自于技术变化或者技术效率的变化。Malmquist TFP指数很容易进行进一步的分解，式（5．22）经过简单的数学变换，可以写成如下形式：

式（5．24）是DMU在时期t和时期s的技术效率值的比值，反映了技术效率的变动，而式（5．25）则反映了从时期s到时期t技术前沿的变动。这样一来，在确定了Malmquist TFP指数的数值之后，就可以进一步分析生产力的变化在多大程度上是来自于技术前沿的变动和在多大程度上来自于技术效率的变化。

（2）投入导向的Malmquist TFP指数

投入导向的Malmquist TFP指数与产出导向的Malmquist TFP指数的构造方式相同，只不过使用的是投入导向的距离函数，从投入缩减的角度来考察生产力水平的变动。

选择时期s的生产技术前沿作为参考技术前沿，TFP指数可写成如下形式：

同样，若选择时期t的技术前沿作为参考技术前沿，则TFP指数可写成如下形式：

出于与产出导向的情况下同样的考虑，投入导向的Malmquist TFP指数也同时采用时期s和时期t的技术前沿作为参考，即取式（5．26）和式（5．27）的几何平均值，如下所示：

同产出导向的情况相同，投入导向的Malmquist TFP指数也可以分解为效率变化和技术前沿变化两个部分，具体过程同产出导向的情况相同，这里不再赘述。

（1）投入导向与产出导向Malmquist TFP指数的关系

投入导向和产出导向的Malmquist TFP指数在计算的过程中分别使用了投入距离函数和产出距离函数，因此不同导向的Malmquist TFP指数在数值上是有所不同的。如果潜在生产技术在时期s和时期t都呈现出规模报酬不变的性质，则投入导向和产出导向的Malmquist TFP指数的结果是一致的。

（2）Malmquist TFP指数与生产技术的规模报酬效应

上面已经介绍了Malmquist TFP指数可以分解为技术变动和技术效率的变动，因此可见Malmquist TFP指数只考虑了全要素生产力变动的两个来源。由Balk的理论可知，全要素生产力的变动有四个来源，Malmquist TFP指数并未考虑规模效率变动和产出混合效应两个来源。在生产技术是规模报酬不变的情况下，Malmquist TFP指数可以准确地衡量出全要素生产力的变化，而如果生产技术是规模报酬可变的，Malmquist TFP指数对现实生产力变化测算的结果则会产生偏差。

针对这一情况，Fare等（1994）提出将技术效率变化进一步分解为纯技术效率变化和规模效率变化，如下式所示：

其中，PTEC为纯技术效率变化，是时期t和时期s在规模报酬可变条件下的技术效率值的比值；SEC则表示规模效率的变化。Fare等人将技术效率变化分解为纯技术效率变化和规模效率变化的做法得到了广泛的应用，但也存在一些问题，因为在计算Malmquist TFP指数时所用的距离函数是在规模报酬不变的假设下求得的，而在对技术效率变动的分解时需要在规模报酬可变假设下求得距离函数。对于同一个生产技术，在计算过程的前后对其规模报酬性质的假设不一致，这在很大程度上影响了这种分解法的科学性。

要对Malmquist TFP指数的数值进行估算，则需要首先计算出构造Malmquist TFP指数的四个距离函数的数值，在对距离函数值的估算中，最常用的是DEA方法和SFA方法，我们接下来以产出导向的情况为例分别予以介绍。

（1）使用DEA方法估算

对于距离函数和的计算，与本书前面介绍的用DEA方法测算效率值的过程相同，可通过下面两个线性规划过程求得：

对于距离函数和的计算，仍然使用DEA线性规划的方法，只需将约束条件进行简单调整即可：

这里有两个问题需要说明一下：

1）在上述四个线性规划中，使用的都是规模报酬不变效应，这样可以确保得出的Malmquist TFP指数满足式（5．8）描述的性质。而若要将Malmquist TFP指数分解得到的技术效率进一步分解为纯技术效率和规模效率的时候，则需要在规模报酬可变的情况下分别计算厂商在时期s和时期t的距离函数，具体过程只需在式（5．31）和式（5．32）的约束条件中加入约束条件即可。

2）在式（5．33）的线性规划计算的是时期s的投入产出向量与时期t的观测数据构造的技术前沿的距离，由于时期s的投入产出点不一定位于时期t的技术前沿的下方，也有可能位于其上方，因此的值有可能大于1，同样的道理的值也有可能大于1。

（2）使用SFA方法估算

Malmquist TFP指数所需的距离函数值同样可以用SFA的方法来计算。本书所给出的方法是以Fuentes，Grifell－Tatje和Perelman（2001）与Orea （2002）提出的超越对数形式的生产函数方法为基础的。我们要考察的超越对数形式的随机生产前沿定义如下：

其中，yit表示第i个DMU在第t年的产出；xkit表示第k个投入量；t表示技术变化的时间趋势；β表示要估计的位置参数向量；vit表示随机误差，假定vit与 uit相互独立并且同分布，服从的正态分布；uit表示技术无效因素。

上述模型具有时间趋势t与投入变量的交互作用，这考虑了非中性技术变化。

可利用前面章节概括的方法来预测每一年度每个厂商的技术效率，也就是在给定eit＝vit－uit值下，我们得到exp（－uit）的条件期望。因为uit是一个非负的随机变量，所以技术效率的预测值都是介于0和1之间，取值为1时表示完全技术效率。

技术效率的测算结果如式（5．36）所示：

其中eit＝vit－uit，可用于计算效率变化成分，即通过dto（xit，yit）＝TEit与我们计算效率变化指数如式（5．37）所示：

第i个DMU从时期s到时期t的技术变化指数可以从估计的参数中直接计算得到。一种方法是，利用第i个DMU在时期s与时期t的数据，求出生产函数对时间的偏导数。从而两个临近的时期s和时期t的技术变化指数成为这两个偏导数的几何平均值。当涉及超越对数函数时，上述结果等价于求对数导数的代数平均值的指数函数。也就是：

这种测算可以直接同式（5．25）进行比较。然后，由式（5．37）和式（5．38）得到技术效率变化指数和技术变化指数。

[1]本章参考黄镜如，付祖坛，黄美瑛．绩效评估——效率与生产力之理论与应用．新陆书局股份有限公司，1997和Coelli，T．，D．S．Prasada Rao and G．E．Battese．An Introduction to Efficiency and Productivity Analysis．Boston：Kluwer Academic Publishers，1998（2）