1.模糊评价流程图

根据前面所建立的指标体系，建立如图12-3所示的递阶层次结构。

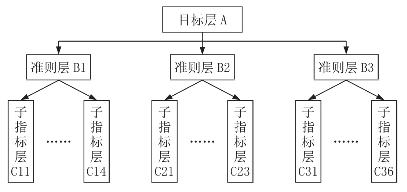
图12-3　递阶层次结构图

根据模糊综合评价理论，结合递阶层次结构，整体评价衔接线网发展水平，此评价过程是一个多级评判过程，第一级为准则层，该级各项指标的确定就可随之得到最后的评价结果；第二级为指标层，通过该层的计算可以得到第一级各指标的数据。通过分析可知，从第一级到第二级属于级级分解的过程，在具体进行方案综合评判时应先从第二级开始。模糊评价流程如图12-4所示。

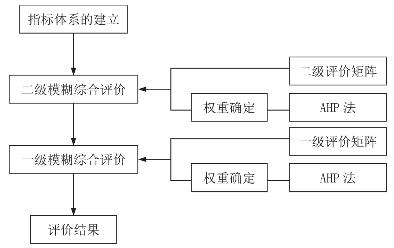
图12-4　模糊评价流程图

2.权重的确定

首先由专家组成员根据指标间相对重要程度给出指标的重要度矩阵，运用层次分析法计算出指标的相对重要度权重。又由于层次分析法在构造判断矩阵中，用1～9标度来定量表示指标间相对重要程度，这种判断尺度定义虽然本身有其合理、科学的一面，然而在实际应用中，都往往很难设计出使专家一看就懂的调查表格，或者专家和决策者都难以适应1～9标度，即使可以表示出来，也往往难以准确反映决策者的感觉和判断，出现较严重的不一致现象，从而使决策者的可信度下降。针对这些问题，本文采用改进层次分析法来计算指标的专家个体权重向量，即权重评分标准为：

表12-17　改进AHP法专家评分标准

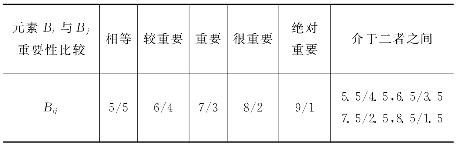
其中，矩阵的一致性调整与AHP法并无差异，只是进行一致性调整时采用的修正值R.I不同而已。

把每个专家给出的判断矩阵求得的权重向量称专家个体权重向量，记U=（U1，U2，…，Um），Ui=（Ui1，Ui2……Uin），其中Uij为第i个专家确定的第j个指标的权重，m为专家个数，n为指标个数。

考虑到每位专家所处的社会环境不同，个人的经历、经验、文化背景、要求、偏好均不尽相同，从而给出的判断矩阵，求出的专家个体权重向量也不一定相同，那么每位专家的个体权重向量对综合权重起多大的作用，也即每位专家的权重是多少。目前，对个体权重向量权重系数的确定，往往根据专家个人的声望、权威性等因数人为确定，然而，这种确定是不客观也比较难进行的，因此本研究在改进层次分析法所计算出的个体权重向量基础上采用聚类分析的方法，对专家个体权重向量进行聚类分析，然后根据聚类结果，通过计算，对每位专家分别赋权，再将个体权重与专家权重加权平均求得指标相对重要度权重Wj1（j表示第j个指标）。聚类分析法确定专家权重系数的具体操作过程如下：

通过对个体权重向量的聚类分析，将个体权重向量划分为不同的类别。假设有m个体权重向量聚集成t个类别（显然有t≤m），第p个类（p≤t）包含个体排序向量为φp个（φp称为类别Ωp的类容量），不妨进一步假设第i个体权重向量属于第p类Ωp，类别Ωp中包含的个体权重向量个数φp与个体权重向量总数m的比值，称为个体权重向量Ui的置信因子，用αi表示：

由式（12-30）知，同一类的个体权重向量具有相同的置信因子，也即同一类的个体权重向量所表达的信息可以认为是相似的，而属于不同类别的个体权重向量所表达的评价信息可以认为不相似，由此有以下权重系数确定原则：

类容量较大的类中个体权重向量所表达的评价信息符合较多评价者的意见，对应的专家应赋以较大的权重系数；类容量较小的类中的个体权重向量所对应的专家应赋以较小的权重系数。专家i的权重系数λi与个体权重向量Ui的置信因子αi成正比

进一步推导有

即有

因为属于同一类的个体权重向量有相同的置信因子，所以

由（12-33）、（12-34）两式得

式中：φp为个体权重向量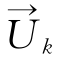所在Ωp类容量；λk为专家k的权重。(www.daowen.com)

因此：

3.建立Fuzzy评价矩阵R

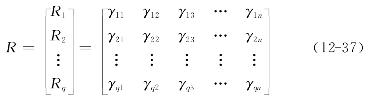
R称为Fuzzy评价矩阵，其中γij为隶属度，即第j个指标隶属于第i个评语的程度，q为评语个数。隶属度的确定采用隶属函数来计算。

由于专家打分的综合结果所隶属的评语在标准区间边界处不是绝对的，因此，在区间边界处，指标隶属度函数的确定应该采用清晰等级划分区间模糊化的方法。

由于隶属度与评价分值之间的关系在每个区间内并不是单调的，因此采用中间型隶属函数比较合理，而正弦曲线能较准确地反映相邻分数之间的隶属度差别，故隶属函数采用正弦曲线，见图12-5：

图12-5　指标隶属度函数图

将评语分为“极小、较小、一般、较大、极大”五个等级，则模糊等级的解析式为：

其中：r1j——指标隶属于“极小”的隶属度；

r2j——指标隶属于“较小”的隶属度；

r3j——指标隶属于“一般”的隶属度；

r4j——指标隶属于“较大”的隶属度；

r5j——指标隶属于“极大”的隶属度；

uj——指标分值。

4.最终评价结果最大隶属有效度检验

一般情况下采用综合评判结果向量所提供的信息，利用最大隶属度原则，对指标所属评语做出判断。但最大隶属原则，损失的信息太多，有效程度不高，因此在利用此方法时必须检验其有效度，检验量α为：

式中：q——评语个数；

β——评语集中最大分量所占比重；

γ——评语集中第二大分量所占比重；

rj——评价结果隶属于第j个评语的隶属度。

当α=+∞时，可认为施行最大隶属度原则完全有效；当1≤α＜∞时，可认为施行最大隶属原则非常有效；当0.5≤α≤1时，可认为施行最大隶属原则比较有效，其有效程度即α值；当0＜α＜0.5时，可认为施行最大隶属原则是最低效的；而当α=0时，可认为施行最大隶属原则完全无效。