灰色关联投影法是一种多因素统计分析方法，其核心是以各因素数据为依据计算投影值。

考虑多指标决策域的集合：

A=｛方案1，方案2，方案3，……，方案n｝=｛A1，A2，A3，…，An｝

设V是指标因素的集合：

A=｛指标1，指标2，指标3，……，指标m｝=｛V1，V2，V3，…，Vm｝

方案Ai对指标Vj的指标值记为Yij（i=1，2，3，…，n；j=1，2，3，…，m）

通常，指标有正向指标和负向指标之分，正向指标是属性值愈大愈好的指标，负向指标是属性值愈小愈好的指标。

当因素指标Vj为正向指标时，Y0j=max｛Y1j，Y2j，Y3j，…，Ynj｝

当因素指标Vj为负向指标时，Y0j=min｛Y1j，Y2j，Y3j，…，Ynj｝

则称Y=（Yij）（n+1）＊m（i=1，2，3，…，n；j=1，2，3，…，m）为方案A对指标集V的决策矩阵。

为了消除量纲不同所带来的不可公度性，决策之前首先应对评价指标进行无量纲化处理。

记Y′为Y的初始化序列：

当因素指标为正向指标时：Yij′=Yij/Y0j（i=1，2，3，…，n；j= 1，2，3，…，m）　　（12-10）

当因素指标为负向指标时，Yij′=Y0j/Yij（i=1，2，3，…，n；j= 1，2，3，…，m）　　（12-11）

经过初值化处理以后，很显然Y0j′=1（j=1，2，3，…，m）即为理想方案，以Y0j′为母元素，以Yij′（i=1，2，3，…，n；j=1，2，3，…，m）为子元素，就可以得到其他方案与理想方案的关联度。

记（S，Γ）为灰色关联空间，ξ为特定关联映射，rij为子因素Yij′（i=1，2，3，…，n；j=1，2，3，…，m）关于母因素Y0j′（j=1，2，3，…，m）的关联度，rij=ξ（Y0j′，Yij′），则有：

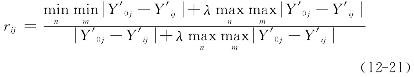(www.daowen.com)

式中，常数λ称为分辨系数，它的作用在于调整比较环境的大小，即将比较环境缩小改变，当λ=0时，环境消失；当λ=1时，环境“原封不动”保存着，通常，区λ=0.5。

称有（n+1）m个r组成的矩阵为多目标灰色关联度判别矩阵F。由于一个设计方案是由m个因素指标所确定的，它构成m维因素指标空间V中的一个离散的方案点，进行多目标决策，就是比较空间V中各方案点与理想方案点的关联度。则：

很显然，γ01=γ02=……=γ0m=1。

设评价指标间的加权向量为w=（w1，w2，…，w2）T＞0，在加权向量w的作用下构造而成的增广型矩阵为灰色关联决策矩阵F′，且满足：

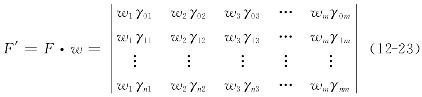
将每个决策方案看成一个行向量，见图12-2，则每个决策方案Ai与理想方案A＊之间的夹角余弦为：

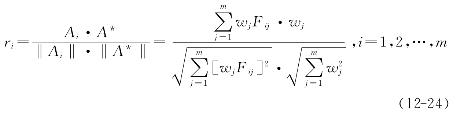
图12-2　灰色关联投影法示意图

很显然，夹角余弦0＜ri＜1，且总是愈大愈好，ri愈大，表示决策方案Ai与理想方案A＊之间的变化方向愈一致。则决策方案Ai的模数di为：

将模的大小与夹角余弦结合考虑，就可全面准确地反映决策方案与理想方案之间接近程度。称决策方案Ai在理想方案A＊上的投影为灰色关联投影值Dj，且满足：

经过上述步骤，就可以得到各比选方案的投影值。根据这些投影值的大小，对多指标的比选方案做出科学的排序比较和分析。