模型六只解决了一个阶段问题，其认为相邻两阶段是独立无联系的，即上一阶段的货物不能在下一阶段销售，如果上一阶段末剩下的货物可以继续在下一阶段出售的话，上述模型就不再适用。

1.需求为离散的随机变量P(r），有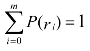。初期剩余存储量I，订货量Q，那么怎样的订货量Q才能使损失期望最

设货物单位成本为K，单位存储费用为C1，本阶段单位缺货费为C2，需求为r，概率为小，即盈利期望最大？

由假设可知初期存储量达到S=I+Q，订货费为KQ。

针对存储费有：

当需求r<I+Q时，剩余货物需支付存储费；当r≥I+Q时，不支付存储费。为了简化，不考虑已售出货物的存储费用，因此存储费的期望为

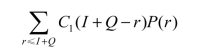
针对缺货费有：

当需求r>I+Q时，(r-I-Q)部分需支付缺货费，所以缺货费的期望为

因此本阶段所有费用的期望之和为

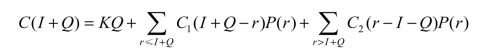
由S=I+Q，上式可以写成

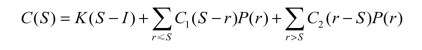
求出S使得C(S)最小。

求解如下：

（1）将需求r的随机值按照从小到大的顺序排列：

r0,r1,…,ri,ri+1,…,rm

可知ri< ri+1，其中i=0,1,…,m-1。

（2）当S取值为ri时，记为Si，则有

ΔSi=Si+1-Si=ri+1-ri(i=0,1,…,m-1)

（3）求S使得C(S)最小，有

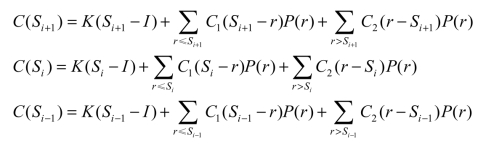
Si最小时应该满足不等式C(Si)≤C(Si +1)，而且C(Si)≤C(Si -1)，那么给如下的定义：

则有

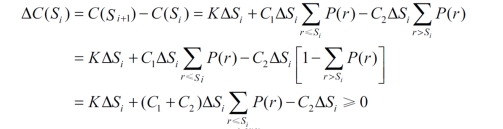
由于ΔSi>0，则有

因此有

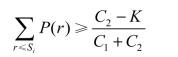(www.daowen.com)

同理可得

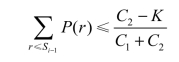
因为(C2－K)/(C1+C2)严格小于1，所以上式又称为临界值，用N表示，即有

N=(C2－K)/(C1+C2)

综合得到Si的不等式：

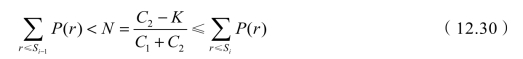
取满足（12.30）的Si为S，即得到最佳存储量，那么本阶段的订货量Q=S-I。

综上所述，此模型的存储策略为，当I≥S时，本阶段不订货；当I<S时，本阶段订货，订货量为Q=S-I，使本阶段存储量达到S时的盈利期望最大。

例12.8　某公司对原料需求如表12.3所示，每箱原料购价K=400元，本阶段存储费为每箱C1=20元，本阶段缺货费为每箱C2=600元，原有存储量I=10箱。

表12.3　原料需求表

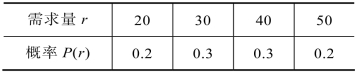
求该公司最佳存储量、最佳订购量以及存储策略。

解 （1）利用公式(12.30)计算临界值：

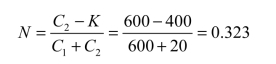
（2）取满足不等式最小的Si作为S，有

P(20)=0.2<0.323,P(20)+P(30)=0.5>0.323

所以最佳存储量S=30箱。

（3）最佳订货量Q=S-I=30-10=20（箱）。

所以初期存储量为30箱，由于原存储量I=10<30，所以需要订购，订购量为20箱。

2.需求为连续的随机变量

设需求r是连续型随机变量，密度函数为f(r)，有，分布函数为，初期存储量为I，其余条件和离散情况一样。

推导从略，不难得出：

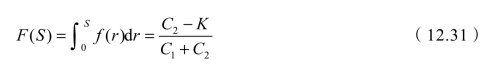
最佳存储量即为S，订货量Q=S－I。

例12.9　某商店销售一种商品，每件进价4元，本阶段每件产品存储费1元，若缺货，每件的缺货费为15元，已知需求量服从[15,20]区间均匀分布，商店目前有8件存货，试求最佳期初存储量和最佳订购量。

解　由题意C1=1，C2=15，K=4，需求概率密度函数为

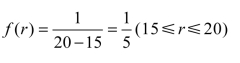
利用公式(12.31)可得

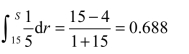
解得S=18.44，取整得到S=19（件），Q=19-8=11（件），即最佳库存量为19件，最佳订购量为11件。