1.需求为离散的随机变量

设货物的单位成本为K，订购费为C3，单位存储费为C1，货物售价为P，滞销的处理价为V，单位缺货费用为C2，订购量为Q，需求量为r，需求量r的概率为P(r)，整个周期只考虑一次进货，试求怎样确定Q使损失期望值最小，即盈利期望值最大。

解　订购量Q与需求量r存在以下三种关系：

（1）供求平衡。即r=Q，滞销损失和缺货损失为0，存储费为。

（2）供过于求。即r<Q，滞销量为Q-r，滞销损失为(Q-r)×(K-V)，缺货损失为0。虽然是一次性进货，但不是一次售完，还应该考虑存储费。假设在一段时间内以不变速率销售完r，那么售出货物的存储费为；滞销的货物在期末一次性处理售完，其存储费为(Q-r)×C1。

（3）供不应求。即r>Q，此时缺货量为r－Q，滞销损失为0，缺货费为(r-Q)×C2。假定在一段时间内以不变速率售完Q，其存储费即为。

损失期望为

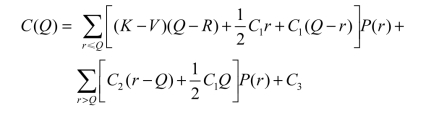
化简为

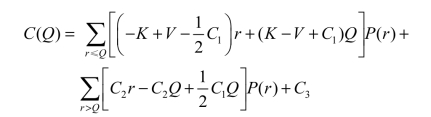
由于r是离散的，不能求导计算最小值，因此采用差分法，最佳订购量应该满足：

（1）C(Q)≤C(Q+1)；

（2）C(Q)≤C(Q－1)。

从（1）式可以得到：

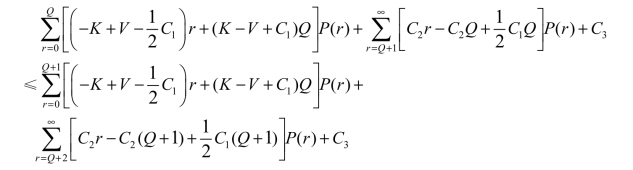
整理得

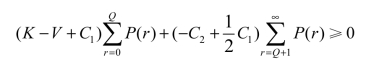
由于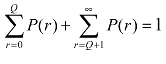，又因为C2=P-K，进一步化简得

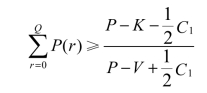
同理，由（2）式可得

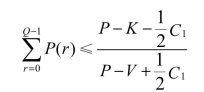
因此最佳订购量Q*应该满足：

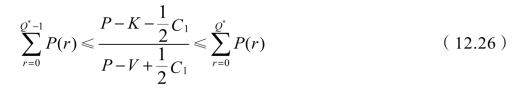
从式（12.26）可以看出，最佳订购量与订购费C3无关。但并不是说按Q*订购就一定会获利，当订购费C3很大时，利润可能为负，按照Q*订购只能使损失最小而已，因此决策时，C3也是个参考的依据。

特别需要说明的是，若存储费用C1=0，那么此时的最佳订购量Q*满足：

这个问题又叫“报童问题”，即假设报童每天售出的报纸数量是一个随机变量，且每售出一份报纸能赚k元，若报纸未能售出，每份赔h元，售出报纸份数r的概率P(r)已知，那么报童每天最好应该准备多少份报纸，此问题根据式（12.27）可以表示为(www.daowen.com)

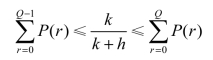
例12.6　某种商品销售旺季为6个月，其需求量的概率分布如表12.1所示，该商品进货价格为每件8元，售价为每件15元，存储费为每月每件0.2元，若滞销，则以每件6元的价格处理完，求最佳的订货量。

表12.1　需求量概率分布表

解　由题意可知，C1=0.2×6=1.2，P=15，K=8，V=6，由公式（11.26）得

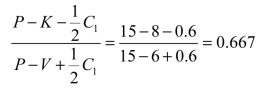
计算结果如表12.2所示：

表12.2　计算结果表

因为0.6<0.667<0.7，所以最佳订购批量应该为140件。

模型六有一个严格约定，即两次订货之间没有联系，是相互独立的，这种存储策略也称为定期定量订货。

2.需求为连续的随机变量

假设条件：需求r是连续的随机变量，密度函数为f(r)，则有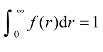，分布函数即为，其余假设条件与离散模型相同。

当订购量为Q时，损失期望为

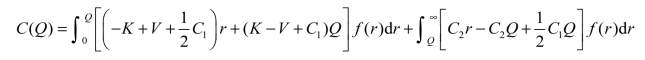
对Q求导，令其等于0，有

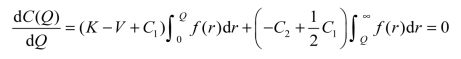
因为及C2=P-K，所以

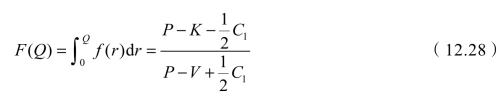
若不考虑存储费，可得

例12.7　某种商品需求呈正态分布，均值μ=150，标准差σ=25。已知商品进价为 6 元，卖价13元，若销售不完可退回原生产单位，每单位按3元处理，求最佳订购批量。

解　由题意可知，P=13，K=6，V=3，r～N(150,252)，则有

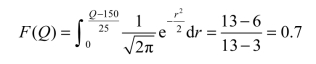
查标准正态分布表可知，使N(0,1)成立的(Q-150)/25值为0.525，因此Q=25×0.525+150=163，即最佳订购批量为163件。