在生产活动的大部分情况下，产品的生产时间是不可忽视的，即生产的批量要有一定的时间才能完成。这类模型和前面所讲的简单经济订货存储模型略有差异，但两者的目的一样，建立模型时，都对模型建立相应的假设条件。

1.不允许缺货，补充需要一定时间的存储模型（模型三）

（1）假设条件。

① 设生产批量为Q，所用时间为t1，则生产速度为P=Q/t1。

② 需求速度为R，应满足P>R。

③ 其他假设与模型一相同。

（2）存储状态图。

存储状态的变化如图12.5所示。

（3）模型建立。

在这种情况下，在t1时间内，每一个单位时间内生产了P件产品，其中提取了R件。也就是说，在区间[0,t1]内，存储以P-R的速度增加；在区间[t1,t]内，存储以R的速度减少，其中t1和t都为待定系数。从图12.5中可以知道，t1时间内产品的生产量等于t时间内产品的需求量，因此有

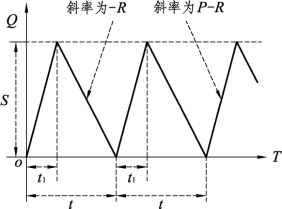
图12.5

(P－R)t1=R(t－t1)

即有 Pt1=Rt

可以求出t1=Rt/P，从而有以下的关系式：

t时间内平均存储量为

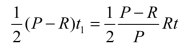
t时间内存储费为

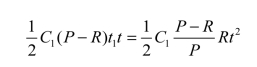
t时间内所需装配费为C3，则单位时间t内总平均费用C(t)的计算公式为

现在需要求出minC(t)，可以采用模型一的求导思路求出最小值，即有

最佳的生产周期t0：

最佳生产批量Q0：

最小总平均总费用C(t0)：

最佳生产时间t1：

最大存储量S0：

很显然，当P趋于无穷大时，P/(P－R)趋于1，同样(P－R)/P也趋于1，因此公式（12.13）、公式（12.14）和公式（12.15）与模型一的三个公式对应相同。

例12.4　已知某厂每月需要甲产品200件，每月的生产速度是600件，每批的生产费是5元，每月每件产品的存储费是0.4元，求最佳的生产周期t0、最佳生产批量Q0、最佳生产时间t1、最小总均总费用C(t0)、最大存储量S0。

解　由题意可得到R=200件/月，P=600件/月，C1=0.4元/月件，C3=5元/批，将值代入对应的公式，计算如下：

最佳的生产周期t0：

最佳生产批量：

最佳生产时间：

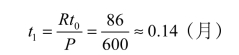
最小总均总费用C(t0)：

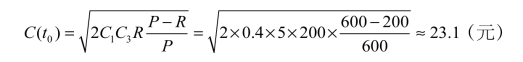
最大存储量：

2.允许缺货，补充需要一定时间的存储模型（模型四）(www.daowen.com)

该模型是以上三种存储模型的综合形式，是既考虑生产速度又考虑允许缺货的情况。

（1）假设条件。

① 生产需要一定时间，生产速度设为P。

② 允许缺货，每单位缺货损失为C2。

③ 其他假设与模型一相同。

（2）存储状态图。

存储状态的变化如图12.6所示。

图12.6

（3）模型建立。

针对图12.6中作如下说明：

取[0,t]为一个周期，设t1时刻开始生产或补充，[0,t2]时间内存储量为0，B为最大缺货量。

[t1,t2]时间内除了满足需求外，还要补足[0,t1]时间内的缺货量。

[t2,t3]时间内除满足必要的需求外，剩余产品入库存储，存储量以（P-R）的速度增加。

S表示存储量，t3时刻达到最大存储量，停止生产。

[t3,t]时间存储量以需求速度R减少，由图12.6可以看出，最大缺货量B=Rt1，或B=(P-R)×(t2-t1)，即有

Rt1=(P-R)×(t2-t1)

从而得到

最大存储量为S=(P-R)×(t3-t2)或S=R×(t-t3)，即(P-R)×(t3-t2)=R×(t-t3)

得到

在内[0,t]时间内所需的存储费为

将公式（12.19）代入上式，消去t3，得到

缺货费即为

将公式（12.18）代入上式，消去t1，化简为

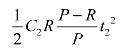
生产装配费为C3，那么[0,t]时间内的平均总费用为

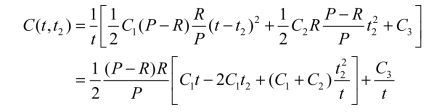
同样采用多元函数求极值办法求C(t,t2)的最小值，令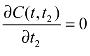，求t的最优值t0及t2，求解过程省略，结果如下：

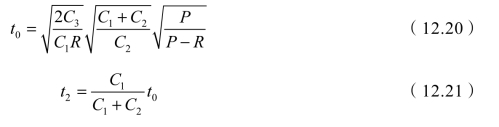
最佳生产批量Q0为

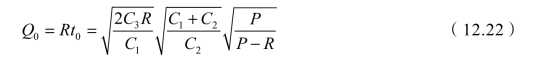
最大存储量S0为

最大缺货量B0为

最小总平均总费用C(t0)为

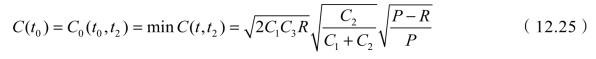
一个存储问题是否允许缺货或补充是否需要时间，取决于实际问题的处理角度，不存在绝对意义的不允许缺货或补充不需要时间。如果缺货引起的后果十分严重，则决策者应采用不允许缺货的建模方式，否则可以视为允许缺货。若补充时间相对于存储周期来说微不足道，则可以考虑建立不需要补充时间的存储模型，否则，视为需要考虑。在考虑补充时间时，需要分清生产时间和提前时间的概念，二者在建模上的处理是不同的。

特别提示

针对确定型存储问题来说，上述四种模型是最基本的模型。其中模型一、二、三可以看做是模型四的特殊情况，因为对于每个模型共有的参数即最优存储周期t来说，式C2/(C1+C2)的有无对应着是否允许缺货，式P/(P－R)的有无对应着补充是否需要时间。