在存储论中，涉及如下几个主要基本概念：

1.需　求

对一个存储系统而言，需求就是输出，即从存储系统中取出一定数量的物资来满足消费的需要，需求的方式可以是间断成批的，也可以是连续均匀的。图12.1和图12.2是两种输出状态，二者在时间t内输出量都为S-W，但图12.1为间断输出，图12.2为连续输出。

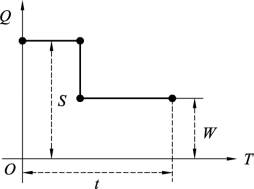
图12.1

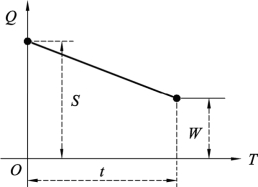
图12.2

单位时间内的需求称为需求量。有些需求量是确定的，比如汽车生产厂商按照订单合同每月卖给消费者多少辆汽车等；有些需求量是随机的，比如书店每月卖出的书可能是1500本，也有可能是800本，对于诸如此类的需求，需要长期统计才能得出每月销售数量的规律。

2.补　充

存储系统由于需求而使存储量不断减少，因此必须加以补充才能满足需求的需要。补充就是存储系统的输入过程，指定周期内订货的数量或生产的数量称为订购量或生产量。补充主要是通过订货和生产来实现，而从订货到货物进入存储状态往往需要一段时间，因此为了在既定时间内能及时得到补充，必须提前订货，这段时间称为提前时间。提前时间可能是确定的，也可能是随机的，当然提前时间可以很长，也可以很短。

3.费　用

费用包含的比较多，其中影响最大的有订货费、生产费、存储费、缺货费。

（1）订货费。

对外采购货物的费用，主要包括两项：一是订货费用，如手续费、交通费、电信往来、人员外出采购的成本等，订货费用是比较固定的费用，与订货的次数有关，但与订货的数量无关；二是货物成本费用，如货物本身的价格、运费等，货物成本费用是可变的费用，与订货的数量有关。

（2）生产费。

补充存储时，不需要对外采购而由本厂自行生产所产生的费用，主要包括两项：一是基本固定的装配费用；二是可变的材料费、人工费等与生产产品数量有关的费用。

（3）存储费。

由于货物占用资金所产生的利息、使用仓库、保管货物以及货物损坏变质造成的损失等费用的总和。这笔费用随着存储量的增加而增加，每件存储物单位时间内所分摊的费用通常用C1表示。(www.daowen.com)

（4）缺货费。

由于存储不足所造成的损失，如供不应求失去销售机会、停工待料等造成的损失，每件短缺物品单位时间内损失的费用常用C2表示。另外，如果不允许缺货，那么缺货费认为是无穷大。

由以上存储费、订货费和缺货费的意义可知，为了保持一定的库存，要付出存储费；为了补充库存，要付出订货费；当存储不足发生缺货时，要付出缺货损失的费用。这三项费用之间是相互矛盾、相互制约的。存储费与所存储物资的数量和时间成正比，如降低存储量，缩短存储周期自然会降低存储费，但缩短存储周期，就要增加订货次数，进而增加订货费支出。为了防止缺货现象的发生，就要增加安全的库存量，但这样在减少缺货损失费的同时，也增大了库存费的开支，因此，要从存储系统总费用最小的前提出发，进行综合分析，从而寻求一个最佳的订购量和补充时机。

4.存储策略

在存储系统中，往往需要把握每次的订购量和补充时机，所以存储论要解决的问题就是多少时间补充一次和每次补充的数量是多少，即指定所谓的最优存储策略。存储策略的优劣取决于该策略所耗费的费用，因此有必要对费用进行分析。

常见的存储策略有三种：

（1）t0循环型策略，即每隔t0时间就补充一个固定的存储量Q。

（2）(s,S)型策略，即经常检查库存量I，当库存量I≥s时，不补充；当I<s时，就进行补充，补充的数量Q=S-I，其中s指最低的库存量，也称订货点、安全存储量或警戒线等，S指最大库存量。

（3）(t,s,S)型混合策略，即每经过时间t检查库存量I，若I≥s时，不补充；若I<s时，使存储量达到S。

无论哪种存储策略，最优存储策略就是既可以使总费用最少，又能避免因缺货而产生的影响。

5.目标函数

要在一些策略中选择一个最优的策略，就需要有一个衡量优劣的标准，即目标函数。在存储问题中，通常把目标函数取为平均费用函数或平均利润函数，选择的策略应该使平均费用达到最小，或者使平均利润达到最大。

综上所述，在确定最优的存储策略时，首先要把实际的问题抽象为数学模型。在形成模型的过程中，对一些复杂的条件要尽量加以简化，只要模型能基本反映实际问题的本质就可以。然后对模型用数学的方法加以研究，从而得出数量的结论，而这些结论是否正确，还要拿到实践中加以检验，如结论与实际不符，就需要对模型重新分析、研究和修改。

存储模型大体上可分为两类：

（1）确定型存储模型，即模型中的数据都是确定的数值。

（2）随机型存储模型，即模型中的数值不是确定的，而是含有随机变量。

下面将按照确定型存储模型和随机型存储模型，分别介绍一些常见的存储模型。