从以上费用模型的讨论可以看出，要根据费用模型得到最优解，关键是正确地估算模型所涉及的有关费用。正如前面所指出的那样，这种估算有时是很困难的，甚至是不可能的，这种情况下，可以考虑用愿望模型来代替费用模型。这里举几个例子予以说明。

例11.17　某车站的一个车场办理接进列车的作业。列车接进后，即可由机车推顶通过驼峰而分解车辆，分解完毕后，该列车离开车场。设列车达到强度平均每小时3列，机车推顶列车可视为列车接受服务，平均服务时间即从推顶开始至整个列车离开车场为15 min，假定服从指数分布。推顶机车仅有一台，车场设有一定数量的股道以停放列车，当股道无空闲时，到达的列车就要暂时被拒绝接入车站。如果管理人员考虑到维持铁路线上列车运行的正常秩序，希望拒绝接车的概率小于10%，那么车场至少应该配备几条股道比较合理？

解　这是一个(M/M/1):(∞/∞/FCFS)排队系统，λ=3，μ=4。设车场设置股道数为m，拒绝接车率为α，则有

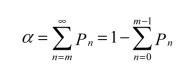
要求α<0.1，即ρm<0.1，得m=9，所以车场至少应配备9条股道。

例11.18　某矿山为保证生产正常运行，要求参加运输的卡车数不少于12辆的概率达到0.97以上，每辆卡车平均连续运输时间为3个月，服从指数分布。有两个修理班负责卡车的修理工作，修理时间服从指数分布，平均修复时间为5天。为满足上述参加运输卡车数的要求，至少应该配备几辆卡车？

解　由问题分析可知，这是一个(M/M/C):(N/N/G)模型，即是多服务员的机器看管问题，r=1/3，μ=6，C=2。可利用式（11.70）以及式（11.71）分别对不同的N（N=13,14,…）计算出在该卡车配备数N的条件下，正在修理或者等待修理的卡车数的概率分布Pn，其中n=0,1,2,…,N-12，并用下式计算参加运输的卡车数Q≥12的概率：

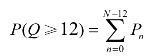
当计算到某个N满足P(Q≥12)>0.97时，即得到所求的卡车配备数量，计算结果如表11.10所示。

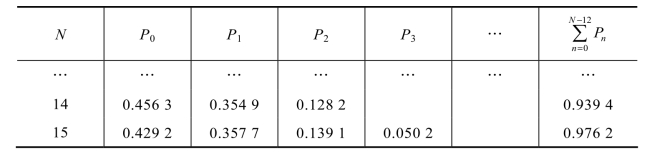
表11.10　计算结果表

(www.daowen.com)

计算结果表明，该矿山至少应该配备15辆卡车。

例11.19　假定有某个(M/M/C):(∞/∞/G)排队系统，λ=10人/h，μ=3人/h。管理人员的愿望就是使得设备空闲率不大于0.4，要求选定C，使一个顾客平均排队等待时间小于5 min。

解　因为设备利用率为λ/(Cμ)，所以第一个目标转化为

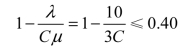
因而有C≤5.56。为了达到第一个目标，必须令C等于或小于5，但为了保证λ/(Cμ)＜1，C必须等于或大于4，所以C只能取4或5。

至于第二个目标，算出各C值条件下的Wq即可。确定C的取值范围，Wq的计算结果如表11.11所示。

表11.11　计算结果表

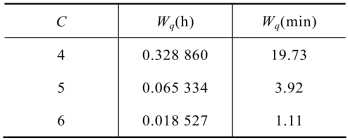
由表11.11可知，5以上的C值只满足第二个目标，5以下的值只满足第一个目标，使两个目标都能满足的唯一C值是5。如果不存在能同时满足这两个要求的C值，则需要修正某个目标。