前面几节介绍了若干排队模型，解决了（当然还没有也不可能完全解决）排队论模型的数学描述问题，但作为一个管理或决策人员，仅仅知道怎样描述排队系统、计算有关运行指标是不够的。研究的真正目的并不在这些，而是要在掌握排队模型的基础上，进一步将它作为决策工具；或者说，当遇到一个实际的排队系统时，而且这个系统的某些参数又有可能改变，例如，服务人员数、服务强度等，那么怎样作出抉择、作出什么样的抉择使系统达到最优，这才是掌握排队系统的最终目的，即所谓的排队系统最优化问题。排队系统的最优化标准，通常是指经济上获得的最大效益。一般而言，减少了顾客在系统中的停留时间，也就减少了停留费用，而这需要提高服务水平，即提高服务强度。还可以通过缩短每个服务员的服务时间或增加服务员的数目来达到这个目的，但这将增加服务机构的成本，所以排队系统最优化的主要目的在于使服务费用和顾客停留费用之和达到最小，图11.3为一个排队系统总费用图。

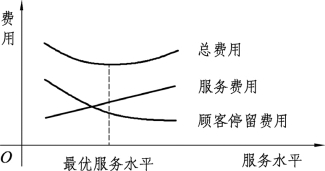
图11.3

服务机构的费用是容易确定的，而顾客的停留费用就不一定能确切知道。例如，若顾客是等待修理的机器，一旦修好即可生产，所以它的停留费用可以计算出来。再如，等待卸货的车辆，减少因排队而产生的停留时间，就相当于增加了用于运输货物的时间，因而其停留费用也比较容易确定。而对于一个企业的排队系统，如果排队的是企业内部的工人，那么可以根据工人的工资或者工人因排队而耽误生产的损失来计算停留损失，如果顾客是企业外部的人，则不好计算其停留费用。停留费用是必须考虑的，如果不考虑这个费用，就有可能为了使总费用最小而降低服务水平。但这意味着排队时间的增加，会导致企业顾客的减少，最终导致利润的减少，这可以看作是一种机会损失费用。所以顾客的停留时间费用必须要以某种方式加以计算，只是我们现在还缺少适用的计算方法，这不能不说是费用模型的一个缺陷。有些时候，可以把机会损失费用作为停留时间的函数进行计算，但是建立这样的函数，需要有足够的统计资料，有的时候，就不得不对停留时间给出最大容许值来确定系统的有关参数。

1.(M/M/1):(∞/∞/FCFS)排队模型的最优µ值（µ值可连续取值）

假定模型的服务强度μ 可以在[λ,∞)的范围内连续变动，显然，μ 越高，服务费用就越高。假定μ 和费用的关系是线性的，例如，如果服务员是由1台或2台甚至是更多的机器联合起来为一个顾客服务，那么μ 与服务费用之间的线性关系是明显的，甚至可以假定增加的机器数为小数（理解这台机器部分时间工作）。当然，在很多情况下，这种假定只是实际情况的近似。

设s为每增大1单位的μ所需要的单位时间服务费用，w为每个顾客在系统中停留单位时间的费用，则系统单位时间期望总费用

c(μ)=sμ+wL

其中，L是系统视为始终保持的顾客数，即系统的期望顾客数。

可以看出，L是μ的函数，那么系统的单位时间顾客停留费用即为wL，根据公式（11.26）有

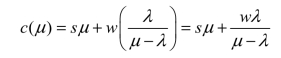
因为μ连续，为了求极小值，先求出导数，令它等于零，则有

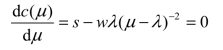
因为μ>λ，μ-λ应该取正值，则有

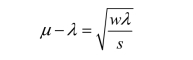
从而最优的μ值为

2.单服务员模型的最优μ值（μ是离散的）

上述关于μ 可以连续取值的假定往往与实际不符，所以现在讨论μ 有m个离散值的情形，此时不能用求导的方法求最优值。这里介绍另一种方法，即假定可能的服务强度从小到大依次为μ1,μ2,…,μm。这类模型分3种情况考虑：

（1）为了提供μi，所需费用为sμi。

（2）提供μi的费用是μi的非线性函数s(μi)，对一切i有

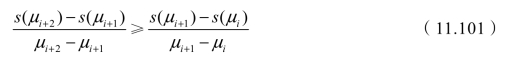
式（11.101）表明，随着μi的增大，费用的增长速度会越来越快。

（3）提供μi的费用为s(μi)，但s(μi)不具备式（11.101）所具有的特点。

如果是情况（1），则 s(μi)=sμi。这种情况和 μ 连续取值的模型类似，所以可以按照如下步骤求最优：

（1）按前面介绍的方法求出μ*；

（2）如果第一步求出的μ*存在于可能的μi序列中，则μ*就是最优解，否则转入下面的第（3）步。

（3）在可能的μi序列中找出μi*值两边的两个μi，最优解一定是其中一个。可以证明，顾客停留费用wL是凸函数。又因为sμi是线性的，所以各项费用之和是凸函数，因此可以断言，最优μi就是两个当中费用较小的一个。

如果是情况（2），总费用也是凸函数，式（11.101）成立。这意味着对于任何 i，点(μi+2,s(μi+2))和点(μi+1,s(μi+1))连线的斜率大于点(μi+1,s(μi+1))和点(μi,s(μi))连线的斜率，因而用直线将相邻点连起来的曲线是凸的。再考虑其他费用，也是凸函数，所以总费用就是凸函数。

例11.11　假定有 6 台机器能用来提供某项服务，这些机器类型、服务强度及每小时费用见表11.3。这是一个(M/M/1):(∞/∞/FCFS)排队系统，w=8元/h，λ=5/h，要求找出最优μ。

表11.3　机器类型、服务强度及每小时费用表

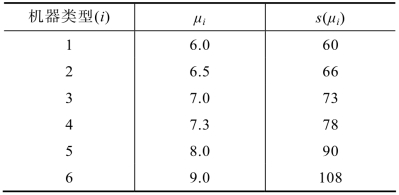
解　计算每一种μi下的总费用，以寻找最优μi，这当然是可以的，但在μi的可能值较多时就比较麻烦。由于表11.3中的数据能满足式(11.101)，因而费用是凸函数。现在从最小的μi计算费用，一旦发现某一个c(μi+1)大于c(μi)，就停止计算，并得到μ*=μi。表11.4列出了计算出的所有μi值。

表11.4　计算结果表

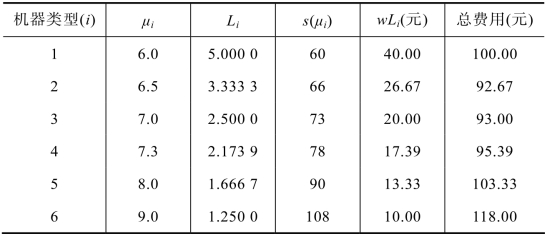
实际上，计算出c(μ3)时就可以停止计算，因为c(μ3)>c(μ2)，并得到最优服务强度μ*=μ2=6.5。

至于第（3）种情况，因为不满足式(11.101)，总费用不是凸函数，所以就需要对每一个μi计算总费用，才能找出最优的μ。

3.多服务员模型最优C值

以(M/M/C):(∞/∞/G)排队模型为例来进行讨论。模型中，G表示排队规则不限。在多服务员模型中，服务员数目一般是一个可控因素，增加服务员会提高服务水平，但也会增加与它相关联的费用。假定这个费用是线性的，即与服务员的数目成正比，设h为提供一个服务员每单位时间的费用，则对于(M/M/C):(∞/∞/G)排队模型来说，费用函数即为其中，C是离散的，并且在任何情况下必须有(λ/Cμ)<1，即必须有C>λ/μ。

为了求出最优的C，可以计算每个可行C值的总费用，费用最小者为C*，即最优的C，或者当C的可行值很多时，可以利用下面的关系式找出最优的C：

在确定C*时，如果上面两式成为充分条件，式(11.102)就必须是凸函数，即构成费用函数的各点必须是一凸集的顶点。因为式(11.102)的第一项是线性的，此外还能证明L是C的凸函数，wL也是C的凸函数，因而式(11.102)是凸函数。

如果式(11.103)对最优解一定成立，则有

式中，L{C*}表示按照C*求出的L值。上式整理后为

按照式（11.104）即可求出C*。

例11.12　某公司要确定其实验室的最优实验设备套数，已知平均每天来做实验的有48人，服从泊松分布，每个实验人的损失费用w=12，实验时间服从指数分布，平均服务强度为25人/天，提供一套实验设备的费用合计为每天5元。试决定该公司配置的最优实验设备套数。

解　这是一个(M/M/C):(∞/∞/G)排队模型，λ=48，μ=25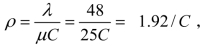，，为了使ρ<1，就应该有C>1。

根据式(11.42)有

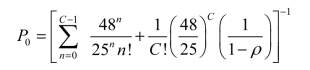
再根据式(11.43)和式(11.46)有

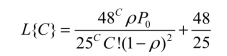
对不同的C值分别计算L{C}，结果如表11.5所示。(www.daowen.com)

表11.5　计算结果表

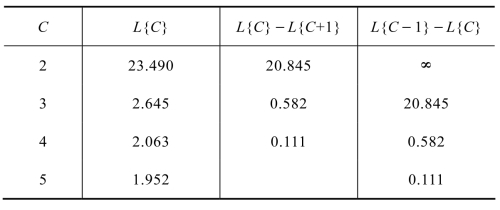
因为h/w=5/12=0.417，根据式(11.104)和表11.5，可配置最优的实验设备套数C*=4。

4.多服务员模型最优C、μ 值

仍以(M/M/C):(∞/∞/G)排队模型为例进行讨论。

（1）μ 的费用是线性的。

假定C和μ 都是离散的，所有服务员具有相同的服务强度μ，s的定义同前，则提供服务的总费用为Csμ，其中C和μ 都是变量。如果设L{C}为使用C个服务员的队长，那么费用函数为

式(11.105)中有两个变量，需要对其求最优值。

先令μ保持不变，按照前面讲述的方法求最优C，然后改变μ值。用同样的方法再求最优C，这样一直做下去，直至所有的μ都考虑到，即可得到这个模型的最优C。

（2）μ的费用为非线性函数。

如果设s{μ,C}为提供C个服务员的费用，每个服务员的服务强度为μ，那么总费用函数就为

在这种情况下，一般需对全部μ和C的组合逐个进行计算，才能求得最优的μ和C。下面对服务费用是一个特殊非线性情况进行讨论：

设有m种机器可以选来作为服务设备，其服务强度分别为μ1,μ2,…,μm。提供服务的费用包括两部分，即机器购置费和机器运转费用。令 vi表示第i种机器运转一个单位时间的费用，假定仅当机器运转即为顾客服务时才有这个费用，可以理解为燃料或电能的消耗等。为了计算平均运转费用，需要知道服务设备的时间利用系数，不难证明，总服务能力的利用系数为λ/Cμ。如果令Ci表示第i种服务设备的选定数目，则Ci个设备实际运转一个单位时间的费用为viCi，再乘以利用系数即为平均运转费用：

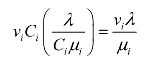
可见单位时间的运转费用是μ的非线性函数。若令hi表示得到一个第i种服务设备的单位时间费用，令L{Ci}表示采用Ci个第i种服务设备时的队长，则本模型费用为

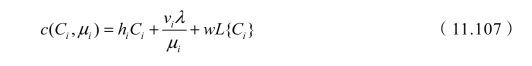
一般情况下，μ 和C的数目有限，费用最低的μ 和C的组合是能够找到的。

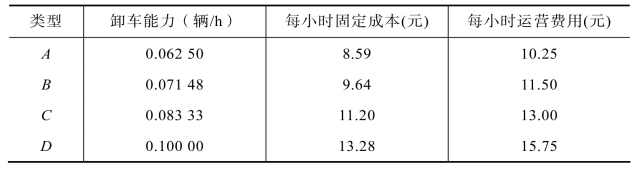
例11.13　某车站正在计划配备卸车机械，市场上有4种类型可供选择，有关资料如表11.6所示。可配备1台、2台或3台机械。多于1台时，要求为同一型号，卸货车辆的到达为泊松分布，平均每小时到达0.07143辆，卸车时间服从指数分布，车辆每小时停留费用为20元。要求决定选用何种类型的机械和设置台数。

表11.6　卸车机械资料

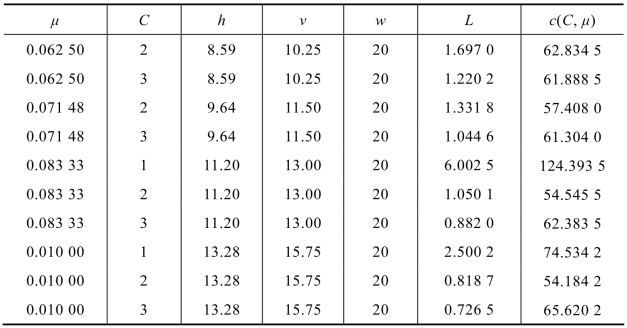
解　这是一个(M/M/C):(∞/∞/FCFS)排队模型，要求同时决定最优μ和C。可以利用式（11.107）对不同μ和C的组合进行计算。需要注意的是，任何情况下，都应保证C>λ/μ，计算结果见表11.7。由表中c(C,μ)栏数字可知，μ*=0.10000，C*=2，即最优方案是选用D型机械2台。

表11.7　计算结果表

5.费用模型其他示例

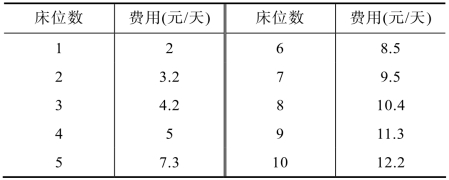
例11.14　某小旅馆要确定合适的床位数，旅客平均每天到4人，服从泊松分布，每个旅客平均住宿1天，服从指数分布。旅客到达时如发现床位已满就离去，旅馆床位数最多为10个，旅客住宿1天，旅馆获利5元。提供不同床位的每天费用如表11.8所示，那么该旅馆应该设置多少床位最好。

表11.8　旅馆床位费用表

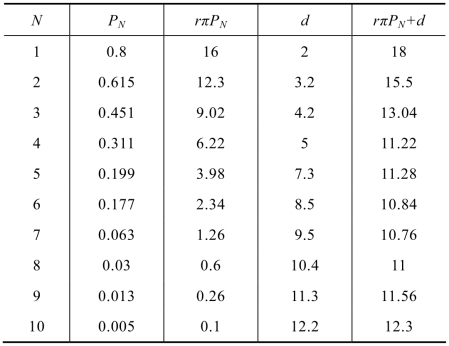
解　这是一个多服务员、系统容量有限的模型，服务员数与最大容许顾客相等，是(M/M/N):(N/∞/G)模型。希望进入系统的到达强度r=4/天，服务强度μ=1/天，拒绝1个旅客损失π=5元。利用式(11.56)和式(11.57)计算，单位时间总费用包括拒绝旅客的损失费用rπPN和提供床位的费用d。计算结果如表11.9所示，由该表可知，最优床位数是7。

表11.9　计算结果表

例11.15　某工厂生产一项产品，其加工的某些工序有两种方案：若采用设备A，平均加工时间为4 min，服从指数分布，设备费用为每小时2元；若采用设备B，加工时间为5 min，设备费用为每小时1.8元。产品以每小时8件的速率到达这一工序，产品在加工过程中每延误1 h，对工厂将有3元的损失，应该选择哪一种设备更合理。

解　对两个方案分别分析。

（1）采用设备A。

这是一个(M/M/C):(∞/∞/G)排队系统，λ=8，μ=15，L=λ/(μ-λ)=1.143，

总费用=设备费用+产品停留损失=2+3L=5.429

（2）采用设备B。

这是一个(M/D/1):(∞/∞/G)排队系统，λ=8，μ=12，

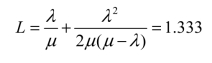
那么总费用为1.8+3L=5.799。

因为设备A的费用低于设备B的费用，所以选用设备A。

例11.16　某商店出售一种昂贵商品，单位时间的需求量为λ，服从泊松分布。每当有一个需求时，商店就向生产此商品的工厂定一个货，工厂的加工时间服从指数分布，参数为μ，显然这将出现有需求而无货的情况。设缺一个货的单位时间损失为h元，为了减少这种缺货状况，商店拟存放m个产品以作调剂，但库存量也不宜过多，因为存储也有费用。设单位产品存放单位时间的费用为e元，问题是如何确定库存容量m，才使单位时间期望总费用c(m)最小？

解　如果把生产商品的工厂看作服务机构，订货（即需求）的发生看作顾客的达到，则构成一个(M/M/1):(∞/∞/FCFS)排队系统，Pn表示在稳定状态下，工厂有n个订货未交出的概率。

平均缺货数为

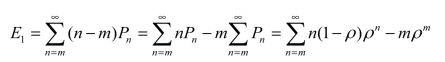
平均存货数为

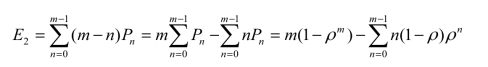
将E1、E2两式代入总费用的计算式有

最终得

据此，可求出使得c(m)达到最小的m值。