(M/M/C):(∞/∞/FCFS)排队模型和(M/M/1):(∞/∞/FCFS)排队模型在结构上的区别是服务员的个数为C个，即C>1。特点是一个服务员在同一时间只为一个顾客服务，当顾客到达后，如果有空闲服务员，就立刻接受服务，否则参加排队。但无论排队的队列形式如何，在服务时的队列只有一个队列。服务员在服务结束后，如果队列中有等待的顾客，就按照先到先服务的原则为下一个顾客服务，其中每个服务员的服务时间都服从均值为1/μ的指数分布。

以上关于(M/M/C):(∞/∞/FCFS)排队模型的特点描述十分重要，不具备这些特点中的任何一个特点，都不是(M/M/C):(∞/∞/FCFS)排队模型。假如顾客是在每个服务员前形成一个单独的排队队列，并且服务员只为对应队列中的顾客提供服务，那么就不是所谓的(M/M/C):(∞/∞/FCFS)排队模型，而是C个(M/M/1):(∞/∞/FCFS)排队模型。

根据(M/M/C):(∞/∞/FCFS)排队模型的特点可知，当顾客数n小于C时，系统的服务强度为nμ，当顾客数n大于等于C个时，系统的服务强度应该为Cμ，即有

基于泊松分布的可加性，系统的服务强度无论是nμ还是Cμ，其仍然服从泊松分布，即可以利用生灭过程的稳态结果来研究本模型的相关运行指标。

1.(M/M/C):(∞/∞/FCFS)排队模型的相关指标

（1）状态概率分布Pn

根据式（11.11）有

上式的分母分别为

因而有

根据式（11.12）有

对于多个服务员模型，服务员的繁忙度应该为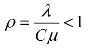，则有

所以

（2）排队长Lq

当系统有n+C个顾客时，有C个在接受服务，有n个顾客在排队等待，所以

最终有

（3）顾客平均等待时间Wq

把公式（11.43）代入Little公式有

（4）顾客平均停留时间W

基于公式（11.34）和公式（11.44）有

（5）队长L

基于Little公式和公式（11.28）有

需要说明的是，可以把(M/M/1):(∞/∞/FCFS)排队模型看作(M/M/C): (∞/∞/FCFS)排队模型的特例，即当(M/M/C):(∞/∞/FCFS)排队模型的C=1时即为(M/M/1):(∞/∞/FCFS)排队模型。另外，C=∞时，即为(M/M/∞):(∞/∞/FCFS)排队模型。这是一个典型的服务员为无穷多的系统，相当于每个顾客都是随到随服务，所以系统始终不会出现排队现象。利用(M/M/C):(∞/∞/FCFS)排队模型的相关公式，不难得到(M/M/∞):(∞/∞/FCFS)排队模型的相关公式。

特别提示

在(M/M/C):(∞/∞/FCFS)排队系统中，因为服务员数量为C个，所以当系统内顾客数n<C时，新到顾客不需要排队，当系统内顾客数n≥C时，新到顾客就需要排队等待。

2.(M/M/C):(∞/∞/FCFS)排队模型的示例

下面基于例11.1售票排队问题，对(M/M/C):(∞/∞/FCFS)排队模型的相关运行指标进行具体计算。(www.daowen.com)

例11.2　在例11.1的基础上，考虑为了减少购票乘客排队等待的时间，现增设一个售票窗口，即多增加一个售票员。售票员给一个乘客的平均售票时间仍然为2 min，服务时间服从指数分布，现在计算此排队系统的有关运行指标。

解　购票乘客平均到达强度λ=20人/h，售票员平均服务强度μ=30人/h，服务员数目C=2，那么服务员的繁忙度ρ=λ/(Cμ)=20/(2×30)=1/3。

相关运行指标如下：

（1）售票厅内没有购票乘客的概率P0：

说明购票乘客到达售票厅后，没有购票乘客即不需要排队的可能性是50%。

（2）排队长Lq：

说明此排队系统期望排队的购票乘客数为0.083人。

（3）购票乘客平均等待时间Wq：

说明购票乘客的平均等待时间为0.25 min。

（4）购票乘客平均停留时间W：

说明购票乘客的平均停留时间为2.25 min。（5）队长L：

说明此排队系统期望的购票乘客数为0.75人。

（6）购票乘客到达后系统内有4个以上购票乘客的概率P(n>4)。

首先计算出P1、P2、P3、P4，再计算P(n>4)，基于公式（11.41）有：

n=1时，有

n=2,3,4时，分别有

那么有

说明购票乘客到达售票厅后，售票厅内有4个以上购票乘客的概率为0.62%。

（7）购票乘客不排队的概率P(n≤1)。

购票乘客到达后不排队，说明售票厅内要么没有购票乘客，要么只有一个购票乘客，据此可计算购票乘客无需排队的概率P(n≤1)。基于公式（11.41）有

说明购票乘客到达售票厅后，马上能购票的可能性是83.3%，购票乘客不得不排队购票的可能性是16.7%。

现在假设将两个售票窗口分设在两个不同的地点，并假设每个地点的到达强度为原来到达强度的一半，即10人/h，仍然服从泊松分布，在这种情况下，我们不难计算出它的队长以及购票乘客的平均停留时间：

这种情况下购票乘客平均停留时间要比两个售票窗口集中设置时大，可见尽管都是设置了两个售票窗口，但采用不同的排队模型，效果就不一样。采用集中使用的方案优于采用分散使用方案（当然包括形式上在一起，实际上是分散使用的方案），这种现象在经济学中称为“规模效益”，所以在考虑服务设施的布局与使用时，需要考虑这一原则。

另外，通过例11.1和例11.2，从排队的角度看，这个铁路售票厅采用(M/M/2):(∞/∞/FCFS)排队模型比采用两个(M/M/1):(∞/∞/FCFS)排队模型要优一些，但铁路售票部门需要增加售票员，这也增加了成本。所以针对一个排队系统，评价它的优劣不能只从顾客角度或服务机构角度来单一考虑，至于如何使排队系统最优，在后面章节的排队论在决策中的应用中再分析。