(M/M/1):(∞/∞/FCFS)排队模型中顾客到达间隔时间为泊松分布，服务时间为指数分布，系统容量和顾客来源无限，先到先服务，只有一个服务员，即C=1。设顾客到达强度为λ，服务员服务强度为μ。

1.(M/M/1):(∞/∞/FCFS)排队模型的相关指标

（1）状态概率分布Pn

利用公式（11.11）和公式（11.12），先计算系统状态的概率分布。由前面的分析有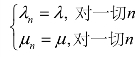。设ρ=λ/μ表示服务员的繁忙时间，也称为繁忙度，即意味着服务设施的利用系数，于是有

到达强度λ 必须小于服务强度μ，否则系统排队长度将会越来越大，以至出现“爆炸”现象，此时就不是排队问题了，因此有0<ρ<1。

根据几何级数求和公式有

将上式代入公式（11.21）得

将公式（11.23）代入式（11.20）得

（2）队长L

队长L是指系统期望的顾客数，结合公式（11.24）有

利用繁忙度公式，还有

（3）排队长Lq

排队长Lq是指系统期望排队的顾客数，结合公式（11.25）有

将公式（11.23）代入式（11.27），有

将公式（11.26）代入式（11.28），并利用繁忙度公式，则有

公式（11.28）也说明了排队长和队长的关系。

（4）顾客平均停留时间W

顾客平均停留时间W是指顾客在系统内期望的停留时间，有

利用公式（11.26）有

（5）顾客平均等待时间Wq

顾客平均等待时间Wq是指顾客在系统内期望的等待时间，有

利用公式（11.29）有

公式（11.30）和公式（11.32）称为Little公式。

将公式（11.28）代入公式（11.32），并利用繁忙度公式，则有

公式（11.34）也说明了顾客平均等待时间Wq和顾客平均停留时间W的关系。

通过上述这些公式可以看出，由到达强度λ和服务强度μ就可求出这些指标值。

（6）停留时间的概率分布

设T表示系统中第n+1个顾客停留时间的随机变量，既然T是第n+1个顾客的停留时间，也就是当顾客到达时系统已经有n个顾客，所以停留时间T的密度函数fT(t)应该是条件密度函数f(t|n)，其中t表示T的具体值。不难理解，第n+1个顾客在系统内停留的时间等于已在系统内的n个顾客停留时间的总和再加上自身的服务时间。当第n+1个顾客到达时，若n≠0，那么总有一个顾客正在接受服务，并已服务了一段时间，根据指数分布的无记忆性，这个正在接受服务的顾客的剩余服务时间和其他还在等待的顾客的服务时间一样，也服从同样的指数分布。所以完成n+1个顾客的服务所需时间T的概率分布恰好是n+1阶爱尔朗分布，参数为1/μ和n+1，其条件密度函数为

T和N的联合密度函数应等于条件概率密度函数f(t|n)和N的概率分布PN(n)（或者记为Pn）的乘积：

根据公式（11.24）有

T的概率密度等于fT,N(t,n)，对所有n的总和为

因为，所以

可见fT (t)是指数分布，参数为1/μ(1-ρ)，据此可以求出期望停留时间W：

可以看出，关于期望停留时间W的公式（11.36）和公式（11.31）是一致的。(www.daowen.com)

（7）顾客到达后必须等待k个以上顾客的概率P(n>k)

利用概率论知识，顾客到达后必须等待k个以上顾客的概率为

如果利用此公式求必须等待k个以上顾客的概率P(n>k)，当k较大时，计算量较大。如果利用公式（11.23）和（11.24），可得概率P(n>k)的更简明公式：

（8）顾客停留时间超过给定时间t的概率P(T>t)

根据顾客停留时间T的密度函数公式（11.35），可得到T的累积分布函数：

那么T大于t的概率为

2.(M/M/1):(∞/∞/FCFS)排队模型的示例

下面用售票排队问题，对(M/M/1):(∞/∞/FCFS)排队模型相关运行指标进行计算。

例11.1　某铁路售票厅，假设有一个售票窗口，经过统计和分析可知，在一天的高峰期内，购票乘客平均每小时到达20名，购票乘客的到达服从泊松分布。售票员给一个乘客的售票时间平均为2 min，售票时间服从指数分布。计算此排队系统的有关运行指标。

解　由题可知，购票乘客平均到达强度λ=20人/h，售票员平均服务强度μ=30人/h，那么服务员的繁忙度ρ=λ/μ=20/30=2/3。

相关运行指标如下：

（1）队长L：

说明此排队系统期望的购票乘客数为2人。

（2）排队长Lq：

说明此排队系统期望排队的乘客数为1.33人。

（3）购票乘客平均停留时间W：

说明购票乘客的平均停留时间为6 min。

（4）购票乘客平均等待时间Wq：

说明购票乘客的平均等待时间为4 min。

（5）购票乘客不排队的概率P0。

只有当购票乘客到达时，恰好售票厅内也没有购票的乘客，到达的购票乘客才能不必排队而立即购票，则

说明购票乘客到达售票厅后马上能购票的可能性是33%，那么购票乘客不得不排队购票的可能性就是67%。

（6）购票乘客到达后必须等待4个以上购票乘客的概率P(n>4)。

先利用公式（11.37）计算P(n>4)：

则有

前面在公式（11.37）处已经提到，当k较大时，计算量较大，这里如果假设计算购票乘客到达后必须等待15个以上购票乘客的概率，计算起来会很麻烦，所以利用公式（11.38）计算P(n>4)：

说明购票乘客到达售票厅后，售票厅内有4个以上购票乘客的概率为13.2%。

（7）购票乘客停留时间超过12分钟，即0.2 h的概率P(T >0.2)。

利用公式（11.40）可得

说明购票乘客停留时间超过12 min的可能性是13.5%。

由前面知道，购票乘客期望的平均停留时间为6 min，超过6 min的可能性是

这就是说，购票乘客在本购票排队系统中，停留时间超过平均停留时间6 min的概率是36.8%，那么小于平均停留时间6 min的概率就是63.2%。