1.生灭过程

（1）生灭过程定义。

设有某种生物构成的一个群体，最初由i个细菌组成，随着时间的推移，由于细菌的增生，一个分裂为两个，也有细菌的死亡，那么经过一段时间之后，细菌的数量就会发生变化。这是一个典型的生灭过程的例子，不少排队过程和这个生灭过程有相仿之处。

设某个系统，具有状态集S={0,1,2,…,i}或S={0,1,2,…}，令N(t)表示系统在时刻t(t≥0)所处的状态，如果系统的状态随时间t变化的过程满足下述条件，则称这一变化过程为生灭过程。

设在时刻t，系统状态处于n的情况，在经过足够短的时间Δt内：

① 系统状态由n转移到n+1的概率为λn(Δt)。

② 系统状态由n转移到n-1的概率为μn(Δt)。

③ 系统状态由n转移到其他状态，即增加一个以上或减少一个以上，总的概率为可以忽略不计的高阶无穷小o(Δt)。

由以上定义可知，如果把状态的变化理解为排队系统顾客的到达和离去，那么在足够短的时间增量δ (t)内，只会有一个到达，或者只有一个离去，或者既无到达也无离去。出现既无到达也无离去情况的概率为1-λn(Δt)-μn(Δt)-o(Δt)。另外，到达一个或离去一个的概率与Δt的长短有关，而和起始时刻t无关，即和系统的运行时间无关；到达一个或离去一个的概率还和系统时刻t的状态n有关，即λn是n的函数，而和以前的状态即状态的演变过程无关。

把过程状态变化的这个特性称为马尔可夫性质，把具有生灭过程特征的排队模型称为马氏过程排队模型。

下面分两种情况推导系统状态概率分布的微分方程：在时刻(t+Δt)时状态n=0的概率、在时刻(t+Δt)时状态n≠0的概率。

① 在时刻(t+Δt)时状态n=0的概率。

时刻t的状态和Δt时间内发生的事件组合，需要使时刻(t+△t)时的状态n=0，即表格11.1所列的情况：

在表11.1中，因为n=0时Δt内不会有顾客离去，所以μ0(Δt)=0。根据全概率公式有

表11.1　时刻(t+Δt)时状态n=0的情况

式中，o(Δt)与一个未知概率相乘，得到的仍然是可以略而不计的o(Δt)。将式（11.1）两边减去P0(t)，再除以Δt，然后取Δt趋于0的极限，于是有

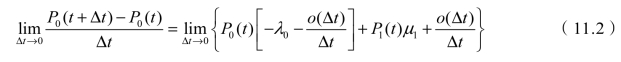
显然，式（11.2）定义了P0(t)关于时间的导数，则有

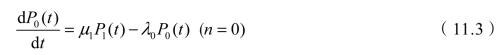
② 在时刻(t+Δt)时状态n≠0的概率。

时刻t的状态和Δt时间内发生的事件组合，需要使时刻(t+Δt)时的状态n≠0，即表格11.2所列的情况：

表11.2　时刻(t+Δt)时状态n≠0的情况

同样根据全概率公式有：

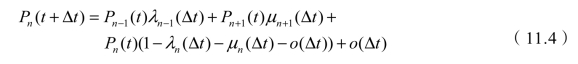
式中，o(Δt)与一个未知概率相乘，得到的仍然是可以略而不计的o(Δt)，将式（11.4）两边减去Pn(t)，再除以Δt，然后取Δt趋于0的极限，于是有

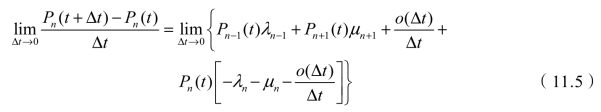
显然，式（11.5）定义了Pn(t)关于时间的导数，则有

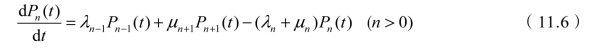
（2）生灭过程的稳态解。

根据两个关于时间的导数方程（11.3）和（11.6），可以求出系统初始状态为n、运行时间t以后达到各种状态的概率分布情况，即瞬态解。

针对瞬态解的两个方程求解相当复杂，而且也不便于应用，所以需要找出稳态解，即系统运行的时间t充分大时所得到的解。此时，系统状态的概率分布已经不再随着时间的变化而变化，基本达到统计上的平衡。也就是说，系统在运行充分长的时间以后，在任意一个时刻，系统状态n的概率为常数。

需要指出的是，虽然在理论上系统需要经过无限长的时间才会进入稳态，但在实际中，一般总是很快就会达到稳态，所以计算系统在稳态下的一些运行指标，如队长L、排队长Lq、顾客期望停留时间W、顾客期望等待时间Wq等，基本能反应系统的正常情况。

既然在稳态状况下概率分布Pn(t)与时间t无关，那么Pn(t)关于时间的变化率应该等于零，所以对于一切n有。因为稳态和时间无关，所以可以将符号简化，用Pn代替Pn(t)，于是方程（11.3）和（11.6）变换为

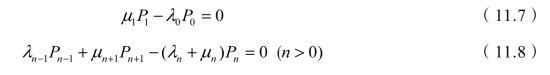
对公式（11.8）进行整理，有

令gn=μnPn－λn－1Pn－1，再结合公式（11.7），即有gn=gn－1=…=0，其中n>0，所以有

从有

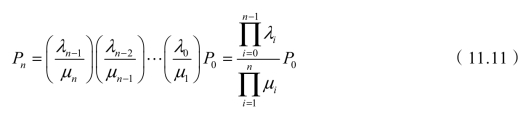
现在把P0的计算式推导出来。当状态为无限集时，有

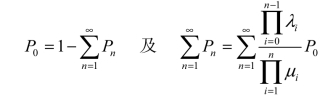
于是有(www.daowen.com)

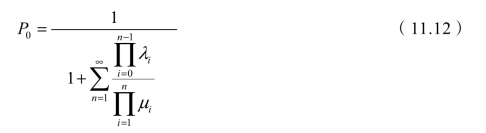
当状态集为有限集，即S＝{1,2,…,k}时，有

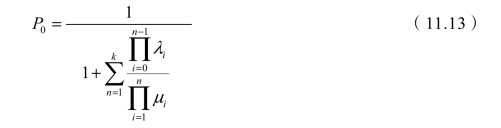
公式（11.11）、（11.12）和（11.13）给出了稳态下系统的概率分布。

2.泊松分布

对于到达过程的随机性，可以换一个等价方式来表述，即在给定的时间内，系统到达顾客数（随机变量）服从泊松分布。下面对这一问题进行讨论。

用N(t)表示系统在时间区间[0,t)内到达的顾客数，Pn(t)表示在时间t内到达n个顾客的概率，遵从以下三个性质的分布过程称为泊松分布过程。

（1）平稳性。

在时间t内平均到达的顾客数只与时间t的长短有关，而与时间的起点无关。

（2）无后效性。

在时间t内到达n个顾客这一事件，与起始时刻以前发生的事件是相互独立、互不关联的。

（3）普通性。

在充分小的时间间隔中，最多有一个到达发生，有两个或两个以上到达的概率很小，以至可以忽略。

根据以上性质，可以推导泊松分布的形式。这里把输入过程作为一个没有离去的排队过程来分析。假设系统的初始状态为零，将t分为m个区间。当m充分大时，基于普通性的性质，在区间t/m内，最多只有一个到达发生，那么在区间t/m内平均到达的个数即为λt/m；基于平稳性的性质，λ为常数，因此平均到达个数λt/m可以作为区间t/m内发生一个到达的概率。现在把到达过程设想为做m次独立试验，若在t/m内有一个到达发生，则试验成功，若无到达，则试验失败。基于无后效性的性质，每次试验成功的概率都是λt/m，那么在时间t内成功n次(n≤m)的概率，即在时间t内有n个顾客到达或经过时间t系统内有n个顾客的概率为二项分布：

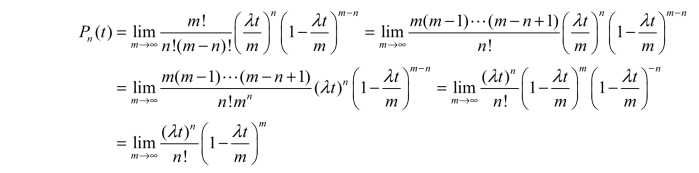
因为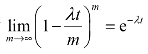，所以有

公式（11.14）就是参数为λt的泊松分布。

可以证明，上述泊松分布的期望值，也就是在时间t内到达顾客数的平均值，即E(N(t))=λt，方差V(N(t))=λt。现在很容易理解常数λ 的物理意义了，即λ 表示顾客平均到达强度。

特别提示

对于其他形式的到达分布，不能一概地认为在任意一个时间间隔t内，平均到达的顾客数一定等于λt。

3.指数分布

设T表示从一个顾客至下一个顾客到达的时间间隔，由公式（11.14）可知，在时间t内，系统到达顾客数为0的概率为P0(t)＝e-λt 。T小于等于t的概率P(T≤t)用F(t)表示，则有

概率P(T≤t)也称为T的累积分布函数。根据此函数，可以求出T的密度函数：

这就是参数为1/λ的指数分布，1/λ也是平均到达的时间间隔，即有E(T)=1/λ。因此，对于可以用参数λt描述的泊松分布的输入过程，也可以用参数1/λ 的指数分布来描述。反之亦然，这就是泊松输入过程与到达时间间隔服从指数分布的等价性，对此结论不做证明。

指数分布有以下两个主要特性：

（1）无记忆性。

例如，顾客到达时间间隔服从指数分布，平均时间为8 min。如果在某一任意时刻考察这个到达过程，发现最后一个顾客已到达了 5 min，那么下一个顾客平均还需要8 min，似乎已过去的5 min被忘却，所以称“无记忆性”。

下面证明这一特性。

令R表示任一时刻，利用公式（11.16），可以求出T大于等于R的概率：

那么T大于等于R和T大于等于R+h的联合概率就等于T大于等于R+h(h≥0)的概率：

给定T≥R，则T≥R+h的条件概率为

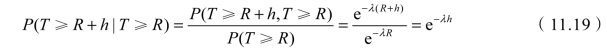
这个条件概率和R无关。也就是说，无论在什么时刻，考察至下一个顾客到达所经过的时间，其概率分布即P(T≥R+h|T≥R)与此刻之前的最后一个顾客是什么时候到达无关，它和顾客相继到达间隔的时间都服从参数为1/λ的指数分布。

（2）可加性。

设{N1(t),t≥0}和{N2(t),t≥0}是两个相互独立的泊松输入过程，平均到达强度分别为λ1和λ2，则{N1(t)+N2(t),t≥0}仍然是一个泊松输入过程，其平均到达强度为各平均到达强度之和，即λ=λ1+λ2。

以上讨论了服从泊松分布的输入过程，依据指数分布和泊松分布等价性，这些讨论显然对于具有指数分布服务时间的服务过程也是有意义的，因此不必再讨论服务机构。

泊松到达和指数服务的服务员的排队模型显然是一个生灭过程，因为泊松分布的特性恰好满足了生灭过程的几个条件。但这个模型显然是一个特殊情况下的生灭过程，即对所有n，有λn=λ、μn=μ，即系统具有不变的到达强度λ 和服务强度μ。对于其他具有泊松到达和指数服务的模型，例如，多服务员模型、系统容量有限模型等，可以根据已介绍的有关泊松分布特性进行判断，它们都是某种特殊情况下的生灭过程，这可以利用已得到的生灭过程结果，方便地求得各个模型的一些有用的运行指标。

下面依次对以下排队模型进行介绍：

针对其他的马尔可夫排队模型，如(M/M/1):(∞/N/FCFS)、(M/M/C):(∞/N/FCFS)、(M/M/1):(∞/∞/LCFS)、(M/M/C):(∞/∞/SIRO)等，本书不予介绍。