前面介绍的统筹问题，都是根据给出的详细资料，如劳动分配资料、投资资料等等，得出明确的工序一览表，从而绘制统筹图，再基于统筹图来解决问题。也就是说，到目前为止，统筹图中各工序的工序时间，是根据已有的资料，或者对以往的历史数据进行分析，最终确定的已知数，即统筹图中所考虑的工序时间都是确定的，把这类问题称为确定型统筹问题。 针对现有的工程项目，如果由于资料不完备等原因，可能会造成工序时间不确定；针对一个未来的项目，许多工序的时间没有什么可供参考的资料，这时工序时间也就不能是确定的已知数；另外，在实际的工程项目中，各道工序的实际劳动生产率常常是一个变动的量，它要受人力、物力、财力等各种因素的影响，因此每道工序的工序时间都会出现随机性，这时就产生了不确定性问题，把这类问题称为非确定型统筹问题。

为了编制进度计划和绘制统筹图，需要把非确定型统筹问题转化为确定型统筹问题，这样就用前面所讲的方法来编制工程进度计划和绘制统筹图，即所谓的计划评审技术（PERT）。计划评审技术（PERT）和关键路线法（CPM）都是工程计划编制和管理的有效工具，所不同的是处理方式和解题技巧有所差别。

用计划评审技术（PERT）解决非确定型统筹问题，首先必须确定全部工序的工序时间。对于非确定型问题的工序时间，需要相关的技术人员、管理者等估计最可能时间、乐观时间和悲观时间。

所谓最可能时间，就是在正常情况下，完成该工序所需要的时间，一般用m表示；所谓乐观时间，就是在一切都顺利的情况下，完成该工序所需要的最短时间，一般用a表示；所谓悲观时间，就是在最坏的情况下，完成该工序所需要的最长时间，一般用b表示，但悲观时间的估计，不考虑像地震、火灾、洪水、战争或其他非常少见的大灾等特殊情况。上面这种方法称为“三时估计法”。

在PERT方法中，对工序时间的“三时估计法”，就是将上述三种时间的加权平均数作为完成该工序时所需的估计时间，用te(i,j)表示，计算公式为

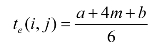
针对某项工程，如果对各道工序作了三时估计，将估计值te(i,j)作为期望值，当做实际的工序时间看待，可绘出统筹图，这样就可以把非确定型统筹问题当做确定型统筹问题来处理，从而找出关键路线。

由于工序时间的不确定性，使工序时间成为一个随机变量，不过乐观时间a和悲观时间b这两个估计值发生的概率较小，而最可能时间m发生的概率较大。可以设想，工序时间这个随机变量服从一个单峰分布，也有许多人认为，工序时间是服从单峰点在m、端点在a和b之间的β分布，如图10.22所示。在图10.22中，te(i,j)即为工序时间的估计值，其实也为期望的近似值。设端点a、b均在距离期望值的6个标准差σ(i,j)之内，即有6σ(i,j)=b-a，因此工序(i,j)的工序时间的方差可以近似为

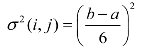
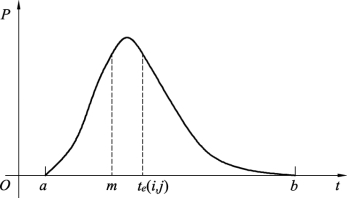
图10.22

在关键路线法（CPM）中，整个工程的完工期TE是由关键路线中所有关键工序的工序时间之和得出的，但这里的工序时间都是随机变量，因此工程完工期TE也是随机变量，也存在期望值E(TE)与方差D(TE)。

因为定义的工序是相互独立的，所以工程完工期TE的期望值E(TE)就等于关键路线中所有关键工序的工序时间的期望值总和，整个工程的完工期TE的方差就等于关键路线中所有关键工序的工序时间的方差总和，即有

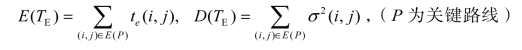
其实，事项的最早时间tE(j)也是一个随机变量，同样也有方差和标准差。为了方便计算，在统筹图的标识上，和确定型统筹问题不同，即把确定型统筹图中的工序时间，用te(i,j)和σ2(i,j)的分数形式标识，分子表示te(i,j)，分母表示σ2(i,j)。另外，把确定型统筹图中方框“□”内的事项最早时间的标识，用期望的事项最早时间EtE( j) 和方差D( j) 以分子分母的形式替代。事项最迟时间tL( j) 的标识不变，即仍标识在节点右下角的三角框内，如图10.23所示。

图10.23

针对非确定型统筹问题，当关键路线不止一条时，取其中方差最大的作为关键路线。那么现在的问题就是，在求得的期望完工期内，整个工程完成的可能性即完成的概率究竟有多大，根据中心极限定理，大量的随机变量相加而成的随机变量服从正态分布。而针对非确定型统筹问题，整个工程的完工时间是由关键路线中各道关键工序的期望完成时间相加而成，而工序的期望完成时间又是相互独立的随机变量，因此当工序足够多时，工程完工期TE近似地服从均值为E(TE)和方差为D(TE)的正态分布，如图10.24所示。

由概率论知识可知，工程在期望完工期内完工的概率可由概率分布曲线下的面积积分求得，所以可利用标准正态分布的数值表查找；对于服从非标准正态分布的随机变量，标准化后，可利用标准正态分布的数值表求算，因为完工期TE是服从非标准正态分布的，所以需要标准化，设新的随机变量为X，则

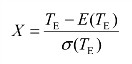
X服从标准正态分布，即X～N(0,1)，则有

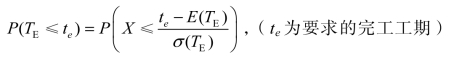
这样就可以根据规定的工期和标准正态分布表，计算出整个工程在要求的完工工期内完成的概率。

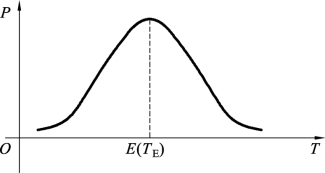
图10.24(www.daowen.com)

需要指出的是，计划评审技术（PERT）中的工序完成时间是随机变量，即在工程实施过程中，工序完成时间有可能出现各种不同的值，那么统筹图的关键路线也会随之发生变化。因此，工程技术人员和管理人员等需要随着工程的进展，根据实际完工的情况，不断的调整或更新统筹图的网络计划，从而使整个工程始终不偏离最有效地利用各种资源、使工程总费用最低的预定的目标。

下列通过一个例题，对非确定型统筹问题进行具体的说明。

例10.6　某项工程的工序关系以及三时估计值如表10.8所示。

（1）试求该工程的E(TE)、D(TE)和标准差σ (TE)。

（2）如果该工程的完工期TE服从正态分布，那么要求该工程在49天之内完成的概率是多少？

（3）如果该工程的完工期TE服从正态分布，那么要求该工程在44天之内完成的概率是多少？

解　利用前面的相关公式，计算出工序时间的估计值te(i,j)及工序时间的方差σ2(i,j)，并列于表10.8的右边。根据表10.8，绘制统筹图，并计算事项参数，如图10.25所示。

表10.8　例题10.6的数据表

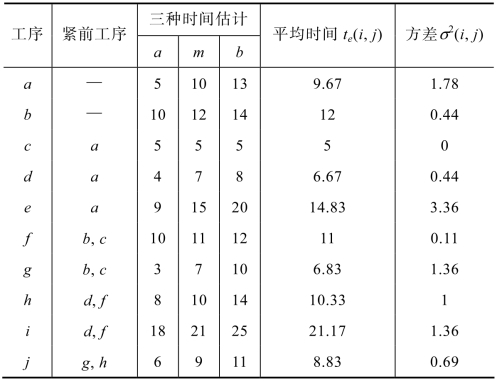
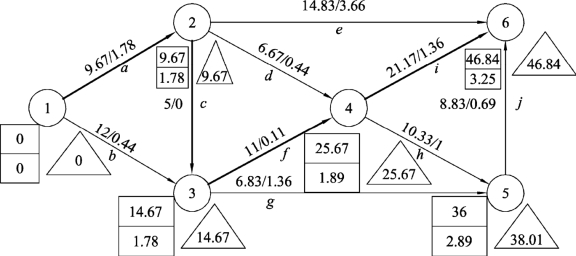
图10.25

（1）根据计算出的时间参数，确定的关键工序是a、c、f、i，由关键工序的工序时间的期望值，求出工程完工期的期望值：

E(TE)=te(1,2)+te(2,3)+te(3,4)+te(4,6)=9.67+5+11+21.17=46.84(天)

工程完工期的方差为

D(TE)=σ2(1,2)+σ2(2,3)+σ2(3,4)+σ2(4,6)=1.78+0+0.11+1.36=3.25

工程完工期的标准差为

（2）如果此工程的完工期TE服从正态分布，则由上面的概率公式得

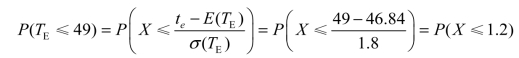
根据标准正态分布表P(TE≤1.2)=0.88，可知此工程在49天之内完成的概率是88%。

（3）再由上面的概率公式得

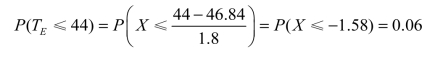
即此工程在44天之内完成的概率是6%，说明在44天内完工的可能性很小。