在前面的章节中，通过时间参数的方法，求出了统筹图的关键工序和关键路线，目的是保证工程按期或提前完成。而这个思路是只考虑时间而制定工程计划，即针对一项工程只考虑工期进度最优。但在制定工程计划时，不仅要把时间进度最优作为目标，有时还要考虑其他的目标最优。

编制统筹图计划的目标大体上有：

（1）在费用限制下完工时间最少；

（2）在完工时间限制下费用最少；

（3）完工时间及费用均最少。

针对一项工程，采取一定的组织措施，安排合理、调度得当就可以保证工程按期完成。如果为了使特定的工序或整个工程提前完成，就需要通过改进技术或改善管理等措施，来缩短相应的工序时间。这些措施和方法主要有：

（1）利用非关键工序的人力、物力和财力，去协助关键工序，通过这样的协作缩短关键工序的作业时间。

（2）可以调整统筹图的网络结构，改变工序之间的关联关系。

（3）作业方式上采用平行作业或交叉作业的方法，以缩短工期。

（4）优先给关键工序提供所需的条件。

（5）缩短最经济的关键工序。

为了使特定工序或整个工程提前完成，需要采取一定的措施和手段，而这些都可能增加一定的费用。如果提前完成产生的收益超过所增加的费用，采取的措施和手段还是划算的，尽管如此，还需要考虑哪些工序需要采取措施缩短工时、工时又缩短多少。

这一节将针对工程费用和时间一起考虑时，制定最少工程费用的方案。

任何一项工程的总费用基本是由直接费用和间接费用两大类组成。

直接费用是与完成工序有直接关系的费用，如人力、机械、原材料等费用。在一定条件和一定范围内，工序的作业时间越短，直接费用就越多，所以缩短工序的作业时间，会增加直接费用。

间接费用是指完成工序所产生的管理费、设备租金等等。间接费用是根据各道工序的工序时间来分配的，由此可知，工序时间越少，间接费用就越低，反之，工序时间越多，间接费用就越高。因此缩短工序的作业时间，加快工程进度，可以节省管理费、设备租金等间接费用。

工程费用与完工时间之间的关系，可用图10.17描绘。缩短工期的最低限度称为最短工期，即赶工时间。从图10.17中可以看出，在正常工期和最短工期之间，存在一个最优的工期，此时总费用最少，那么目标就是要找出总费用最少和最优的工期，即最低成本工期。从关键路线入手，找出总费用最少的最优工期就是关键路线法(CPM)。

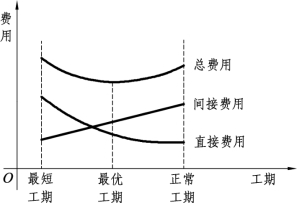
图10.17

一般来说，间接费用与工期近似呈正比关系，而直接费用与工期的关系则是一种反比关系，但这种关系只在一定范围内存在。为了方便起见，可以近似假设直接费用与工期也呈线性关系，如图10.18所示。

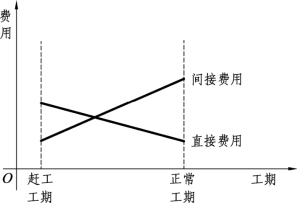
图10.18

设工序k每赶工一天所需要增加的费用为w(k)，则其费用斜率的计算公式为

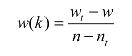
式中，w(k)为费用斜率，wt为赶工所需费用，w为正常完工所需费用，n为正常完工所需时间，nt为赶工时间。

显然，费用斜率越大的工序，每缩短一单位的时间，所花的费用就会越高。在考虑缩短工程的工期时，当然是要缩短关键工序中的某一道或几道工序的工序时间，而究竟选择缩短哪道工序的工序时间，要以总费用最省为原则，所以应当选择关键工序中费用斜率最低的那道工序，从而使总费用最少。

正常完工时，总费用是直接费用与间接费用的总和，即

W＝U+V

式中，W为总费用，U为直接费用，V为间接费用。

赶工完工时，总费用变为

式中，W为总费用，U为直接费用，（wt-w）为赶工增加的费用，V为间接费用。(www.daowen.com)

下列通过一个例题，对最少工程费用方案的制订问题加以说明。

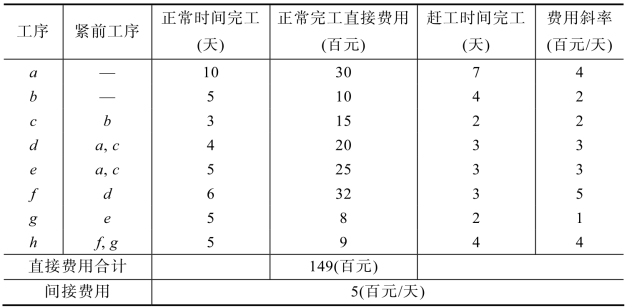
例10.5　根据某项工程的有关资料，分析出的有关工序信息、相应的费用、时间以及费用斜率见表10.6，试制定该工程最少工程费用的计划方案。

表10.6　例题10.5相关数据表

解　根据表10.6，绘制统筹图并计算事项参数，结果如图10.19所示。

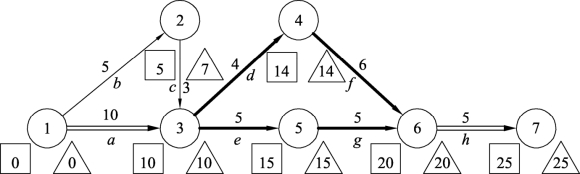
图10.19

可知关键路线的路长为25，即按正常时间完工的工期是25天，所需要的总费用W=14900+500×25=27400元。

如果使工程工期最短，可先将所有工序的工序时间都压缩到赶工时的完工时间，统筹图如图10.20所示。

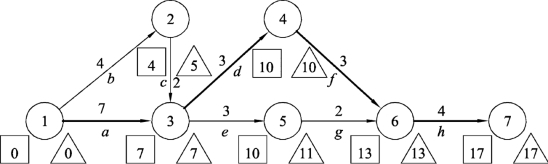
图10.20

可知赶工的关键路线的路长为17，即赶工时的完工工期是17天，此时赶工增加的费用(wt-w)为3×400+1×200+1×200+1×300+2×300+3×500+3×100+1×400=4700元，那么所需要的总费用W=U+(wt-w)+V=14900+4700+500×17=28100元。

赶工节省了8天，但总费用也很高，这就需要寻找更优一点的方案。

下面分析如果按照正常时间完工，最少工程费用方案如何确定。由图10.19可以看出，在按正常时间完工的统筹图中，有两条关键路线，第一条是a、d、f、h，第二条是a、e、g、h，其中工序a、h为两条关键路线所共有。另外，两条关键路线在事项3和事项6之间有并联的关键工序，如果要缩短工期，就需要缩短关键工序的时间，所以在上述有两条关键路线的情况下，首先考虑缩短共有的关键工序。

在此先考虑缩短关键工序h。工序h每缩短1天，就增加费用400元，但节省的间接费用为500元，所以会有100元的净节省费用。因此，可以把工序h压缩到赶工时间的最低限度4天，那么总费用变为W=27400-100=27300元。

现在再考虑缩短关键工序a。与压缩工序h一样，每压缩1天，同样有100元的净节省费用，但此时需注意，工序a不能压缩到赶工时间的最低限度7天。因为当工序a压缩2天时，工序时间就变为8天，如果再压缩，原来的非关键路线就变成了关键路线，这样工序b和工序c就变成了关键工序。在事项1和事项3之间，也出现了并联的关键工序，所以若继续单独压缩工序a，已经不能缩短整个工程的工期，因此，只能把工序a的工序时间压缩到8天，所需要的总费用变为W=27300-(100×2)=27100元。

现在，还需要继续压缩工期。在还可以压缩的关键工序中，可以进行如下考虑：

如果将工序a和工序b各缩短1天，虽然可以达到缩短工期的要求，但使费用增加600元，大于间接费用节省的500元，总费用反而增加，这样就不符合要求。同理，同时压缩工序a和工序c，总费用也会增加。

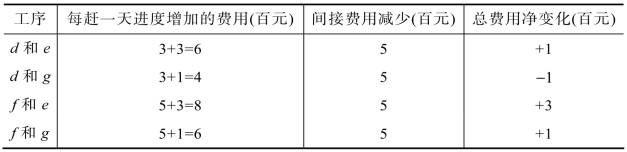
再来考虑事项3和事项6之间的各关键工序d、e、f和g。根据它们之间的并联情况，要想缩短工程的工期，必须在工序d、f中和工序e、g中各压缩一道工序的时间，这样，就会出现下列4种可能的组合，如表10.7所示。

从表10.7中可见，除了压缩工序d和g的组合能使总费用减少外，如果压缩其他三组，均会使总费用增加，因此，将工序d和工序g各压缩1天，所需要的总费用变为W=27100-100=27000元，由于工序d的限制，不能再进一步压缩了。

表10.7　压缩工序的4种可能组合

综合起来，此例题的最少工程费计划方案，应该按照下列方式进行：

将工序a压缩为8天，将工序d压缩为3天，将工序g压缩为4天，将工序h压缩为4天，其他工序b、c、e和f仍按照正常时间进行，这样得到工程的工期为21天，总费用为27000元，其最终的统筹图如图10.21所示。

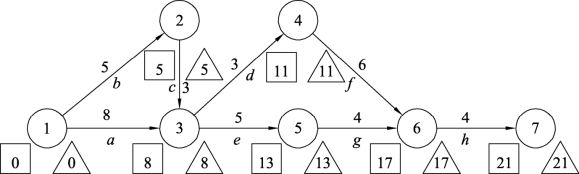
图10.21

以上所介绍的这种找最少工程费用方案的方法，其实是全枚举法。这种方法只适用小型工程项目，而对于庞大的工程项目，就会包含许多并联的关键工序，而每一条路线又含有大量的工序，如果再利用全枚举法，就需要检查并联线路中一切可能的工序组合，这样做会使工作量很庞大。例如，有两条关键路线，其中并联部分各有20道工序，那么必须将400种工序组合逐个进行检查，所以，针对大型工程，需要采用数学规划等其他方法。

还需要指出的是，在编制工程进度计划时，除考虑时间和费用以外，有时还需要考虑合理安排人力、物力等有限的资源。尤其在资源较为紧张时，要合理调配，以保证急需的关键工序正常进行，必要时甚至要适当推迟工程的完工时间。这些都需要计划人员或工程管理人员等进行宏观控制，根据实际情况灵活掌握。

特别提示

从已了解的统筹方法可知，统筹图优化的思路、方法、分析等贯穿于统筹图的绘制、调整以及执行的全过程。