将工程任务分解为若干道工序，并按照规则绘制出统筹图以后，就应当确定完成整个工程所需的最少时间，而这个最少时间是由对整个工程影响最大、所需时间最长、从始点事项至终点事项的一连串工序决定。这就是掌握工程完工的关键所在，同时，可以对整个工程的工序进行控制，以便使工程能够按期完工。另外，还可以通过控制某些工序的开工时间，或者是通过改进工艺、提高管理措施等手段，使某些工序的工序时间缩短，从而使整个工程提前完工。

1.相关概念

为了达到以上目的，下面依次给出相关概念。

在统筹图中，从始点事项出发，经过一组按同一方向依次连接的箭线（有向边）和事项（节点）到达终点事项的路线称为路；一条路中各道工序的工序时间总和称为该路的路长；统筹图中路长最大的路称为关键路线，或称为主要矛盾线；关键路线上的工序称为关键工序；其他工序称为非关键工序。

例10.3　图10.10是某项工程的统筹图。

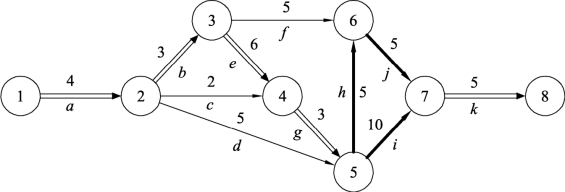
图10.10

下面用全枚举法列出图10.10的所有路，共7条：

第1条路：①→②→③→⑥→⑦→⑧，路长L1=4+3+5+5+5=22。

第2条路：①→②→③→④→⑤→⑥→⑦→⑧，路长L2=4+3+6+3+5+5+5=31。

第3条路：①→②→③→④→⑤→⑦→⑧，路长L3=4+3+6+3+10+5=31。

第4条路：①→②→④→⑤→⑥→⑦→⑧，路长L4=4+2+3+5+5+5=24。

第5条路：①→②→④→⑤→⑦→⑧，路长L5=4+2+3+10+5=24。

第6条路：①→②→⑤→⑥→⑦→⑧，路长L6=4+5+5+5+5=24。(www.daowen.com)

第7条路：①→②→⑤→⑦→⑧，路长L7=4+5+10+5=24。

通过比较可知，第2条与第3条的路长最大，所以第2条与第3条均为关键路线，路长为31，即该工程的工期为31天。关键工序为a、b、e、g、h、i、j、k，其中工序a、b、e、g、k为第2条与第3条关键路线的共有关键工序。另外，该统筹图有两条关键路线，这意味着统筹图中，关键路线可能不止一条。

绘制统筹图的目的就是全面掌握和控制工程的进度。在统筹图中，关键路线一般用粗线、双线或颜色线标示出来，关键路线的路长即为整个工程的工期。如果某任意一道关键工序超期完成，将会导致整个工程延期，所以要保证关键工序按时或提前完成，这样才能保证整个工程按期或提前完工。

2.相关性质

基于前面的相关概念以及对例题10.3的了解，给出如下的性质：

（1）非关键路线上非关键工序的时间缩短，不会使整个工期提前，因为关键路线并没有发生变化；当非关键路线上非关键工序的时间延长时，如果没有使非关键路线的路长超过关键路线的路长，就不会影响整个工期；如果使非关键路线的路长超过了关键路线的路长，就会造成整个工程延期，同时关键路线也发生了变化。

（2）当关键路线只有一条时，只要有关键工序的工序时间发生变化，就会影响整个工期，即任意一道或几道关键工序超期完成，都会造成整个工程延期；反之，只要有关键工序提前完成，就会使整个工程提前完工。

（3）当关键路线只有一条时，如果关键工序的工序时间缩短，那么关键路线的路长也会随之缩短。当路长仍然不小于任意一条非关键路线的路长时，关键路线没有变化，但整个工程会提前完工；当路长小于任意一条非关键路线的路长时，那么原来的关键路线就变成了非关键路线，而原来某一条或几条非关键路线就成为关键路线，当然关键工序随之发生变化，同时整个工程也会提前完工。

（4）当关键路线不止一条时，只有共有的关键工序的工序时间缩短，才会使整个工程提前完工；另外，任意一个关键工序超期，都会造成整个工程延期。

（5）当关键路线不止一条时，非共有的关键工序的工序时间缩短，不会使整个工程提前完工，但关键路线少了一条或几条；非共有的关键工序的工序时间延长，关键路线就发生变化，并造成整个工程延期。

特别提示

（1）上述性质也说明，在统筹图中关键路线是相对的。

（2）另外还有其他性质。比如，尽管缩短非关键工序的时间不会使整个工期提前，但并不是说缩短非关键工序的时间没有意义，因为缩短非关键工序的时间，可以直接或间接的节省相应的资源，或者可以将节省下来的时间做其他利用。