前面介绍的网络流问题，在分配调整流量时，都要遵循容量约束条件和流量守恒条件，而且给出的网络图容量也是确定的，但在实际问题中，往往需要突破容量约束条件或流量守恒条件。另外，有的实际问题恰恰需要对网络的输送能力进行改善，即对容量进行提高，以满足流量不断增加的需要。解决这些问题有一定的现实意义。

下面简单介绍两方面的网络扩展应用问题，从而拓展解决现实问题的思路。

1.转运点有流量需求的最大流问题

针对网络图的最大流分配问题，常用的Ford-Fulkerson算法等都是在容量约束条件和流量守恒条件下，将顶点分为源、汇及中间点三类。其中，中间点只具有转运作用而没有流量需求，然后基于寻找增流链的方法，使流量的分配达到最大化。但在实际的运输网络应用中，转运顶点往往有流量需求，这类问题可以说是普遍存在，那么这类的转运顶点就不能简单地按照源、汇或中间点来归类。有流量需求的顶点具有中间点的转运属性，但不遵循流量守恒条件，而Ford-Fulkerson算法是在容量约束条件和流量守恒条件下进行最大流分配的，Ford-Fulkerson算法不能对此问题分配最大流，所以单纯使用传统的算法就不能够很好地解决这类最大流分配问题。

下面针对转运顶点有流量需求的情况，在基于Ford-Fulkerson算法基础上，介绍一种转运顶点有流量需求的最大流分配算法，从而为解决实际运输网络应用问题提供基础。

假设运输网络G的顶点vi需求流量为Z，算法的基本思路如下：

（1）基于运输网络G，按照如下方法构建新的网络图G′：G中顶点vi以外的点和边在G′中保持原来的状态；将G中顶点vi在G′中一分为二，拆分为vi和vi′两个顶点，顶点vi作为中间点角色转运流量；顶点vi′作为汇角色接收需求的流量Z；G′中的顶点vi和G中的顶点vi保持同样的连接状态；G中以顶点vi为终点的边，在G′中仍然与顶点vi′连接，G中以顶点vi为起点的边，在G′中不再与顶点vi′连接，最后把网络图G′化为单源单汇的网络图。

（2）在G′中，利用标号法思路寻找包含顶点vi′的增流链，再按照最大流算法，把顶点vi′接收的流量之和调整到需求的流量Z。

（3）为了保证运输网络G满足容量约束条件，把G′中以顶点vi为终点的边(vj,vi)的容量c(vj,vi)修改为新的容量c′(vj,vi)，即c′(vj,vi)=c(vj,vi)-f(vj,vi′)。

（4）在G′中，利用标号法思路寻找不包含顶点vi′的增流链，再按照最大流算法，进行最大流分配。

（5）按照上面步骤对G′分配完最大流以后，再将vi和vi′两个顶点合二为一即可。

下面通过示例，介绍转运点有流量需求的最小费用最大流问题。

例9.29　某运输网络如图 9.140所示，图中边的数据表示容量和零流，要求在满足顶点v6需求流量为5的条件下，对该运输网络分配最大流。

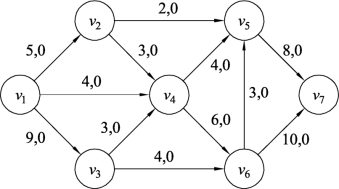
图9.140

解 （1）将图 9.140 顶点 v6拆成 v6 和 v6′，并化为单源单汇网络，如图9.141所示。

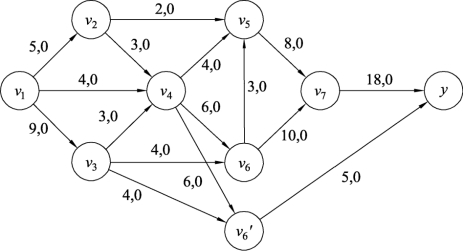
图9.141

（2）在图9.141中，利用标号法思路寻找包含顶点v6′的增流链，再按照最大流算法，把顶点v6′接收的流量之和调整到需求的流量5，结果如图9.142所示。

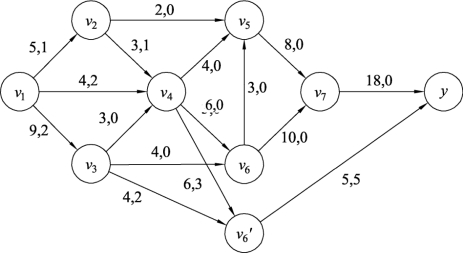
图9.142(www.daowen.com)

（3）为了保证图9.140满足容量约束条件，需要把图9.142中以顶点v6为终点的边的容量均修改为新的容量，结果如图9.143所示。

（4）在图9.143中，利用标号法思路寻找不包含顶点v6′的增流链，再按照最大流算法，进行最大流分配，反复进行，最终结果如图9.144所示。

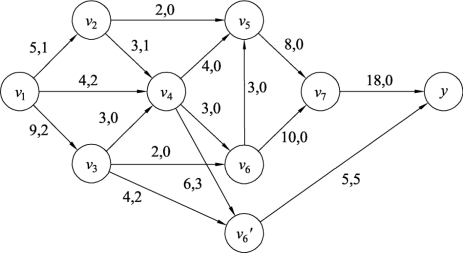
图9.143

（5）图9.144中尽管还存在增流链，但包含了顶点v6′，所以流量调整结束，将顶点v6和v6′合二为一，则顶点v6需求流量为5的最大流如图9.145所示。

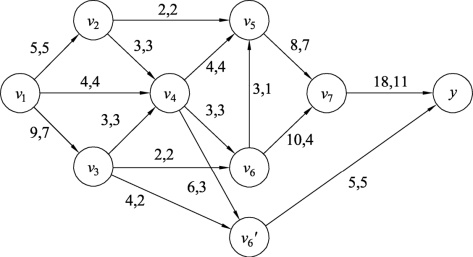
图9.144

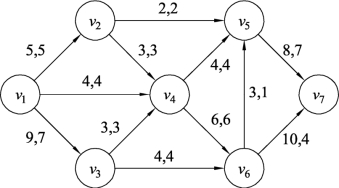
图9.145

特别提示

上述示例只给出了一个顶点有流量需求的处理方法，对多个顶点有流量需求时，这种算法仍然可以对多个顶点一分为二，在此基础上进行流量分配即可。

2.网络的扩能问题

前面介绍的网络流应用中，都是基于容量是确定的，但在网络图的实际应用中，随着时间的推移，流量的发展态势往往超出网络图的最大输送能力，这就需要考虑如何提高网络的输送能力，以满足流量发展态势的需要，这就是网络的扩能问题。网络扩能在现实中普遍存在，如道路网、水网、信息网等改建扩建问题就是网络扩能。

针对整个网络的扩能，有时既要考虑流量的发展态势，又要考虑网络扩能的代价，同时还需要考虑网络流的均衡问题，所以网络扩能问题是相当复杂的问题。鉴于网络扩能的复杂性，这里不给出相应的算法，只给出一个以供扩展思路的简单例题的描述。

例9.30　有一个网络图如图9.146所示，图中边的数据表示容量和流量。已知该网络的流量状态已经达到最大流，最大流流值为21，根据预测可知，在一定的预测期内，网络流量的流值可能达到30。鉴于目前的网络能力和未来流量的发展态势，需要对该网络进行扩能，已知各个边的单位扩能成本如表9.14所示，试设计最优的扩能方案。

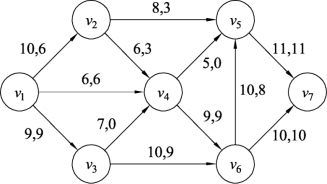
图9.146

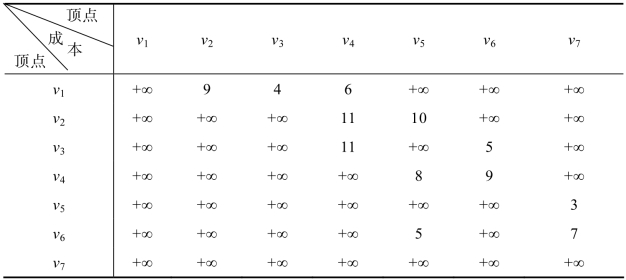
表9.14　各边的单位扩能成本