有关流量分配的算法是，在遵从容量约束条件和流量守恒条件下，只追求流量的分配，这样势必造成以下两个问题：

（1）过于理论化，即算法在理论上合理，但不一定符合实际现象。假设网络图9.122表示城市交通路网，利用理论算法分配的最大流如图中所示，但是实际路网中车流量的分布状态并不一定和图所示的理论分配相一致。

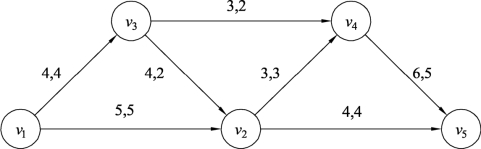
图9.122

（2）只考虑流量量值大小的调整，而不考虑网络中流向的分布状态，这样就有可能造成网络流的分布不均衡，即有些边的流量过于接近容量而趋于饱和，有些边的流量很小，造成边的利用率很低。仍然假设网络图 9.123 表示城市交通路网，利用理论算法分配的最大流如图中所示，而边(v3,v4)的流量为0，没有被利用。另外，边(v2,v4)和边(v2,v5)相比，边(v2,v4)的利用率偏低，而边(v2,v5)过于饱和。

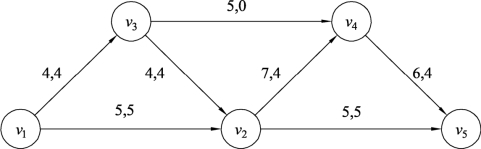
图9.123

鉴于既要考虑流量量值大小的调整，又要考虑网络中流量的分布状态即流的流向，也就产生了网络图流量均衡分配的研究。

另外，最大流算法、最小费用流算法以及最小费用最大流算法在调整分配流量时，只要满足容量约束条件和流量守恒条件即可。但现实中的一些具体问题，往往会对流量的分配有其他的条件要求，这种情况下，再单纯地使用这些算法，就不能够很好地解决有其他条件要求的流量分配问题，所以有必要在传统算法基础上，构造可行的满足其他条件要求的流量分配算法。

下面介绍三种有条件要求的网络流问题，即边的流量有要求的最大流问题、边的流量有要求的最小费用最大流问题、转运顶点有流量需求的最大流问题。

1.边的流量有要求的最大流问题

网络图中边的流量有要求的最大流问题主要有三种情况：流量不能超过限制值、流量不能低于限制值、流量在一定范围之内。

下面针对三种条件要求，在Ford-Fulkerson算法的基础上，给出边的流量有要求的最大流算法思路。

（1）边的流量不能超过限制值。

算法的思路是，在进行最大流调整分配时，只要将边的原有容量用限制值Z替代即可。因为流量的调整分配必须满足容量约束条件，所以在计算过程中，边的流量不会超过新的容量值，即限制值Z。

（2）边的流量不能低于限制值。

假设要求边(vi,vj)的流量不能低于限制值Z，算法的基本思路如下：

① 先按照标记法寻找从起点x到顶点vi的不饱和链Q1，再按照标记法寻找从顶点vj到终点y的不饱和链Q2，然后确定增流链Q1+(vi,vj)+Q2的调整量，最后对此增流链按照调整公式（9.4）进行流量调整。反复进行，直到边(vi,vj)的流量大于等于限制值Z。

② 继续用Ford-Fulkerson算法对网络图进行最大流分配，但是如果寻找到的增流链中包含边(vi,vj)，并且边(vi,vj)为前向边，那么在确定增流链的调整量时，边(vi,vj)的调整量即为容量减去流量，目的是使边(vi,vj)的流量在限制值Z的基础上有所增加；如果寻找到的增流链中包含边(vi,vj)，并且边(vi,vj)为后向边，那么在确定增流链的调整量时，边(vi,vj)的调整量为流量减去限制值Z，目的是当边(vi,vj)的流量减少时，保证流量不能低于限制值Z。

③ 对以上过程反复进行，直到网络的流量不能增加为止。

（3）边的流量在一定范围之内。

假设要求边(vi,vj)的流量在限制值Z1和Z2之间，算法的基本思路如下：

首先将边(vi,vj)的原有容量用最大限制值Z2替代，然后利用上面第（2）种情况边的流量不能低于限制值的思路，对网络图进行最大流分配即可。

下面通过示例，介绍边的流量有要求的最大流问题。

例9.27　已知某网络图如图9.124所示，边的数据表示容量，试对网络图分配最大流量，其中要求边(v6,v5)的流量在8和10之间。

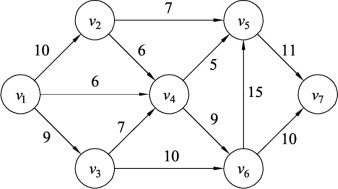
图9.124

解　如果不考虑边(v6,v5)之间的流量要求，直接用Ford-Fulkerson算法即可，针对边(v6,v5)的流量要求，需要利用前面讨论的算法求解。求解步骤如下：

（1）将边(v6,v5)的流量限制值用Z1和Z2表示，即Z1=8，Z2=10，给网络图一个初始的零流，同时用限制值Z2值10替代边(v6,v5)的原有容量15，如图9.125所示。

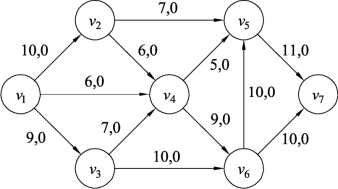
图9.125

（2）因为边(v6,v5)的流量不能小于限制值Z1，所以要先寻找从起点v1到顶点v6的不饱和链。假设寻找到的不饱和链Q1为v1v4v6，其调整量l(Q1)=min{6-0,9-0}=6，再假设寻找到从顶点v5到终点v7的不饱和链Q2为v5v7，其调整量l(Q2)=min{11-0}=11，那么增流链Q1+(v6,v5)+Q2的调整量为min{6,10-0,11}=6。然后利用修改流性质进行流量调整，反复进行，直到边(v6,v5)的流量大于等于限制值Z1，结果如图9.126所示。

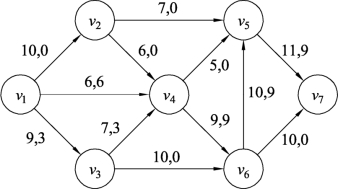
图9.126

（3）继续寻找增流链。假设寻找到的增流链Q为v1v3v6v5v7，链Q中包含边(v6,v5)，并且为前向边，那么链Q的调整量l(Q)=min{9-3,10-0,10-9,11-9}=1。利用修改流性质进行调整，即对网络图用Ford-Fulkerson算法分配最大流，结果如图9.127所示。

（4）对图9.127继续寻找增流链。假设寻找到的增流链Q为v1v2v5v6v7，链Q中包含边(v6,v5)，并且为后向边，那么Q的调整量为

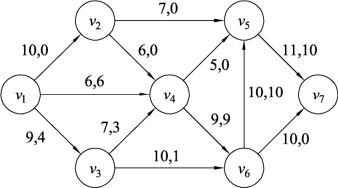
图9.127

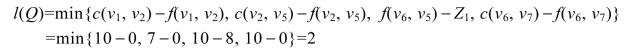
利用修改流性质进行调整，结果如图9.128所示。如此反复进行，最终的最大流如图9.129所示。

在图9.128中，尽管还可以继续找到增流链，但如果继续进行流量调整，就会造成边(v6,v5)的流量小于8，这样就不满足问题给出的要求，所以基于边(v6,v5)的流量在8和10之间的最大流方案如图9.129所示。

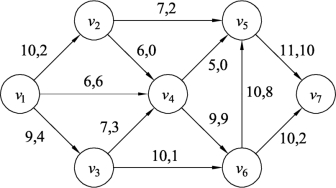
图9.128

图9.129

2.边的流量有要求的最小费用最大流问题

网络图中边的流量有要求的最小费用最大流问题主要有三种情况：流量不能超过限制值、流量不能低于限制值、流量在一定范围之内。下面针对三种条件要求，在Ford-Fulkerson算法的基础上，给出边的流量有要求的最小费用最大流算法思路。(www.daowen.com)

（1）边的流量不能超过限制值。

算法的思路是，在进行最小费用最大流调整分配时，只要将边的原有容量用限制值替代即可。因为流量的调整分配必须满足容量约束条件，所以在计算过程中，边的流量不会超过新的容量值，即限制值。

（2）边的流量不能低于限制值。

假设要求网络图G中边(vi,vj)的流量不能低于限制值Z，算法的基本思路如下：

① 如果边(vi,vj)的流量小于限制值Z，先将边的流量按照最小费用流算法调整到大于等于限制值Z。过程如下：构建伴随网络流f的增流网络Gf，在增流网络Gf中寻找从起点x到顶点vi关于w′的最短路Q1，再寻找从顶点vj到终点y的关于w′的最短路Q2，然后按照最小费用流算法，对网络图G中的增流链Q1+(vi,vj)+Q2的流量进行调整。反复进行，直到边(vi,vj)的流量大于等于限制值Z。

② 按照最小费用流算法规则，继续构建伴随网络流f的增流网络Gf，但针对边(vi,vj)，构建增流网络的方法为：

如果f(vi,vj)=c(vi,vj)并且f(vi,vj)>Z，则构建一条反向边(vj,vi)，其中c′(vj,vi)=c(vi,vj)-Z，w′(vj,vi)=-w(vi,vj)，目的是保证边(vi,vj)的流量在减少时，不能低于限制值Z。

如果f(vi,vj)<c(vi,vj)且f(vi,vj)=Z，则只构建一条同向边(vi,vj)，其中c′(vi,vj)=c(vi,vj)-f(vi,vj)，w′(vi,vj)=w(vi,vj)，目的是保证边(vi,vj)的流量在限制值Z的基础上只能增加，否则就会低于限制值Z。

如果f(vi,vj)<c(vi,vj)且f(vi,vj)>Z，则需要构建一条同向边(vi,vj)和一条反向边(vj,vi)。针对同向边(vi,vj)，c′(vi,vj)=c(vi,vj)-f(vi,vj)，w′(vi,vj)=w(vi,vj)；针对反向边(vj,vi)，c′(vj,vi)=f(vi,vj)-Z，w′(vj,vi)=-w(vi,vj)，目的是保证边(vi,vj)的流量在限制值Z和容量间变动。

③ 按照最小费用流算法反复进行即可。

（3）边的流量在一定范围之内。

假设要求边(vi,vj)的流量在限制值Z1和Z2之间，算法的基本思路如下：

首先将边(vi,vj)的原有容量用最大限制值Z2替代，然后用上面第2种情况边的流量不能低于限制值的思路，对网络图进行最小费用最大流分配即可。

下面通过示例，介绍边的流量有要求的最小费用最大流问题。

例9.28　已知某网络图如图9.130所示，边的数据表示容量和费用，试对网络图分配最小费用最大流，其中要求边(v6,v5)的流量在8和12之间。

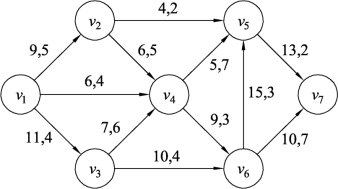
图9.130

解　如果不考虑边(v6,v5)之间的流量要求，直接用最小费用最大流算法即可，针对边(v6,v5)的流量要求，需要利用前面讨论的算法求解。求解步骤如下：

（1）将边(v6,v5)的流量限制值用Z1和Z2表示，即Z1=8，Z2=12，给网络图一个初始的零流，同时用限制值Z2值12替代边(v6,v5)的原有容量15，如图9.131所示。

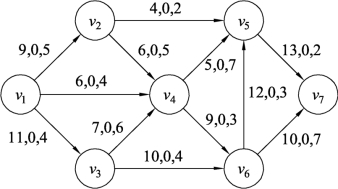
图9.131

（2）因为边(v6,v5)的流量不能小于限制值Z1，那么先将边(v6,v5)的流量按照最小费用流算法调整到大于等于限制值Z1，具体过程省略，结果如图9.132所示。

（3）边(v6,v5)的流量已经满足限制值Z1的要求，对图9.132做增流网络，因为边(v6,v5)的流量不能小于8，所以在增流网络中只能构造同向边(v6,v5)，如图9.133所示。在图9.133中找出从起点v1到终点v7的最短路径为v1v2v5v7，按照最小费用流算法对流量调整，结果如图9.134所示。

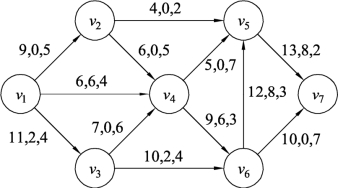
图9.132

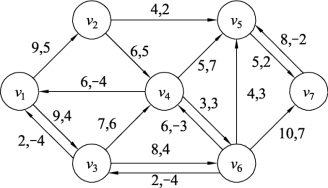
图9.133

（4）对图9.134继续做增流网络，尽管边(v6,v5)为不饱和边，但因为边(v6,v5)的流量不能小于8，所以在增流网络中不能构造它的反向边，结果如图9.135所示。

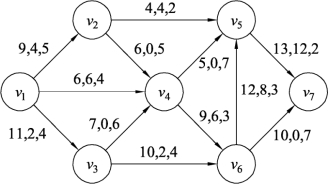
图9.134

（5）在图9.135中找出从起点v1到终点v7的最短路径为v1v3v6v5v7，按照最小费用流算法对流量调整，结果如图9.136所示。进一步做增流网络，因为边(v6,v5)的流量不能小于8，所以增流网络中它的反向边c′(v5,v6)=f(v6,v5)-Z=9-8=1，如图9.137所示。

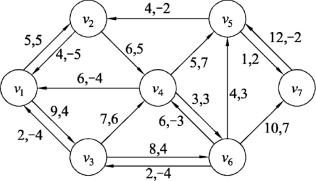
图9.135

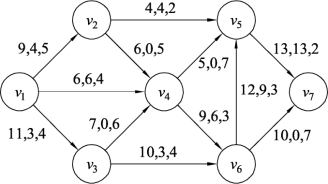
图9.136

（6）在图9.137基础上，按照前面的算法思路反复进行，结果如图9.138所示。对图9.138进一步做增流网络，如图9.139所示。

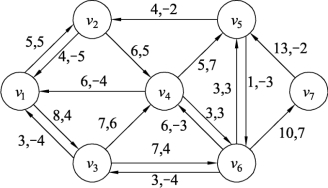
图9.137

图9.139中，不能找到起点v1到终点v7的路径，同时图9.138中边(v6,v5)的流量已经在8和12之间，所以图9.138就是边(v6,v5)的流量在8和12之间的最小费用最大流。

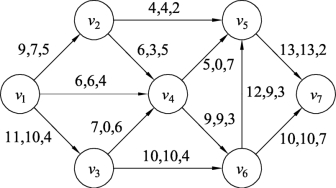
图9.138

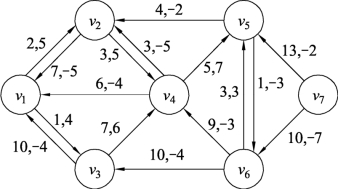
图9.139

特别提示

通过上面的示例，简单地验证和说明了基于Ford-Fulkerson算法，对边的流量有要求的最大流问题以及最小费用最大流问题。对有同类约束条件的流量分配问题，可以进行相应的应用，但有许多问题尤其是流量的不确定问题，需要进行更加完善的处理。